The difference of two squares is easily factored: We have,
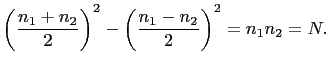
Since ![]() and
and ![]() are both odd,
are both odd,
![]() and
and
![]() are integers.
are integers.
![]()
Note that
![]() hence we can always choose
hence we can always choose ![]() and
and
![]() Then
Then
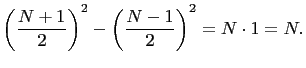
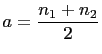 and
and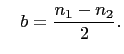
Since
![]() If
If ![]() ,
, ![]() , then
, then ![]() for some positive integers
for some positive integers ![]() and
and ![]() ,
, ![]() . Therefore
. Therefore
Example:
![]() Therefore
Therefore
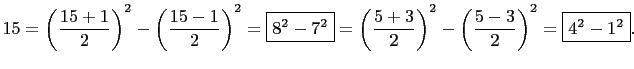
Example: ![]() . So
. So
![]() Therefore
Therefore
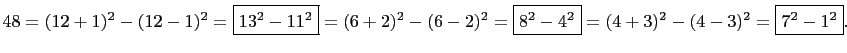
The only positive integers that can not be written as the
difference of two positive integer squares are exactly ![]() , and
those integers
, and
those integers ![]() such that
such that
![]() divides
divides ![]() (that is,
(that is,
![]() ).
).
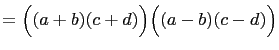 |
||
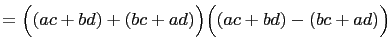 |
||
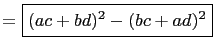 |
||
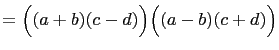 |
||
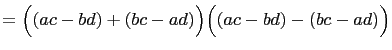 |
||
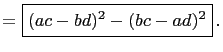 |
Example:
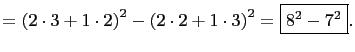 |
||
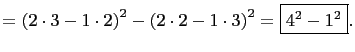 |
Example: Solving the equation
![]() in relatively prime positive integers.
in relatively prime positive integers.
Solution: We know that if ![]() and
and ![]() are
relatively prime and
are
relatively prime and
![]() then one of
then one of ![]() and
and ![]() is odd.
Without loss of generality let
is odd.
Without loss of generality let ![]() be an odd positive integer.
Then there exists relative prime odd positive integers
be an odd positive integer.
Then there exists relative prime odd positive integers ![]() and
and
![]() ,
, ![]() , such that
, such that
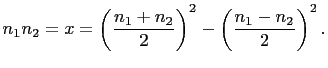
Set
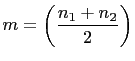 and
and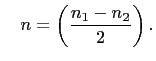
Thus, from equation (45),
From whence
where
From equation (45) we have the inequality,
Compare equation (45) to the Fibonacci identity (
another special case of Brahmagupta's identity. Set ![]() in equation (46) and note that
in equation (46) and note that
![]() ),
),
Similarly Fibonacci's identity can easily be derived
straightforwardly. Set ![]() That is, we will factor each sum
of two squares into Gaussian numbers. Hence
That is, we will factor each sum
of two squares into Gaussian numbers. Hence
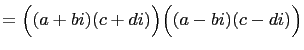 |
||
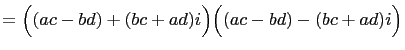 |
||
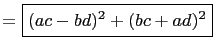 |
||
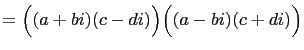 |
||
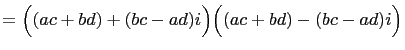 |
||
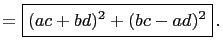 |
This identity implies Cauchy's inequality for reals in two dimensions,
In the Fibonacci identity, set
Similarly, the Diophantus identity (45), set