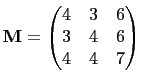
The 120 degree triangle preserving matrix
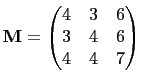
we found in the previous section, can be transformed into four 60 degree triangle preserving matrices. To do so, we will need the following identity,
We have
![]() . Then using
. Then using
![]() ,
,
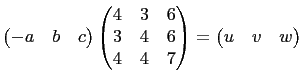
where
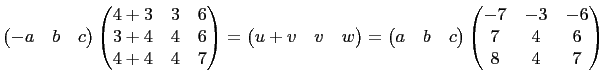
where
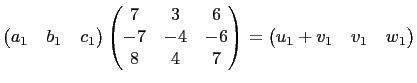
where
Let
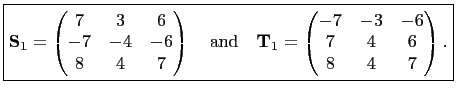
Then, clearly,
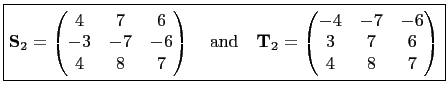
are also 60 degree triangle preserving matrices.
For example, since
![]() ,
,
where
Download these 3 sections in pdf form. triples8.pdf