


Next: 60 degree triangle preserving
Up: 120 degree primitive triples,(a,b,c),
Previous: 120 degree primitive triples,(a,b,c),
Contents
Let
From table (7), set
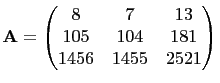
and
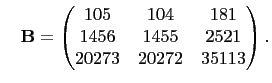
So solving for
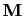 in the matrix equation
in the matrix equation
we find that
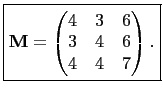 |
(39) |
If
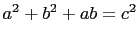 then
then
where
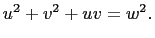 And
And
where 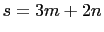 and
and 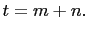 So, if
So, if
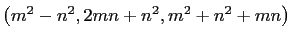 is a primitive triple,
is a primitive triple, 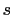 and
and 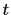 are, relatively prime, positive integers,
are, relatively prime, positive integers, 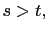 where,
where,
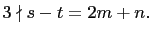 That is,
That is,
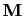 takes a primitive triple
and outputs a primitive triple.
takes a primitive triple
and outputs a primitive triple.
Note that 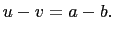 For example.
For example.
If 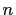 is a positive integer then
is a positive integer then
where
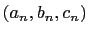 is the
is the 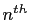 solution to the primitive 120
degree triangle
solution to the primitive 120
degree triangle
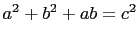 such that
such that
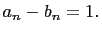



Next: 60 degree triangle preserving
Up: 120 degree primitive triples,(a,b,c),
Previous: 120 degree primitive triples,(a,b,c),
Contents
f. barnes
2008-04-29


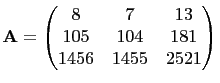 and
and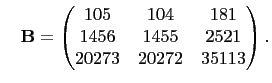
![]() then
then
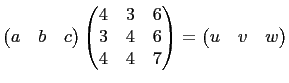
![]() For example.
For example.
![]() is a positive integer then
is a positive integer then