

Next: A 120 degree triangle
Up: Pythagorean Triples, etc.
Previous: 120 degree and 60
Contents
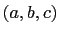 is a primitive solution in positive integers to the 120
degree equation
is a primitive solution in positive integers to the 120
degree equation
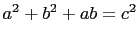 if and only if there exists
relatively prime, positive integers
if and only if there exists
relatively prime, positive integers 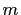 and
and 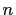 ,
, 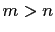 ,
,
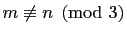 such that
such that
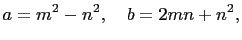 and and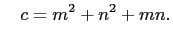 |
(38) |
Finding solutions where a-b=1
(We'll need these first four recursive solutions to find
the first matrix.)
Let
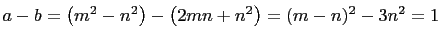 , a
Pell equation. Hence, solutions are
, a
Pell equation. Hence, solutions are
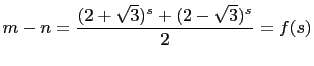
and
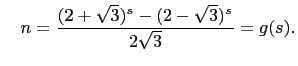
Then
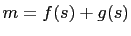 and
and 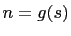 . Thus
. Thus
Examples
Table 7:
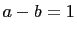 .
.
| s |
f(s) |
g(s) |
m |
n |
a |
b |
c |
| 1 |
2 |
1 |
3 |
1 |
8 |
7 |
13 |
| 2 |
7 |
4 |
11 |
4 |
105 |
104 |
181 |
| 3 |
26 |
15 |
41 |
15 |
1456 |
1455 |
2521 |
| 4 |
97 |
56 |
153 |
56 |
20273 |
20272 |
35113 |
Subsections



Next: A 120 degree triangle
Up: Pythagorean Triples, etc.
Previous: 120 degree and 60
Contents
f. barnes
2008-04-29
![]() is a primitive solution in positive integers to the 120
degree equation
is a primitive solution in positive integers to the 120
degree equation
![]() if and only if there exists
relatively prime, positive integers
if and only if there exists
relatively prime, positive integers ![]() and
and ![]() ,
, ![]() ,
,
![]() such that
such that
![]() , a
Pell equation. Hence, solutions are
, a
Pell equation. Hence, solutions are
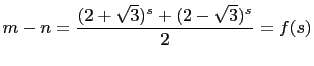 and
and