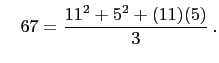If given a primitive triangle
![]() , we know that one
of
, we know that one
of ![]() and
and ![]() is equal to
is equal to ![]() and the other equals
and the other equals
![]() where
where ![]() and
and ![]() are relatively prime, positive
integers,
are relatively prime, positive
integers, ![]() , and
, and
![]() . But, how do we determine which
of
. But, how do we determine which
of ![]() and
and ![]() equals
equals ![]() ?
?
![]() . Either
. Either ![]() or
or
![]() . If
. If ![]() then
then
![]() .
Therefore
.
Therefore ![]() .
.
![]()
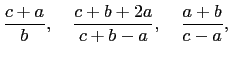 and
and 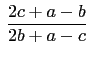
(each fraction reduced to lowest terms) is equal to
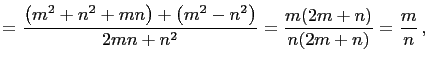 |
||
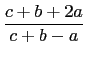 |
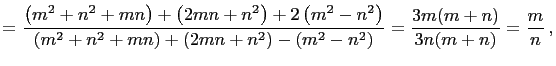 |
|
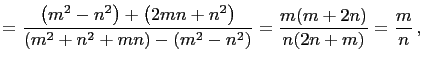 |
||
and 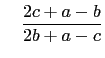 |
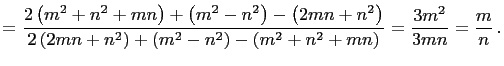 |
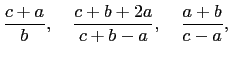 and
and 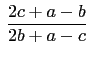
(each fraction reduced to lowest terms) is equal to
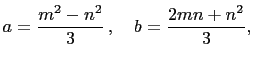 and
and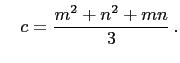
Then
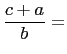 |
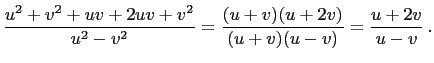 |
|
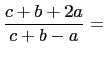 |
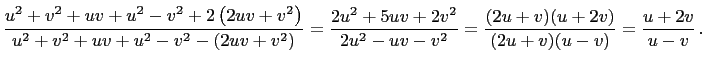 |
|
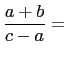 |
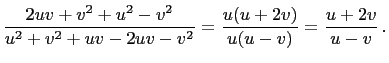 |
|
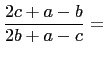 |
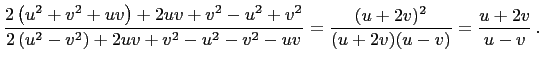 |
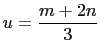 and
and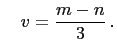
Hence, we have,
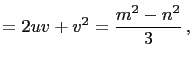 |
||
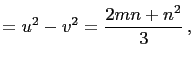 |
||
| and |
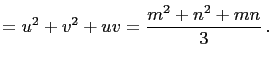 |
![]() is a primitive 120 degree triangle.
is a primitive 120 degree triangle.
![]() . Therefore
. Therefore ![]() . So,
. So,
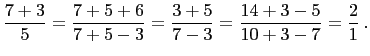
Hence ![]() ,
,
![]() , and
, and
![]() .
.
![]() is primitive.
is primitive.
![]() .
Therefore
.
Therefore ![]() . Thus
. Thus
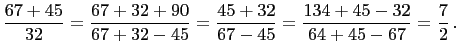
Hence
![]() ,
,
![]() , and
, and
![]() .
.
![]() is a primitive 120 degree triangle.
is a primitive 120 degree triangle.
![]() . Therefore
. Therefore ![]() . So,
. So,
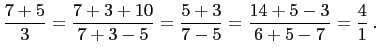
Hence
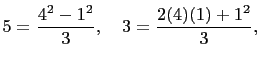 and
and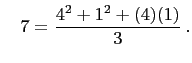
![]() is primitive.
is primitive.
![]() .
Therefore
.
Therefore ![]() . Thus
. Thus
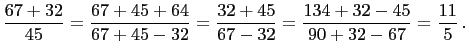
Hence
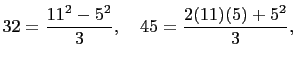 and
and