Tangent Handrailing Planes and Angles
Lower Tangent Plane Slope Angle = 50°
Upper Tangent Plane Slope Angle = 40°
Angle negotiated by Handrailing = 60°
(Angle between Tangents in Plan View = 120°)
Tetrahedron modeling the Lower (50°) Tangent Plane Angles
... not seen on the developed drawing to the scale of the model, a downsized version
of this tetrahedron has a vital role to play and will make an appearance later.
Development of the Tetrahedron
Lower Tangent Plane Slope Angle = r5P = 50°
Lower Tangent Plane Plan Angle = dd = 76.73958°
Angle produced on Oblique Plane by trace
of Lower Tangent Plane = r4P = 8.47866°
Dihedral Angle measured between the
Level (Plan View) Plane and the Oblique Plane = R1 = 50.76055°
Dihedral Angle measured between the
Lower Tangent Plane and the Oblique Plane = 90° – a5P = 79.76680°

Elevation ... View of 50° Tangent Plane

View of Oblique Plane ... r4P = 8.47866°
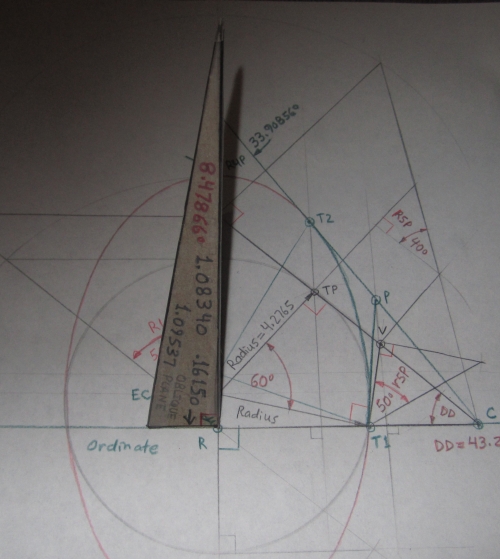
Tetrahedron modeling the Upper (40°) Tangent Plane Angles
... the location of this group of triangles on the drawing is self-evident.
Development of the Tetrahedron
Upper Tangent Plane Slope Angle = R5P = 40°
Upper Tangent Plane Plan Angle = DD = 43.26042°
Angle produced on Oblique Plane by trace
of Upper Tangent Plane = R4P = 33.90856°
Dihedral Angle measured between the
Level (Plan View) Plane and the Oblique Plane = R1 = 50.76055°
Dihedral Angle measured between the
Upper Tangent Plane and the Oblique Plane = 90° – A5P = 55.66480°

Elevation ... View of 40° Tangent Plane

View of Oblique and Section Planes
Vertex of the Oblique Plane Triangle ... Angle R4P = 33.90856°
Angle R1 = 50.76055° on the Section Plane is the dihedral angle
measured between the Plan View (Level) Plane and the Oblique Plane.

Views of the Tetrahedra modeling the Tangent Plane Angles
juxtaposed along their respective Section Planes
... these tetrahedra appear on the development on a smaller scale (see below).
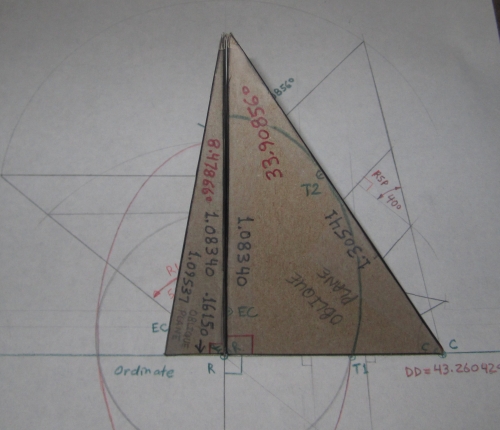
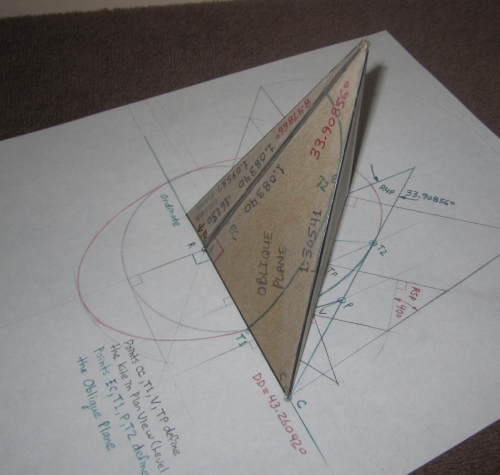
Pentahedron modeling the Tangent Plane Angles
... the tetrahedron of the upper (40°) tangent plane angles with scaled
down juxtaposed tetrahedra extracted from the lower right hand corner.
Development of all Planes and Angles
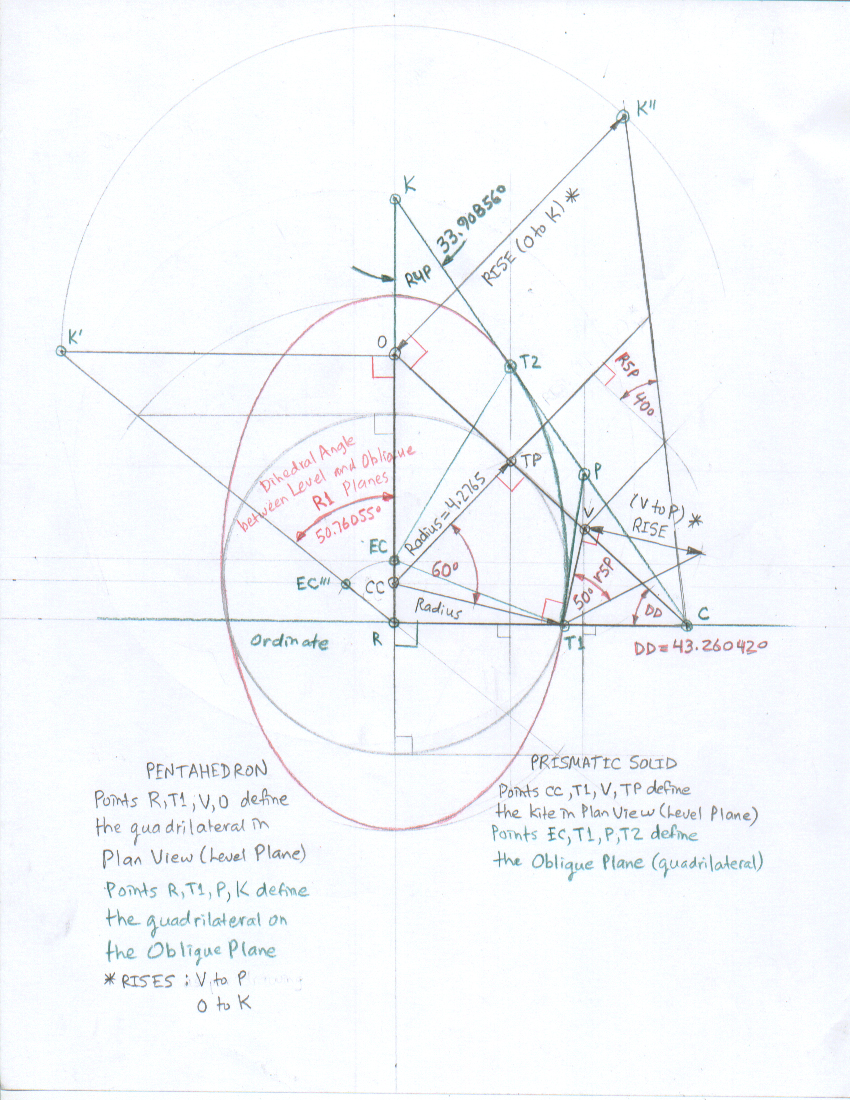
Development of Pentahedron extracted from the drawing above

View of Oblique Plane ... line K P is tangent to the ellipse at point T2.
Angle K P T1 is the "Angle between Tangents"; the angle
produced on the oblique plane by the traces of the tangent planes
= 180° – (r4P + R4P) = 180° – (8.47866° + 33.90856°) = 137.61278°.
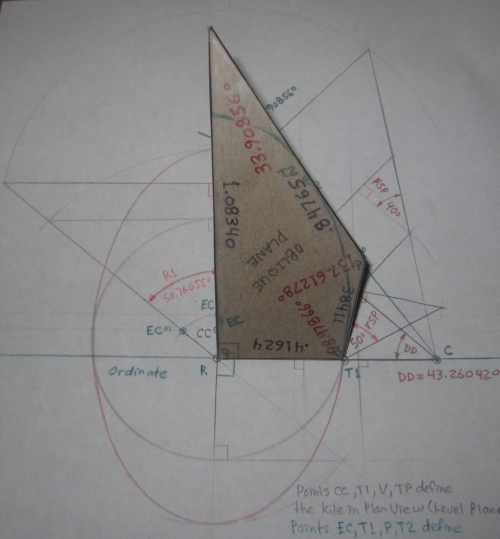
View from Corner at Point of Tangency (T1)
Note that the dihedral angle measured between the lower
tangent plane and the oblique plane is 90° + a5P = 100.23320°.

Views of the Tangent Planes intersecting along plumb line V P


Juxtaposed Tetrahedra modeling the Tangent Plane Angles
... the scaled down pair of tetrahedra removed from the lower right hand corner
of the upper tangent plane tetrahedron to produce the pentahedron above.
The tetrahedra are shown sitting on the construction of the twist angles
(the dihedral angles measured between the oblique plane and the tangent planes).
Development of the Juxtaposed Tetrahedra

View of the Oblique Plane
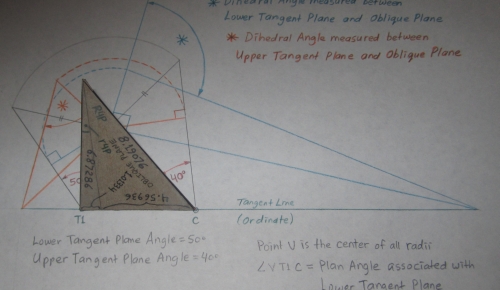
Views of the Tangent Planes
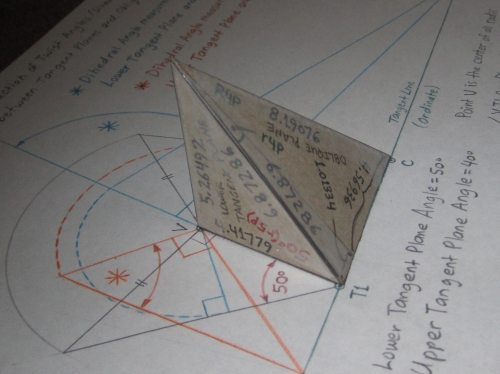

Prismatic Solid (Post-Type Model)
... beginning with the pentahedron, raise a plumb plane through
points TP and CC, and a plumb plane through points T1 and CC.
Development of all Planes and Angles
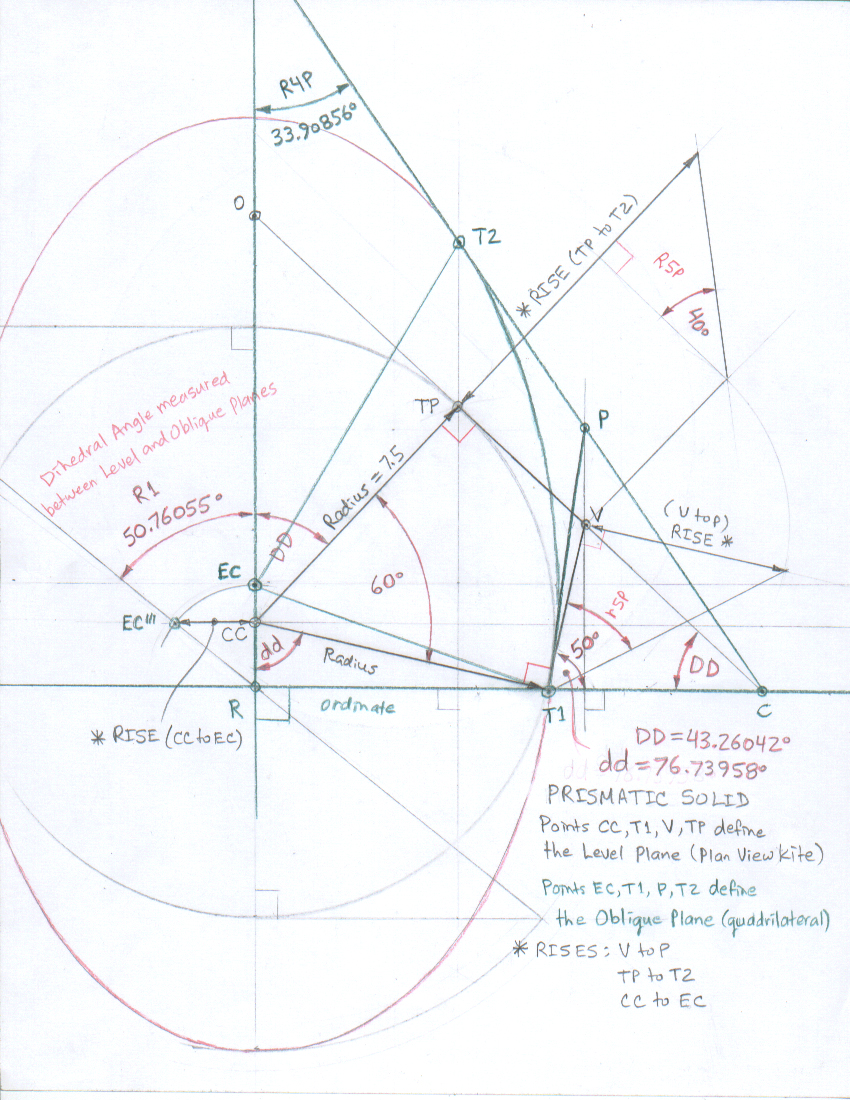
Development of Prismatic Solid extracted from the drawing above

View of Oblique Plane

View of Corner at Point of Tangency (T1)
As in the pentahedron, the dihedral angle measured between the
lower tangent plane and the oblique plane is 90° + a5P = 100.23320°.

View of plumb line through Points CC and EC

View of the Tangent Planes and plumb line through Points V and P

View of plumb line through Points TP and T2
(T2 is the second Point of Tangency on Oblique Plane)

Juxtaposed Prismatic Solid and Tetrahedra modeling the Tangent Plane Angles
... the dihedral angles between the oblique plane and tangent planes may be measured on any of the solids.
These dihedral angles are the twist angles seen on the handrailing layout on the end grain of the block.
All of the solids above are found in the developed drawing and describe the same group of planes.
View of the Oblique Plane
... it's always the same surface, angled at 50.76055° with respect to level.
