Diagram and formula for the cosine of the Backing Angle
Diagram and formula for the sine of the Backing Angle
Algebraic solution of the formula for the sine of the Backing Angle
Diagram and formula for the tangent of the Backing Angle
3D Model ... Interlocking Tetrahedra illustrating the tangent of the Backing Angle
Example calculation of the Backing Angle: Regular Octagonal Gazebo
Formula for Tangent of Backing Angle
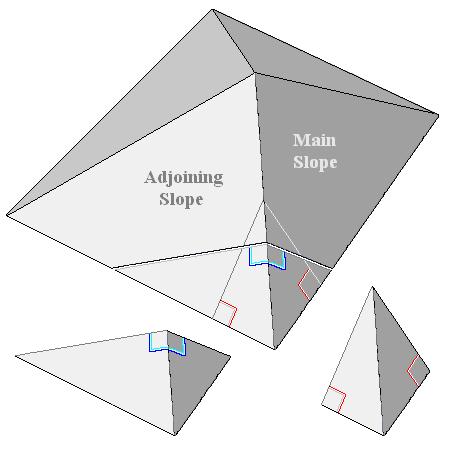
Tetrahedra of Common Pitch Angles (right) and
Backing Angles (left) extracted from the Hip Roof.
Dihedral Angle: The angle measured between two planes
|
To measure a dihedral angle, select a
point on the arris
or line of intersection between the planes.
Project lines at right angles from the working point along the surface of each plane of interest. The dihedral angle is the angle measured between these two lines. The dihedral angle constructed in the diagrams below is the complement of the Backing Angle. |
Trigonometric Scaling
Lengths with respect to Hip Run = 1
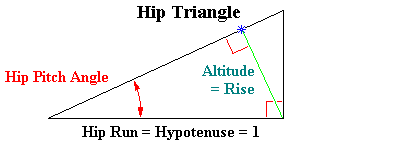
|
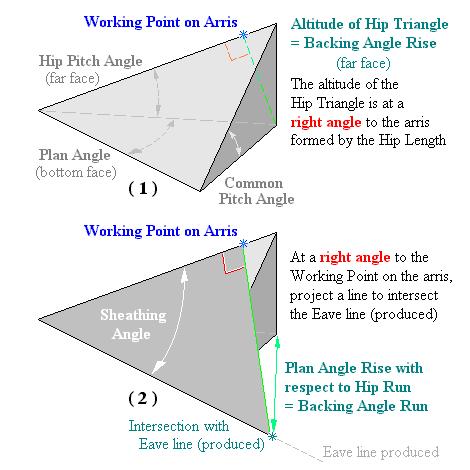
If the Hip Run = 1, the altitude of of the Hip Triangle is opposite the Hip Pitch Angle
and the run forms the hypotenuse.
Altitude/Run = Altitude/Hypotenuse = Opposite/Hypotenuse = sin Hip Pitch Angle Opposite/1 = sin Hip Pitch Angle Opposite = 1 × sin Hip Pitch Angle = Altitude = Backing Angle Rise |
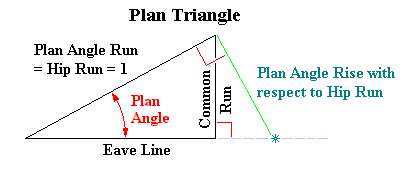
|
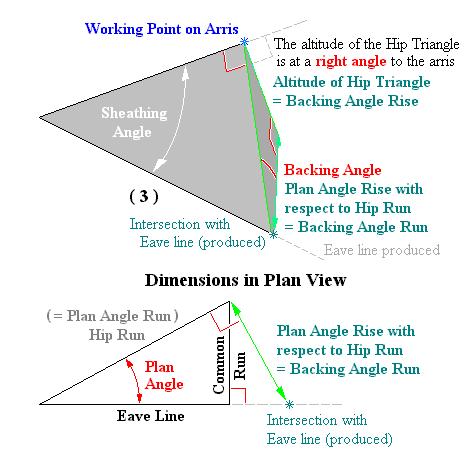
If the Hip Run = 1, the Plan Angle Run = 1. With respect to the Plan Angle:
Rise/Run = Rise/1 = Opposite/Adjacent = tan Plan Angle Opposite/1 = tan Plan Angle Opposite = 1 × tan Plan Angle = Backing Angle Run With respect to the Backing Angle: Backing Angle Rise/Backing Angle Run = Opposite/Adjacent = tan Backing Angle Backing Angle Rise/Backing Angle Run = Hip Triangle Altitude/Plan Angle Rise Backing Angle Rise/Backing Angle Run = sin Hip Pitch Angle/tan Plan Angle tan Backing Angle = sin Hip Pitch Angle/tan Plan Angle Taking the arctan of both sides of the equation: Backing Angle = arctan (sin Hip Pitch Angle / tan Plan Angle) |
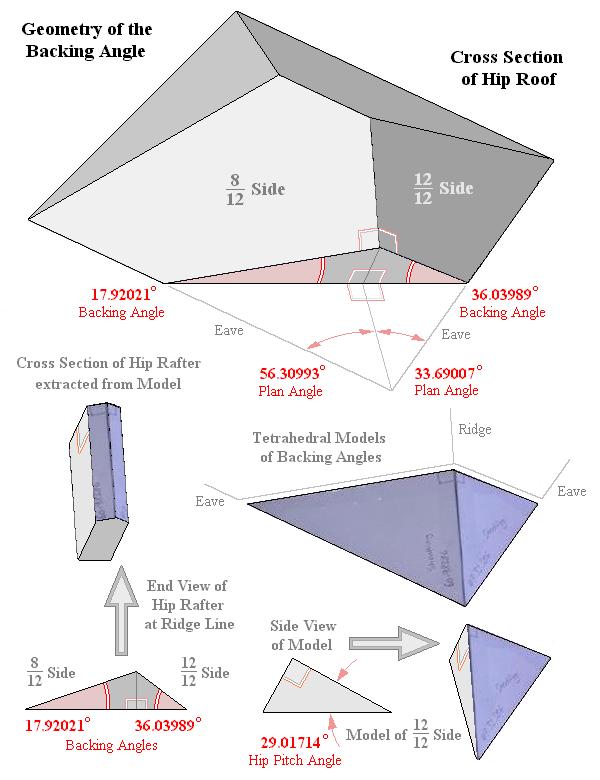
Hip Rafter: 8/12 and 12/12 Slopes
Eaves intersect at 90° in Plan
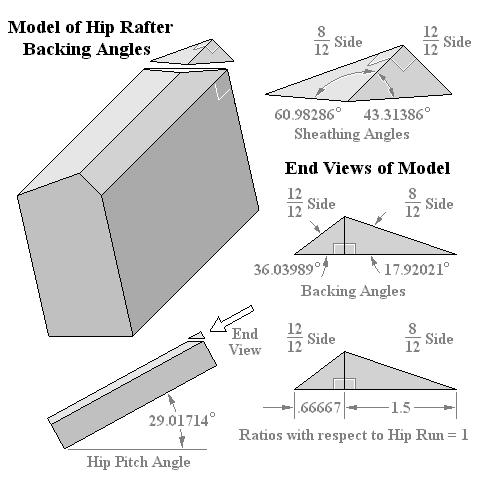
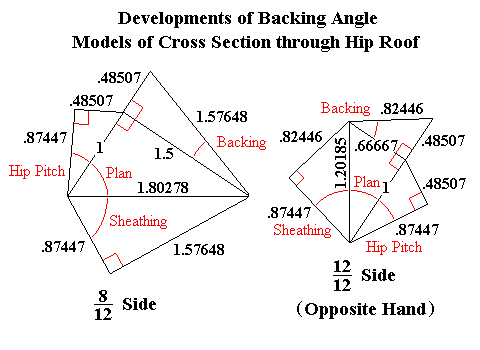

3D Model of Backing Angles

View of Sheathing Angles about the Ridge Line