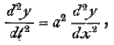
If we suppose the rod infinitely thin we may neglect κ altogether. The differential equation (6') then reduces itself to
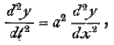
the ordinary equation for a perfectly flexible string ; and (14) gives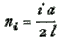 
, the value found before.
But if we consider the rod as very thin, without being infinitely thin, so that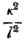 
is a very small fraction, the value (14) will be applicable to the case of a metallic string or wire. In this case, neglecting the square of 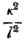, and assuming the section of the wire to be a circle with radius r, so that 
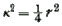, we find 
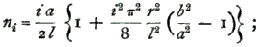hence if we put 
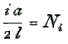(the number of vibrations calculated on the supposition of infinite thinness or perfect flexibility2), and put for b2 and a2 their values (art 178), we have
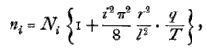
which gives what is called the correction for rigidity.
This correction may be put in another form thus : from (14) we have
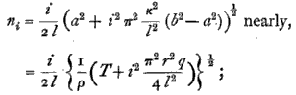
so that for a given value of i, that is, for a tone of given order , the number of vibrations corresponding to any actual tension T may be calculated as if the string were perfectly flexible, by substituting for T a fictitious tension
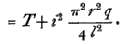
The term thus added is sensibly independent of T, since l (the actual length between the bridges) is constant, and r is sensibly invariable, at least for moderate variations of T. If the tension be supplied by a weight W, the W=Tω. Suppose Q is the weight which would double the length of the string if the law of extension held good indefinitely, then Q=qω. Hence the fictitious weight to be substituted in calculation for the actual weight is
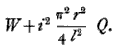
It would be difficult to calculate the value of the added term 'a priori, because the values of the very small ratio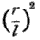 
and of the very large weight Q, could hardly be obtained with sufficient accuracy ; but it is easily ascertained experimentally by comparing the tones produced by two different weights. The tones corresponding to other values of W can then be calculated, and they are found on trial to agree very exactly with those actually produced...
2 Strickly speaking, the supposition of infinite thinness ought to be distinguished from perfect fflexibility. We can imagine a thick string of which only the central infinitely thin axis should resist extension or contraction. Such a string might be regarded as perfectly flexible. But the interia of the outer parts would introduce the termin the differential equation, though the term
, which arises from the resistance of the outer parts to extension or contraction, would disappear. But the strings used for musical purposes never approximate to this character, though the converse arrangement is common, e.g. in guitar strings made by winding fine wire upon a silk core.
The supposition of permanent tension, with fixed terminal faces, leads to much more complicated equations, but they may be treated in an approximate manner in the only case of practical importance, namely, that in which the thickness of the rod is very small compared with its length. The result may then be considered as giving the correction for rigidity for a wire, or for a long and thin lamina, not stretched over bridges, but firmly clamped at the ends.
We may take in this case the equations (7), (9), and (11), as in Arts. 179 and 180. But we shall suppost the term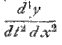 
in (6') to be neglected, so that instead of (9') we get the simpler form 
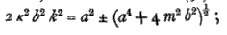and therefore , since α2 and -β2 are the two values of k2, we may write the value of α2 thus :
and β2 will be given by changing +1 into -1 in the last term of the numerator.
Now in the case of a metallic wire or lamina,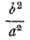 
is a large number (see Art 178) since T is small compared with q. But 
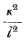is very small ; and the legitimacy of the following approximation depends upon the assumption that 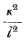is so small that 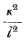* 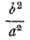is also very small. From this assumption it follows that α l is very large, since α2 l2 is expressed by a fraction in which the numerator is >2 and the denominator is the small fraction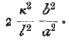 
Now the terminal conditions are y = 0,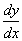 
= 0, at both ends, and from these, proceeding as in Art. 189, we find from equation (11)
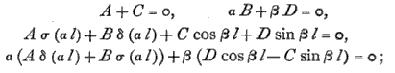
and hence, eliminating A, B, C, D, and reducing by means of the identity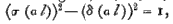 
we find, finally,
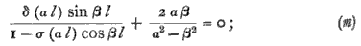
and if in this equation the values of α and β given above were introduced, we should obtain an equation in m, of which the roots would be the values of m1, m2, &c.
Now the values of α2, β2 give, as will be found at once without difficulty,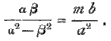 
Also, since α l is very large, we have, neglecting 
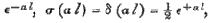and the equation (m) becomes
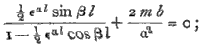
or εαl being again neglected,
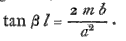
Now the value of β2 gives
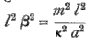nearly
(by developing the binomial as far as the second term) ; hence
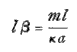nearly.
But the number of vibrations in a unit of time is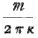 
; and since the case differs very little from that of an infinitely thin string, this number differes very little from 
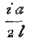, so that 
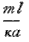differs very little from iπ, or βl = iπ +θ, where &theta is very small ; hence 
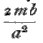= tanβl = tanθ is very small ; and we may take 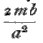= θ, and therefore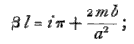 
and, equating this to 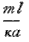, we have
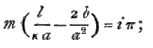
or, introducing the subscript index to distinguish the different values of m,
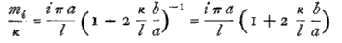nearly.
Let ni be the number of vibrations, in a unit of time, of the ith tone, and Ni the number calculated on the supposition of infinite thinness ; then
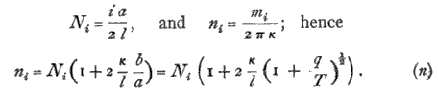
Comparing this with the corresponding expression deduced in Art. 184 on the supposition that the directions of the terminal faces were free, viz,
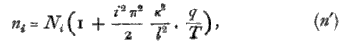
we see that they differ essentially, especially in this respect, that in the case (n) of fixed faces the pitch of all the component tones is raised, by the rigidity, through the same interval, so that they do not cease to form a harmonic series ; whereas in the other case (n') each tone is raised through a greater interval than the next lower one, and the series is therefore no longer strictly harmonic.
An expression equivalent to (n), and obtained by nearly the same process, was given by Seebeck1, and found by him to agree with the experiment when the ends of the wire were clamped.
In the case of a wire stretched over bridges, the form (n') has been found to agree with experiment, in the manner mentioned at the end of Art. 184. But the deviation of the upper tones from the harmonic scale is probably too small to be made sensible to the ear.
1 [In a memoir of the transverse vibrations of rods. (Abhandlungen d. Math. Phys. Classe d. K. Sa"ches. Gesellschaft d. Wissenschaften. Leipzig, 1852.)]