Two travelers, Al and Bert, have independent accelerated motions along a straight line

Derivation of the rate of an accelerating clock relative to an accelerating observer

Two travelers, Al and Bert, have independent accelerated motions along a straight line. Their motions may be plotted on a spacetime diagram from the point of view of a single inertial reference frame that we’ll call the “earth” reference frame.

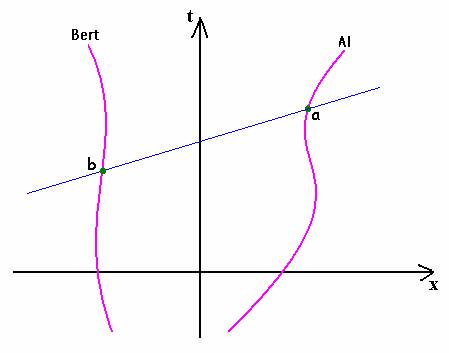
When Al reaches point a of his world-line, he wishes to compare the rate of Bert’s clock with his own clock. The blue line is the locus of all points that are considered to be simultaneous with event a from the point of view of the inertial frame that is instantaneously co-moving with Al. Thus, at the instant Al reaches point a he would consider Bert’s clock to read the value that it has at point b on Bert’s world-line. [See comments on last page.]

Let

= the reading of Al’s clock at event a,

= the reading of Bert’s clock at event b.

Let the symbols x and t denote coordinates of events as measured in the earth frame.

The world lines of the travelers may be defined in the earth frame by certain functions and . Point a of Al’s world line would have earth coordinates and . Likewise, point b on Bert’s world line has earth coordinates and .

We may derive a relationship between and by considering the figure below.

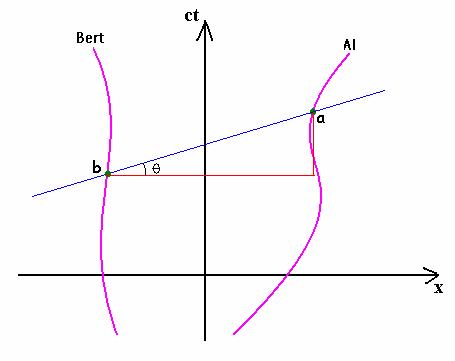
From the right triangle we have

But, it is well known that the tilt of the line of simultaneity in the spacetime diagram is determined by

where

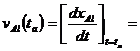the velocity of Al with respect to the earth frame at point a.

So, (1)

Rearranging gives

. (2)

This relationship allows one, in principle, to determine the value of for a given value of since the functions and are presumed to be known. (However, for general functions, it may not be possible to actually solve explicitly for . Nevertheless, the above relation does define implicitly and could always be determined by this relation using numerical techniques.)

In order for Al to compare his clock rate with Bert’s clock rate, he must move a little along his world line and compare how much Bert’s clock increases to how much his own clock increases. So, we consider the following diagram

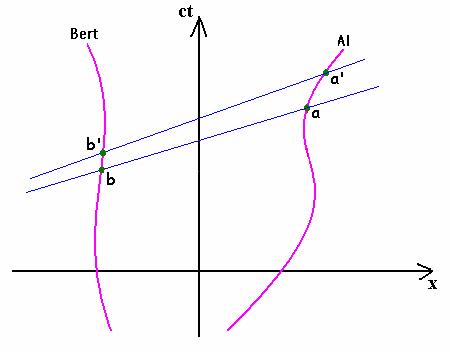
As Al moves from point a to point a', his own clock will advance from to . He will consider event b to be simultaneous with event a and event b' to be simultaneous with event a'. So, as his clock advances from to , he would “observe” Bert’s clock to advance from to . Note that the line of simultaneity through a' does not have the same slope as the line of simultaneity through a due to the acceleration of Al (which causes his velocity relative to the earth frame to change in going form a to a').

Now, the connection between and will have exactly the same form as equation (2). Namely,

(3)

Subtracting equation (2) from equation (3) yields

(4)

We consider the events a and a' to be infinitesimally close so that we may write

and (5)

Likewise,

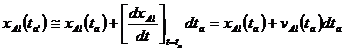(6)

which is accurate to first order in .

Likewise,

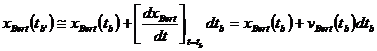(7)

Also,

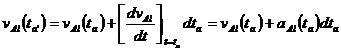(8)

Here, is the acceleration of Al relative to the earth frame at event a.

Substituting (5), (6), (7), and (8) into (4), simplifying, and keeping only terms up to first order in and yields

(9)

Let

= the increase in Al’s clock between events a and a' =

= the increase in Bert’s clock between events b and b' =

These are related to the time increments and in the earth frame according to the well-known time dilation relations

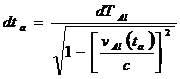and 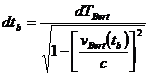(10)

Substituting (10) into (9) and rearranging yields

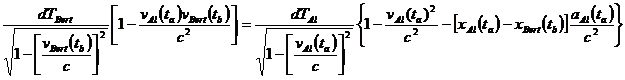
(11)

The rate of Bert’s clock as observed by Al is the ratio . Rearranging the above equation gives

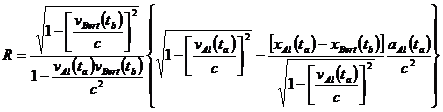(12)

This expresses the rate of Bert’s clock as observed by Al’s clock in terms of the velocities and positions of Al and Bert relative to the earth frame at the events a and b and also in terms of the acceleration of Al relative to the earth frame. We may also express the result in terms of the acceleration that Al “feels”. This is his acceleration relative to the instantaneously co-moving inertial frame. Denote this co-moving acceleration by g. The relationship between and g is known to be

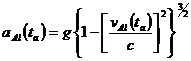(13)

(See, for example, Sections 3.7 and 3.8 of D’Inverno’s Introducing Einstein’s Relativity.)

Thus, the rate of Bert’s clock as observed by Al at a may be written

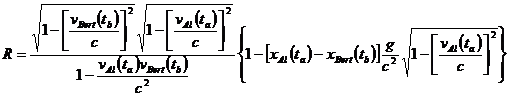(14)

Furthermore, the distance, D, between Al and Bert as measured in the co-moving frame is

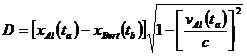(15)

So, R may be written

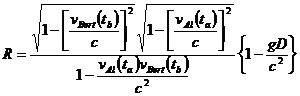(16)

Finally, using the velocity addition formula we may write the velocity of Bert relative to Al (as measured in the co-moving frame) as

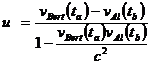(17)

Using (17) it can be shown that the quantity is identically equal to the complicated factor in front of the curly brackets in equation (16). Hence, we may write (16) as

(18)

One may check that the signs work out correctly if we adopt the following conventions:

D is always taken to be positive. g is positive if Al’s acceleration is away from Bert’s location and negative if Al’s acceleration is toward Bert’s location. By “Bert’s location”, we mean, of course, the location as determined in the inertial frame that is instantaneously co-moving with Al.

-------------------------------------------

It is interesting to try to interpret (18) heuristically in terms of the equivalence principle and GR. Suppose that Al says that he is “always at rest” and that the “g-force” that he experiences at some instant is due to a (time varying) uniform gravitational field of magnitude g. The factor in the curly brackets is the well-known time dilation factor for clocks at rest in a uniform gravitational field (at least for the case where ). The factor is an additional time dilation factor due to the motion of Bert relative to Al.

-----------------------------------------

Comments:

Our derivation presumes a specific choice of how Al determines which particular reading

of Bert’s clock is simultaneous with a particular reading of his own clock. We adopted

the “co-moving inertial reference frame” definition:

DEFINITION:  At any particular reading of his own clock, Al is instantaneously at rest

 with respect to some comoving inertial frame.  Observers in this comoving frame can use

 the standard inertial-frame definition of simultaneity to determine the specific instant of

 Bert’s clock that they consider to be simultaneous with the particular reading of Al’s

 clock.  Al (by definition) accepts this particular reading of Bert’s clock to be

 simultaneous with the particular reading of his own clock.

Other definitions of simultaneity for Al could be constructed.  These could lead to different

formulas for the rate of Bert’s clock as “observed” by Al.  It is important to

realize that these different formulas would all be correct for their corresponding

definitions of simultaneity.  They would all yield the same predictions for any time

measurements that have objective, physical significance – such as how two clocks

compare when they meet at the same spacetime point (twin paradox).   This is probably

the reason that such formulas are not found in the standard texts on relativity.  It is much

easier to analyze accelerated clocks from the point of view of some fixed inertial

reference frame rather than from the point of view of one of the accelerating clocks.

 Thus, our derivation is mainly just an interesting academic exercise.

Additional Note:  The final result (18) may be obtained with much less algebra and

without loss of generality by choosing the “earth” frame to be the inertial frame that

happens to be co-moving with Al at event a .  Then, 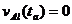 throughout the derivation

and one may obtain (18) immediately from (12).