8. VIBRAÇÃO DE CORDAS E TUBOS

Podemos produzir ondas sonoras excitando o ar por meio de vibrações de corpos elásticos. Os instrumentos musicais são um ótimo exemplo das diversas possibilidades, podendo ser de cordas, de sopro ou de percussão. Nos primeiros são cordas metálicas ou não, feitas vibrar por efeito de pequenos deslocamentos de suas posições de equilíbrio; nos segundos, o corpo vibrante é o ar no interior de um tubo; nos terceiros o corpo vibrante é uma membrana elástica ou um disco metálico. Dependendo do material que constitui o corpo vibrante e de seu estado físico, ou seja, a pressão, a temperatura e a tensão sob as quais se encontra, a freqüência básica de vibração pode variar bastante. A dedução matemática da freqüência emitida por um desses corpos é bastante elaborada e de nível superior ao do público ao qual o presente trabalho se destina. Por essa razão, será apresentada uma forma fenomenológica de deduzir essas freqüências.

8.1. CORDAS VIBRANTES

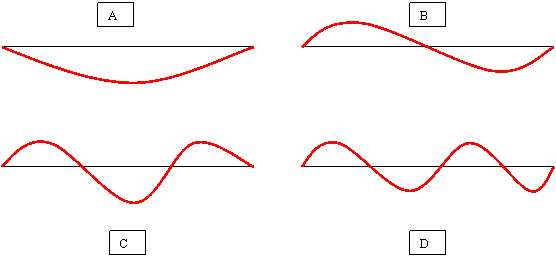
Uma corda metálica ou de material elástico qualquer, esticada e presa em suas extremidades, ao ser deslocada da posição de equilíbrio, pode vibrar de uma infinidade de maneiras diferentes. A diferencia essencial é o comprimento das ondas que se formam entre os dois pontos fixos da corda e a amplitude correspondente. A Figura 8.1 ilustra algumas das possibilidades.

FIGURA 8.1 - ALGUNS MODOS DE VIBRAÇÃO DE UMA CORDA

Observamos que na forma de vibrar A, o comprimento de onda l da vibração é igual ao dobro do comprimento l da corda, isto é, l = l/2. Da mesma forma, no caso B, l = l, no caso C, l =3l/2 e, no caso D, l = 2l. No caso geral temos que a corda pode vibrar com o comprimento de onda dado por l = n l_n /2. onde n cobre o conjunto de todos os números inteiros positivos. Acontece que a amplitude de vibração é tanto menor quanto menor for o comprimento de onda, de modo que ao pinçarmos uma corda iremos ouvir apenas as freqüências correspondentes aos maiores comprimentos de onda. Essas freqüências são os harmônicos emitidos pela corda vibrante. O harmônico de maior comprimento de onda, ou seja, l = 2l, chama-se harmônico fundamental. As freqüências emitidas pela corda vibrante em correspondência a cada harmônico são dadas pela relação

f_n = nv/2l

e a velocidade de propagação v é dada por

v= (T/r)^1/2

onde T é a força de tensão à qual a corda está submetida e r sua densidade linear, ou seja, a massa por unidade de comprimento. Assim, resulta que as freqüências possíveis de uma corda vibrante são dadas por

f_n = n(T/r)^1/2/2l

e os correspondentes comprimentos de onda são dados por

l = n l_n /2

o número n tomando todos os valores de 1 até um valor arbitrariamente grande.

A amplitude de cada harmônico diminui ao se aumentar a freqüência, sendo seu valor inversamente proporcional ao quadrado de n.

Na realidade, se a corda for excitada a uma distância d de uma sua extremidade e deslocada inicialmente de uma quantidade h de sua posição de equilíbrio, essas amplitudes são dadas por

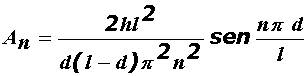
EXEMPLO: Qual deve ser o comprimento de uma corda de aço (densidade linear de 0,01 kg/m) submetida a uma tensão de 3500 N, se a freqüência fundamental que essa corda emite é o de 435 Hz?

Calculemos a velocidade do som na corda especificada. Essa velocidade é dada por

v= (T/r)^1/2= (3500 / 0,01)^1/2 = 591,61 m/s

A freqüência fundamental é dada por f₁ = v/2l, ou seja, o comprimento da corda deve ser l = v/2f₁ = 591,61/ 2x435 = 0,68 m, ou seja, 68 cm. Se aumentarmos o comprimento dessa corda, obteremos um som mais grave (freqüência menor) e, se diminuirmos o comprimento, obteremos um som mais agudo (freqüência maior).

Esse exemplo pode ser desenvolvido com facilidade utilizando seu Laboratório Virtual.

EXEMPLO: Uma corda vibrante tem comprimento de 30 cm e o som fundamental que ela emite é de 870 Hz. Qual a velocidade de propagação das ondas na corda?

O comprimento de onda do som fundamental é duas vezes o comprimento da corda. No caso então, l = 2x30 = 60 cm = 0,6 m. A freqüência correspondente é dada por f₁ = v/l = v/2l. Logo, a velocidade de propagação das ondas na corda vibrante é v = f₁x2l = 870 x 0,6 = 522 m/s.

[ topo ]

8.2. TUBOS VIBRANTES

Instrumentos sonoros de sopro podem ser constituídos de tubos abertos nas duas extremidades, como é o caso de uma flauta, ou fechados em uma extremidade, como é o caso dos tubos de um órgão. O comprimento de onda das ondas sonoras que são produzidas por esses dois tipos de tubos é bastante diferente.

No caso de tubos abertos nas duas extremidades, a freqüência fundamental corresponde a um comprimento de onda que é o dobro do comprimento L do tubo, ou seja,

l₁= 2L

Os harmônicos sucessivos têm comprimentos de onda na mesma razão que os de uma corda vibrante, ou seja,

l_n=2L/n

tomando n os valores sucessivos 1, 2, 3, ...

As freqüências correspondentes são dadas por f_n= v/l_n, ou seja,

f_n= nv/2L

onde v é a velocidade de propagação do ar contido no tubo.

Podemos admitir, em primeira aproximação, que v = 340 m/s, que corresponde à velocidade no ar seco a 15^o C e pressão normal. Se diminuirmos a pressão, a velocidade de propagação diminui, de modo que, por exemplo, uma flauta produz freqüências menores (sons mais graves) no topo de uma montanha do que ao nível do mar.

No caso de tubos fechados em uma extremidade, a freqüência fundamental corresponde a um comprimento de onda que é quatro vezes o comprimento L do tubo, ou seja,

l₁= 4L

Os harmônicos sucessivos têm comprimentos de onda decrescentes na mesma razão que os de uma corda vibrante, ou seja,

l_n=4L/n

tomando n os valores sucessivos 1, 2, 3, ...

As freqüências correspondentes são dadas por f_n= v/l_n, ou seja,

f_n= nv/4L

onde v é a velocidade de propagação do ar contido no tubo.

Neste caso, também, podemos admitir, em primeira aproximação, que v = 340 m/s, que corresponde à velocidade no ar seco a 15^o C e pressão normal. Se diminuirmos a pressão, a velocidade de propagação diminui, de modo que, por exemplo, um órgão produz freqüências menores (sons mais graves) no topo de uma montanha do que ao nível do mar.

EXEMPLO: Deseja-se construir um órgão que emita as seguintes freqüências (Hz):

dó3 f=261,000

ré3 f=293,625

mi3 f=326,250

fá3 f=348,000

sol3 f=391,500

lá3 f=435,000

si3 f=489,375

Calcular o comprimento de cada tubo de ar, fechado em uma extremidade, considerando a velocidade de propagação igual a 340m/s.

Para o harmônico fundamental vale a relação

L=v/4f

de modo que, introduzindo os valores das sete notas musicais acima fornecidos (Base do Diapason Normal), obtemos os comprimentos dos sete tubos:

dó3 L=0,32567 m

ré3 L=0,28948 m

mi3 L=0,26054 m

fá3 L=0,24425 m

sol3 L=0,21711 m

lá3 L=0,19540 m

si3 L=0,17369 m

Fica evidente que:

a) um tubo de maior comprimento emite um som fundamental de menor freqüência (mais grave)

b) a relação entre os comprimentos dos tubos é o inverso da relação entre as freqüências das notas musicais.Por exemplo, o comprimento do tubo da nota ré é igual a 8/9 do comprimento do tubo da nota dó, isto é, no caso deste exemplo, 0,28948=0,32567x(8/9). Existe uma diferença após a quinta casa decimal em virtude da aproximação feita no cálculo das freqüências.

c) se desejarmos emitir sons de freqüências n vezes maiores daquelas constantes dos valores acima, devemos dividir por n o tamanho dos tubos.

d) se desejarmos emitir sons de freqüências n vezes menores daquelas constantes dos valores acima, devemos multiplicar por n o tamanho dos tubos.

e) na fabricação de um órgão comercial os valores obtidos não são reais pois, no caso, fórmulas mais elaboradas são utilizadas, além de valores empíricos que levam em conta fatores como o material do tubo, sua rugosidade interna, sua rigidez, seu diâmetro e outros fatores construtivos do órgão.

O exercício anterior pode perfeitamente ser desenvolvido em seu Laboratório Virtual. Além disso, você pode construir um conjunto de tubos de PVC de modo que assoprando de forma perpendicular à extremidade aberta do tubo você poderá obter as freqüências acima dadas com boa aproximação.

EXEMPLO: determinar o comprimento de um tubo fechado em uma extremidade que emite a 15^O C a nota si3.

Para essa nota a freqüência é 435x9/8=489,375 Hz. Logo, sendo o tubo fechado em uma extremidade, o seu comprimento é dado por L=v/4f=340/4x489,375=0,17369 m. Se o tubo fosse aberto nas duas extremidades (digamos uma flauta) esse comprimento dobraria e seria igual a 0,34738 m.

EXEMPLO: Qual a freqüência da nota fa2?

Sabemos que o la3 corresponde a 435 Hz. Logo o do3 tem uma freqüência de 435x(3/5)=261 Hz. Resulta que o do2 tem uma freqüência de 261/2=130,5 Hz. Logo, o fa2 tem uma freqüência de 130,5x(4/3)=174 Hz.

NOTA: as relações das freqüências das notas são dadas no parágrafo 3.1 deste resumo.

[ topo ]

8.3. MEMBRANAS VIBRANTES

A teoria de uma membrana vibrante foge totalmente ao nível deste resumo de Física pois envolve funções matemáticas complexas devidas ao matemático francês Charles Bessel. Entretanto, para uma membrana circular como a de um tambor, podemos fornecer as freqüências de vibração dos vários harmônicos em função do raio da membrana. Os modos possíveis de vibração correspondem à vibrações de ondas concêntricas de vários comprimentos e de ondas em forma de anéis semicirculares, conforme ilustrado na Figura 8.2.

FIGURA 8.2 - ALGUNS MODOS POSSÍVEIS DE VIBRAÇÃO DE UMA MEMBRANA CIRCULAR PRESA EM SUA BORDA. AS DIFERENTES CORES INDICAM LOMBADAS OU DEPRESSÕES DA MEMBRANA.

Na Figura 8.2 a primeira fileira corresponde aos três primeiros modos de vibração com simetria circular e a segunda fileira aos três primeiros modos de vibração transversal. As freqüências em Hz desses modos são fornecidas na tabela 8.1.

TABELA 8.1 - FATORES DE FREQÜÊNCIA DOS PRIMEIROS MODOS DE VIBRAÇÃO DE UMA MEMBRANA CIRCULAR DE RAIO R.

A Tabela 8.1 fornece valores pR em segundos. As freqüências correspondentes são obtidas dividindo esses fatores pelo raio R (em metros) da membrana, multiplicando pela velocidade v de propagação das vibrações na membrana (em m/s) e dividindo o resultado por 2p.

Ou seja, a freqüência em Hz de um modo de vibração de uma membrana de raio R é dada por

f=(pR)xv/(2pR)

A velocidade de propagação das vibrações transversais em uma membrana de densidade r (kg/m³) sujeita a uma tensão T (N/m²) é dada por

v=(T/r)^1/2

EXEMPLO: calcular a freqüência do modo fundamental de vibração de uma membrana de raio igual a 20cm e densidade igual a 1,5g/cm³, sujeita a uma tensão superficial de 1600 N/cm².

Nessa membrana a velocidade de propagação das ondas transversais é v= (1600x10000/1,5x1000)^1/2 = 103 m/s. Utilizando a fórmula da freqüência para o modo fundamental obtemos

f = pRxv/2pR = 2,405x103/6,28x0,2 = 197 Hz

Essa freqüência é inferior ao do₃ (f=261 Hz) e se encontra na escala 2. O do2 tem uma freqüência de 130,5 Hz (261/2). A relação 197/130,5 = 1,5 = 3/2. Assim, a nota emitida pela membrana é próxima do sol₂ (f=130,5x3/2=195,75 Hz).

[ topo ]

[ início | sumário | voltar | avançar ]