Mn se k>0, de maneira que não
ocorrem repetições. Estas seqüências, que formam um conjunto
não enumerável, podem concebivelmente se aproximar de
seqüências periódicas assintoticamente e ser
quase-periódicas, ou podem ser não periódicas.
Finalmente, considere duas seqüências Mo, M1,…
e M0', M1',… onde Mo'=Mo+
ε. Então para um k
dado, se ε
é suficientemente pequeno, Mk'=Mk
± 2k
ε. Todas as seqüências,
portanto, são instáveis em relação a pequenas modificações.
Em particular, todas as seqüências periódicas são instáveis,
e nenhuma outra seqüência pode se aproximar delas
assintoticamente. Todas as seqüências exceto um conjunto de
medida zero são, portanto, não periódicas, e correspondem a
trajetórias não periódicas.
Voltando à Fig. 4, vemos que podem ser encontradas seqüências
periódicas análogas às tabuladas acima. Elas estão dadas
aproximadamente por
398,…
377, 410, …
369, 391, 414, …
362, 380, 419, …
As trajetórias que possuem estas ou outras seqüências
periódicas de máximos são provavelmente periódicas ou
quase-periódicas em si.
As seqüências acima se aproximaram temporariamente na solução
numérica de seqüências que começam nas iterações 5340, 4881,
3625, e 3926. Como a solução numérica eventualmente parte de
cada uma dessas seqüências, cada uma é provavelmente
instável.
Em um amplo sentido, se Mn' = Mn+
ε, e se
ε é suficientemente
pequeno, Mn+k'=Mn+k+Λє,
onde Λ é o produto das inclinações da curva na Fig. 4
nos pontos cujas abscissas são Mn,... Mn+k-1.
Como a curva aparentemente tem uma inclinação cuja magnitude
excede a unidade em todos os pontos, todas as seqüências dos
máximos, e portanto todas as trajetórias, são instáveis. Em
particular, as trajetórias periódicas, cujas seqüências de
máximos formam um conjunto enumerável, são instáveis, e
somente trajetórias excepcionais, que têm as mesmas
seqüências de máximos, podem se aproximar delas
assintoticamente. As trajetórias restantes, cujas seqüências
de máximos formam um conjunto não enumerável, portanto,
representam o fluxo não periódico determinístico.
Estas conclusões foram baseadas em um segmento finito de uma
solução determinada numericamente. Não podem ser
consideradas como matematicamente provadas, embora a
evidência delas seja forte. Uma aparente contradição requer
análise adicional.
É difícil reconciliar a mistura de duas superfícies, cada uma
contendo uma espiral, com a incapacidade de se mesclar as
duas trajetórias. Não é difícil, contudo, explicar a
aparente mistura das superfícies. Em dois tempos
τ0 e
τ1, os volumes
ocupados por um conjunto específico de partículas satisfazem
a relação

de acordo com (30). Um ciclo típico ao redor de C ou
C' requer cerca de 70 repetições, de maneira que,
para esse circuito
|
τ2= τ1+0.7,
e, como σ+b+1=41/3,
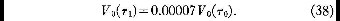
Duas partículas separadas entre si em uma direção adequada
podem, portanto, se reunir muito rapidamente, e parecer que
se misturam.
Veríamos, então, que as duas superfícies só parecem se misturar, e
continuam sendo superfícies diferentes. Seguindo estas
superfícies ao longo de um caminho paralelo a uma
trajetória, e circundando C ou C', vemos que
cada superfície é na verdade um par de superfícies, de
maneira que, onde elas parecem se misturar, na verdade há
quatro superfícies. Continuando este processo para outro
ciclo, vemos que na verdade há oito superfícies, etc., e
finalmente concluímos que há um infinito complexo de
superfícies, cada extremamente perto de uma ou uma outra de
duas superfícies que se misturam.
O infinito conjunto de valores no qual uma linha paralela ao eixo
X cruza estas superfícies pode ser comparado ao
conjunto de todos os números entre zero e um cujas expansões
decimais (ou algumas outras expansões além das binárias)
contêm somente zeros e uns. Este conjunto é simplesmente não
enumerável, em vista de sua correspondência com o conjunto
de todos os números entre zero e um, expressos em binário.
Não obstante forma um conjunto de medida zero. A seqüência
de uns e zeros correspondente a uma superfície em particular
contém uma história das trajetórias que ficam nessa
superfície, um um ou um zero imediatamente à direita do
ponto decimal indicando que o último circuito estava ao
redor de C ou C', respectivamente, um um ou um
zero no segundo lugar dando a mesma informação a respeito do
próximo ao último circuito, etc. Expansões decimais
repetidas representam trajetórias periódicas ou
quase-periódicas, e, como elas definem frações racionais,
formam um conjunto enumerável.
Se visualiza-se primeiro este complexo infinito de superfícies, não
seria difícil representar trajetórias determinísticas não
periódicas incluídas nestas superfícies.
8. Conclusão
Certos sistemas hidrodinâmicos não conservativos forçados
mecânica ou termicamente podem exibir comportamento tanto
periódico quanto irregular quando não há irregularidade ou
periodicidade obviamente relacionada no processo de
forçamento. Tanto o fluxo periódico quanto o não periódico
são observados em alguns modelos experimentais quando o
processo de forçamento é mantido constante, dentro dos
limites do controle experimental. Alguns sistemas finitos de
equações diferenciais ordinárias programadas para
representar estes sistemas hidrodinâmicos possuem soluções
analíticas periódicas quando o forçamento é estritamente
constante. Outros sistemas semelhantes produzem soluções
numéricas não periódicas.
Um sistema finito de equações diferenciais ordinárias que
representa o fluido dissipativo forçado freqüentemente tem a
propriedade que todas estas soluções são finalmente
confinadas dentro dos mesmos limites. Temos estudado em
detalhe as propriedades de soluções de sistemas deste tipo.
Nossos principais resultados se relacionam à instabilidade
das soluções não periódicas. Uma solução não periódica sem
componentes transitórios |