M_n if k>0, so that no repetitions occur. These sequences, which form a nondenumerable set, may conceivably approach periodic sequences asymptotically and be quasi-periodic, or they may be nonperiodic.
Finally, consider two sequences M_o, M₁,… and M₀', M₁',… " where Mo'=Mo+ε. Then for a given k, if ε is sufficiently small, M_k'=M_k  ± 2^kε. All sequences are therefore unstable with respect to small modifications. In particular, all periodic sequences are unstable, and no other sequences can approach them asymptotically. All sequences except a set of measure zero are therefore nonperiodic, and correspond to nonperiodic trajectories.
Returning to Fig, 4, we see that periodic sequences analogous to those tabulated above can be found. They are given approximately by

398,…
377, 410, …
369, 391, 414, …
362, 380, 419, … 

The trajectories possessing these or other periodic sequences of maxima are presumably periodic or quasi-periodic themselves.
The above sequences are temporarily approached in the numerical solution by sequences beginning at iterations 5340, 4881, 3625, and 3926. Since the numerical solution eventually departs from each of these sequences, each is presumably unstable.
More generally, if M_n' = M_n+ε, and if E is sufficiently small, M_n+k'=M_n+k+Λε, where Λ is the product of the slopes of the curve in Fig. 4 at the points whose abscissas are M_n,... M_n+k-1. Since the curve apparently has a slope whose magnitude exceeds unity everywhere, all sequences of maxima, and hence all trajectories, are unstable. In particular, the periodic trajectories, whose sequences of maxima form a denumerable set, are unstable, and only exceptional trajectories, having the same sequences of maxima, can approach them asymptotically. The remaining trajectories, whose sequences of maxima form a nondenumerable set, therefore represent deterministic nonperiodic flow.
These conclusions have been based upon a finite segment of a numerically determined solution. They cannot be regarded as mathematically proven, even though the evidence for them is strong. One apparent contradiction requires further examination.
It is difficult to reconcile the merging of two surfaces, one containing each spiral, with the inability of two trajectories to merge. It is not difficult, however, to explain the apparent merging of the surfaces. At two times τ₀ and τ₁, the volumes occupied by a specified set of particles satisfy the relation 

according to (30). A typical circuit about C or C' requires about 70 iterations, so that, for such a circuit,

 

τ₂= τ₁+0.7, and, since σ+b+1=41/3,                     

 

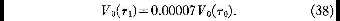
Two particles separated from each other in a suitable direction can therefore come together very rapidly, and appear to merge.
It would seem, then, that the two surfaces merely appear to merge, and remain distinct surfaces. Following these surfaces along a path parallel to a trajectory, and circling C or C', we see that each surface is really a pair of surfaces, so that, where they appear to merge, there are really four surfaces. Continuing this process for another circuit, we see that there are really eight surfaces, etc., and we finally conclude that there is an infinite complex of surfaces, each extremely close to one or the other of two merging surfaces.
The infinite set of values at which a line parallel to the X-axis intersects these surfaces may be likened to the set of all numbers between zero and one whose decimal expansions (or some other expansions besides binary) contain only zeros and ones. This set is plainly nondenumerable, in view of its correspondence to the set of all numbers between zero and one, expressed in binary. Nevertheless it forms a set of measure zero. The sequence of ones and zeros corresponding to a particular surface contains a history of the trajectories lying in that surface, a one or zero immediately to the right of the decimal point indicating that the last circuit was about C or C', respectively, a one or zero in second place giving the same information about the next to the last circuit, etc. Repeating decimal expansions represent periodic or quasi-periodic trajectories, and, since they define rational fractions, they form a denumerable set.
If one first visualizes this infinite complex of surfaces, it should not be difficult to picture nonperiodic deterministic trajectories embedded in these surfaces. 

8. Conclusion

Certain mechanically or thermally forced nonconservative hydrodynamical systems may exhibit either periodic or irregular behavior when there is no obviously related periodicity or irregularity in the forcing process. Both periodic and nonperiodic flow are observed in some experimental models when the forcing process is held constant, within the limits of experimental control. Some finite systems of ordinary differential equations designed to represent these hydrodynamical systems possess periodic analytic solutions when the forcing is strictly constant. Other such systems have yielded nonperiodic numerical solutions.
A finite system of ordinary differential equations representing forced dissipative flow often has the property that all of its solutions are ultimately confined within the same bounds. We have studied in detail the properties of solutions of systems of this sort. Our principal results concern the instability of nonperiodic solutions. A nonperiodic solution with no transient component