As trajetórias periódicas são casos especiais de trajetórias quase-periódicas.
   Uma trajetória que não é quase-periódica será chamada de não periódica. Se P(t) é não periódica, P(t₁+τ) pode estar arbitrariamente próxima do P(t₁) para algum tempo t₁ e algum intervalo τ de tempo arbitrariamente largo, mas, se isso é assim, P(t+τ)  não pode permanecer arbitrariamente próximo ao P(t) à medida que t → ∞. Trajetórias não periódicas são certamente representações do fluxo não periódico determinístico, e são o principal assunto deste artigo.
   Trajetórias periódicas são obviamente centrais. Trajetórias centrais quase-periódicas incluem trajetórias periódicas múltiplas com períodos incomensuráveis, enquanto trajetórias não centrais quase-periódicas incluem as que se aproximam de trajetórias periódicas assintoticamente. Trajetórias não periódicas podem ser centrais ou não centrais.
   Agora podemos estabelecer o teorema de que uma trajetória com uma trajetória limite estável é quase-periódica. Pois se P₀(t) é uma trajetória limite de P(t), dois pontos diferentes P(t₁) e P(t₁+τ), com τ arbitrariamente largo, podem ser encontrados arbitrariamente perto de qualquer ponto P₀(t₀). Como P₀(t)  é estável, P(t) e P(t+τ) devem permanecer arbitrariamente perto de P₀(t+t₀-t₁), e portanto um do outro, à medida que t → ∞, e P(t) é quase-periódico.
   Segue imediatamente que uma trajetória central estável é quase-periódica, ou, equivalentemente, que uma trajetória central não periódica é instável.
   O resultado tem conseqüências de longo alcance quando o sistema em consideração é um sistema não periódico observável cujo estado futuro nós podemos decidir predizer. Isto implica que dois estados que diferem por quantidades imperceptíveis podem eventualmente evoluir em dois estados consideravelmente diferentes. Se, então, há um erro qualquer ao observar o estado presente – e em qualquer sistema real esses erros parecem inevitáveis – uma previsão aceitável de um estado instantâneo no futuro distante bem pode ser impossível.
   Quanto às trajetórias não centrais, segue que uma trajetória não central uniformemente estável é quase-periódica, ou, equivalentemente, uma trajetória não central não periódica não é uniformemente estável. A possibilidade de uma trajetória não central não periódica que seja estável mas não uniformemente estável ainda existe. Para o autor, pelo menos, essas trajetórias, embora possíveis no papel, não parecem características dos fenômenos hidrodinâmicos reais. Qualquer argumento de que o fluxo atmosférico, por exemplo, é representado por uma trajetória deste tipo levaria à improvável conclusão de que devemos dominar o prognóstico de longo alcance o mais rápido possível, porque, quanto mais esperamos mais difícil se tornará nossa tarefa.
   Resumindo, mostramos que, sujeito às condições de singularidade, continuidade e limitação prescritas no começo desta seção, uma trajetória central, que em certo sentido está livre de propriedades transitórias, é instável se ela é não periódica. Uma trajetória não central, que é caracterizada por propriedades transitórias, não é uniformemente estável se ela for não periódica, e,

se ela é completamente estável, sua verdadeira estabilidade é uma de suas propriedades transitórias, o que tende a desaparecer conforme o tempo avança. Em vista da impossibilidade de medir as condições iniciais precisamente, e através disso distinguir entre uma trajetória central e uma trajetória não central vizinha, todas as trajetórias não periódicas são efetivamente instáveis do ponto de vista da previsão prática. 

4. Integração numérica de sistemas não conservativos 

Os teoremas da última seção podem ser importantes somente se as soluções não periódicas das equações do tipo considerado realmente existirem. Como as funções do tempo estatisticamente estacionárias não periódicas não são facilmente descritas analiticamente, soluções não periódicas específicas provavelmente seriam encontradas mais rapidamente por procedimentos numéricos. Nesta seção examinaremos um procedimento de integração numérica que é especialmente aplicável aos sistemas de equações da forma (4). Numa seção posterior usaremos este procedimento para determinar uma solução não periódica de um conjunto simples de equações.
   Para resolver (1) numericamente podemos escolher um tempo inicial t₀ e um incremento de tempo Δt, e deixar

Então nós introduzimos as aproximações auxiliares

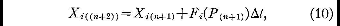
onde P_n e P_(n+1) são os pontos cujas coordenadas são

(X_1,n ,..., X_M,n) e (X_1(n+1),...,X_M(n+1))

O procedimento numérico mais simples para obter soluções aproximadas de (1) é o procedimento da diferença de avanço,

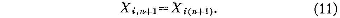
Em muitos casos melhores aproximações às soluções de (1) podem ser obtidas por um procedimento de diferença-centralizada.

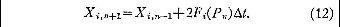
 Este procedimento é inadequado, porém, quando a natureza determinística de (1) é matéria de preocupação, já que os valores de X_1,n ,…, X_M,n  não determinam unicamente os valores de X_1,n+1, ..., X_M,.n+1.
   Um procedimento que amplamente supera as desvantagens dos procedimentos de diferença de avanço e de diferença centralizada é o procedimento da dupla aproximação, definido pela relação

Aqui o coeficiente de Δt, é uma aproximação ao tempo derivado de Xi  no tempo t₀+(n+1/2)Δt. De (9) e (10), segue que (13) pode ser re-escrito