|
< ε. Periodic trajectories are special
cases of quasi-periodic trajectories.
A trajectory which is not quasi-periodic
will be called nonperiodic. If P(t) is nonperiodic,
P(t1+τ) may be arbitrarily close to
P(t1) for some time t1 and
some arbitrarily large time interval τ, but,
if this is so, P(t+τ) cannot remain arbitrarily
close to P(t) as t → ∞. Nonperiodic
trajectories are of course representations of deterministic
nonperiodic flow, and form the principal subject of this paper.
Periodic trajectories are obviously central.
Quasi-periodic central trajectories include multiple periodic
trajectories with incommensurable periods, while quasi-periodic
noncentral trajectories include those which approach periodic
trajectories asymptotically. Nonperiodic trajectories may
be central or noncentral.
We can now establish the theorem that a trajectory with a
stable limiting trajectory is quasi-periodic. For if P0(t)
is a limiting trajectory of P(t), two distinct
points P(t1) and P(t1+τ),
with τ arbitrarily large, may be found arbitrary
dose to any point P0(t0). Since
P0(t) is stable, P(t) and P(t+τ)
must remain arbitrarily close to P0(t+t0-t1),
and hence to each other, as t → ∞,
and P(t) is quasi-periodic.
It follows immediately that a stable central
trajectory is quasi-periodic, or, equivalently, that a nonperiodic
central trajectory is unstable.
The result has far-reaching consequences
when the system being considered is an observable nonperiodic
system whose future state we may desire to predict. It implies
that two states differing by imperceptible amounts mar eventually
evolve into two considerably different states. If, then, there
is any error whatever in observing the present state-and in
any real system such errors seem inevitable-an acceptable
prediction of an instantaneous state in the distant future
may well be impossible.
As for noncentral trajectories, it follows
that a uniformly stable noncentral trajectory is quasi-periodic,
or, equivalently, a nonperiodic noncentral trajectory is not
uniformly stable. The possibility of a nonperiodic noncentral
trajectory which is stable but not uniformly stable still
exists. To the writer, at least, such trajectories, although
possible on paper, do not seem characteristic of real hydrodynamical
phenomena. Any claim that atmospheric flow, for example, is
represented by a trajectory of this sort would lead to the
improbable conclusion that we ought to master long-range forecasting
as soon as possible, because, the longer we wait, the more
difficult our task will become.
In summary, we have shown that, subject
to the conditions of uniqueness, continuity, and boundedness
prescribed at the beginning of this section, a central trajectory,
which in a certain sense is free of transient properties,
is unstable if it is nonperiodic. A noncentral trajectory,
which is characterized by transient properties, is not uniformly
stable it it is nonperiodic, and, |
if it is stable at all, its very stability
is one of its transient properties, which tends to die
out as time progresses. In view of the impossibility of measuring
initial conditions precisely, and thereby distinguishing between
a central trajectory and a nearby noncentral trajectory,
all nonperiodic trajectories are effectively unstable from
the point of view of practical prediction.
4. Numerical integration of nonconservative system
The theorems of the last section can be
of importance only if nonperiodic solutions of equations of
the type considered actually exist. Since statistically stationary
nonperiodic functions of time are not easily described analytically,
particular nonperiodic solutions can probably be found most
readily by numerical procedures. In this section we shall
examine a numerical-integration procedure which is
especially applicable to systems of equations of the
form (4). In a later section we shall use this procedure
to determine a nonperiodic solution of a
simple set of equations.
To solve (1) numerically we may choose an
initial time t0 and a time increment
Δt, and let

We then introduce the auxiliary approximations

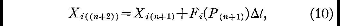
where Pn and P(n+1)
are the points whose coordinates are (X1,n
,..., XM,n) and (X1(n+1),...,XM(n+1)).
The simplest numerical procedure for obtaining approximate
solutions of (1) is the forward-difference procedure,
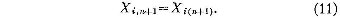
In many instances better approximations
to the solutions of (1) may be obtained by a centered-difference
procedure
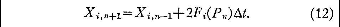
This procedure is unsuitable, however, when
the deterministic nature of (1) is a matter of concern, since
the values of X1,n ,…, XM,n
do not uniquely determine the values of X1,n+1,
..., XM.n+1.
A procedure which largely overcomes the disadvantages of
both the forward-difference and centered-difference procedures
is the double-approximation procedure, defined by the relation

Here the coefficient of Δt, is an approximation
to the time derivative of Xi at time t0+(n+1/2)Δt.
From (9) and (10), it follows that (13) may be rewritten

|