equations again, although a far simpler
set than the one which governs individual molecular motions.
In any real hydrodynamical system, viscous
dissipation is always occurring, unless the system is moving
as a solid, and thermal dissipation is always occurring,
unless the system is at constant temperature. For certain
purposes many systems may be treated as conservative systems,
in which the total energy, or some other quantity, does
not vary with time. In seeking the ultimate behavior of
a system, the use of conservative equations is unsatisfactory,
since the ultimate value of any conservative quantity would
then have to equal the arbitrarily chosen initial value.
This difficulty may be obviated by including the dissipative
processes, thereby making the equations nonconservative,
and also including external mechanical or thermal forcing,
thus preventing the system from ultimately reaching a state
of rest. If the system is to be deterministic, the forcing
functions, if not constant with time, must themselves vary
according to some deterministic role.
In this work, then, we shall deal specifically
with finite systems of deterministic ordinary differential
equations, designed to represent forced dissipative hydrodynamical
systems. We shall study the properties of nonperiodic solutions
of these equations.
It is not obvious that such solutions
can exist at all. Indeed, in dissipative systems governed
by finite sets of linear equations, a constant forcing leads
ultimately to a constant response, while a periodic forcing
leads to a periodic response. Hence, nonperiodic flow has
sometimes been regarded as the result of nonperiodic or
random forcing.
The reasoning leading to these conclusions
is not applicable when the governing equations are nonlinear.
If the equations contain terms representing advection -
the transport of some property of a fluid by the motion
of the fluid itself-a constant forcing can lead to a variable
response. In the rotating-basin experiments already mentioned,
both periodic and nonperiodic flow result from thermal forcing
which, within the limits of experimental control, is constant.
Exact periodic solutions of simplified systems of equations,
representing dissipative flow with constant thermal forcing,
have been obtained analytically by the writer (1962a). The
writer (1962b) has also found nonperiodic solutions of similar
systems of equations by numerical means.
2. Phase space
Consider a system whose state
may be described by M variables X1... XM. Let the system be
governed by the set of equations
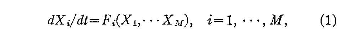
where time t is the single independent variable, and the functions
Fi possess continuous first partial derivatives. Such a system
may be studied by means of phase space –
|
an M-dimensional Euclidean space Γ
hose coordinates are X1, … , XM
. Each point in phase space represents a possible
instantaneous state of the system. A state which is varying
in accordance with (1) is represented by a moving particle
in phase space, traveling along a trajectory in
phase space. For completeness, the position of a stationary
particle, representing a steady state, is included as a trajectory.
Phase space has been a useful concept in
treating finite systems, and has been used by such mathematicians
as Gibbs (1902) in his development of statistical mechanics,
Poincaré (1881) in his treatment of the solutions of differential
equations, and Birkhoff (1927) in his treatise on dynamical
systems. From the theory of differential equations (e, g.,
Ford 1933, ch. 6), it follows, since the partial derivatives
∂Fi/∂X1 are
continuous, that if t0 is any time, and
if X10, …,XM0 is any point
in Γ, equations (1) possess a unique solution
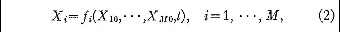
valid throughout some time interval containing t0
, and satisfying the condition
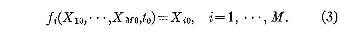
The functions fi are continuous in X10,…,
XM0 and t. Hence there is a unique trajectory
through each point of Γ. Two or more trajectories
mar, however, approach the same point or the same curve asymptotically
as t→ ∞ or as t→ -∞.
Moreover, since the functions fi are
continuous, the passage of time defines a continuous deformation
of any region of r into another region.
In the familiar case of a conservative system,
where some positive definite quantity Q, which mar
represent some form of energy, is invariant with time, each
trajectory is confined to one or another of the surfaces
of constant Q. These surfaces mar take the form of
closed concentric shells.
If, on the other hand, there is dissipation
and forcing, and if, whenever Q equals or exceeds some
fixed value Q1, the dissipation acts to
diminish Q more rapidly then the forcing can increase
Q, then (-dQ/dt) has a positive lower bound
where Q ≥ Ql, and each trajectory must ultimately
become trapped in the region where Q < Ql. Trajectories
representing forced dissipative flow mar therefore differ
considerably from those representing conservative flow. Forced
dissipative systems of this sort are typified by the system
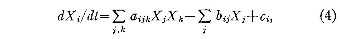
where ∑aijkXiXjXk
vanishes identically, ∑bijkXiXj
is positive definite, and c1,…, cM
are constants. If
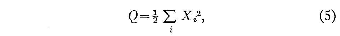
|