III - FRACTAIS
Ildeu de Castro Moreira
Universidade Federal do Rio de Janeiro.
O concreto é a parcela do abstrato que o uso tornou familiar.
Paul Langevin
Qual a geometria da natureza? Essa pergunta não parece ter uma resposta unívoca e precisa. Como Poincaré já chamava a atenção no início deste século, ao discutir o uso da geometria euclidiana ou de outras geometrias na descrição da estrutura do espaço-tempo, a resposta a ela não é absoluta. Não existe uma geometria intrínseca à natureza. Na tentativa de entender o seu entorno, o homem constrói e utiliza conceitos geométricos, escolhendo a geometria em função de sua comodidade e da maior adequação à descrição dos fenômenos. A chamada geometria fractal, da qual falaremos aqui e que trata dos conjuntos ou estruturas fractais, embora esteja em uma fase ainda incipiente, já ganhou, de alguns anos para cá, foros de um domínio científico reconhecido. Ela tem se mostrado uma interessante fonte de inspiração teórica e já encontrou aplicações variadas em muitas áreas das ciências físicas e matemáticas.
Com Galileu, no início do processo de matematização das 'leis da natureza' , que veio a se transformar em uma das características fundamentais da ciência moderna, vemos que são definidos, de início, os entes matemáticos apropriados para essa descrição. Para ele, embora a matemática seja "a língua na qual a natureza está escrita", não se trata de utilizar qualquer matemática, mas aquela que se expressa na linguagem das figuras geométricas descritas por ou compostas de retas e curvas (suaves, diríamos):
A filosofia está escrita nesse enorme livro que temos aberto diante dos olhos, o Universo. Mas não se pode entendê-lo antes de se aprender a entender a língua, de se conhecer os caracteres em que está escrito. Está escrito em língua matemática e seus caracteres são triângulos, círculos e outras figuras geométricas, sem as quais é impossível entender uma palavra sequer (...).
Esse trecho de Il saggiatore (O ensaiador), escrito em 1623, é muito conhecido e citado. Abre, inclusive, o primeiro capítulo de A geometria fractal da natureza (1975), de Benoit Mandelbrot[1(a)], considerado o livro que consolidou as bases da geometria fractal. No entanto, uma outra passagem muito instrutiva de O ensaiador é raramente mencionada. Nela, Galileu precisará ainda mais o que entende pelos caracteres da língua necessária e útil para descrever a natureza e eliminará claramente a possibilidade de serem utilizadas 'linhas irregulares':
Chamamos linhas regulares aquelas que (...) se podem definir e demonstrar delas seus acidentes e propriedades. Assim, a espiral é regular e se define dizendo que nasce de dois movimentos uniformes, um reto e outro circular; assim, a elipse que nasce de secção do cone e do cilindro. Porém, as linhas irregulares são aquelas que, não tendo determinação alguma, são infinitas e (...) indefiníveis. Não se pode demonstrar delas propriedade alguma, nem definitivamente saber nada sobre elas. Dizer-se: "Tal acidente ocorre graças a uma linha irregular", é o mesmo que dizer: "Não sei por que ocorre". A introdução de tal linha não é melhor que a introdução das simpatias, antipatias, propriedades ocultas, influências e outros termos usados por alguns filósofos como máscara da verdadeira resposta que é "não sei".
Newton, no início do Prefácio à primeira edição de seus Princípios matemáticos da filosofia natural (1686), uma das obras mais importantes de toda a história da ciência, faz considerações parecidas sobre as curvas nas quais a geometria se baseia:
(...) a descrição de linhas retas e círculos, sobre as quais a geometria se funda, pertence à mecânica. (...) é a glória da geometria que de poucos princípios, tirados do nada, ela é capaz de produzir tantas coisas.
Saltando mais de dois séculos, vamos reler trechos do grande experimentador francês Jean Perrin, em seu livro Les atomes, de 1913, no qual discute as evidências que levaram à comprovação da existência dos átomos e moléculas. Perrin analisa, em particular, seu trabalho experimental com o chamado movimento browniano, sobre o qual realizou uma série de experiências minuciosas, inspiradas em um trabalho teórico decisivo escrito por Einstein em 1905.
Perrin estava estudando o movimento de uma partícula muito pequena (um grão de pólen, por exemplo) dentro da água, quando observado em um microscópio. A trajetória que a partícula segue é extremamente irregular, no sentido de que muda de rumo a cada instante; essa mudança é ocasionada pelos choques com as moléculas do fluido que possuem um movimento de agitação térmica (Figura 24).
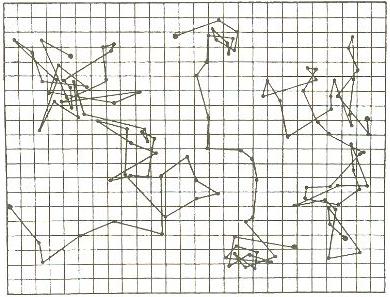 |
FIGURA 24 - Trajetória irregular do movimento browniano de
uma pequena partícula |
Perrin vai procurar convencer o leitor de que estas 'curvas irregulares' - que não têm uma estrutura suave e para as quais não se pode definir derivadas ao longo delas - podem ser utilizadas para modelar várias situações que surgem na natureza e que, até então, não tinham sido consideradas dignas de observação e análise. Diz Perrin:
Aqueles que ouvem falar de curvas [irregulares] sem tangentes, ou de funções sem derivadas, pensam freqüentemente que a natureza não apresenta tais complicações, e nem mesmo as sugere. O contrário, contudo, é verdadeiro, e a lógica dos matemáticos manteve-os mais próximos da realidade do que as representações empregadas pelos físicos (...).
Quando Perrin fala dos matemáticos e de sua lógica, está se referindo aos trabalhos de Riemann, Weierstrass, Cantor e outros que, na segunda metade do século XIX, introduziram e analisaram alguns monstros matemáticos, como funções que não tinham derivada em nenhum ponto ou conjuntos particularmente estranhos e complicados. Com certa perspectiva premonitória, Perrin, depois de dar como exemplo de fenômeno natural irregular o crescimento multiforme e dendrítico de um floco de neve, acrescenta:
Poderíamos encontrar situações nas quais o uso de uma função sem derivada fosse mais simples do que o de uma função que pudesse ser diferencíável. Quando isto ocorrer, o estudo matemático dos contínuos irregulares provará seu valor prático... Contudo, essa esperança é nada mais que um sonho, ainda.
Uma frase de Mandelbrot, escrita logo no primeiro parágrafo do seu livro, ficou famosa por conter uma espécie de slogan da nova geometria que se propunha: "Nuvens não são esferas, montanhas não são cones, linhas costeiras não são círculos, cascas de árvores não são suaves nem o raio se propaga em linha reta". A contraposição proposital às colocações de Galileu fica clara. Para se introduzir idéias científicas novas e revolucionárias, o aspecto de convencimento dos leitores, propagandístico diríamos, é também importante. Isso pode ser visto, por exemplo, em várias afirmações de Galileu e nos escritos de Mandelbrot. Nessas ocasiões são feitas afirmações peremptórias, que posteriormente podem vir a ser consideradas como exageradas, mas que fazem parte do jogo da ciência, uma atividade humana e socialmente condicionada.
Nos modelos matemáticos construídos, ao longo dos últimos séculos, para a descrição de fenômenos físicos e no uso tecnológico, especialmente nas máquinas, predominaram sempre as formas regulares: .a reta, o círculo (roda), a esfera, o cilindro, o triângulo, a elipse, a parábola e outras curvas similares. As funções diferenciáveis (redutíveis à reta na vizinhança do ponto) passaram a ser o ponto básico de partida para qualquer modelo dinâmico na física e na matemática aplicadas. Sua utilidade é inquestionável; mas seriam realmente as formas mais adequadas para melhor descrever todas as inúmeras formas naturais, inclusive as mais irregulares e multifacetadas? Com essa pergunta e essa visão, externada por Perrin e Mandelbrot, entre outros (ver o Apêndice para um sumário dos trabalhos pioneiros sobre estruturas fractais), a idéia dos fractais começa a surgir...
Neste texto discutiremos, de forma introdutória e não isenta de simplificações e omissões, os conceitos de fractal e de dimensão fractal e mencionaremos algumas das aplicações que essas idéias têm encontrado em diversos ramos do conhecimento. O leitor interessado em se aprofundar no assunto poderá consultar alguns dos livros listados nas referências (1 a 10).
O QUE SÃO FRACTAIS?
Os fractais são conjuntos cuja forma é extremamente irregular ou fragmentada: e que têm essencialmente a mesma estrutura em todas as escalas. A origem do termo fractal, introduzido por Mandelbrot, está no radical fractus, proveniente do verbo latino frangere, que quer dizer quebrar, produzir pedaços irregulares; vem da mesma raiz a palavra fragmentar, em português.
As principais propriedades que caracterizam e que permitem definir os conjuntos fractais são as seguintes: 1) a auto-similaridade, que pode ser exata ou estatística, ou seja, o sistema é invariante (mantém a mesma forma e estrutura) sob uma transformação de escala (transformação que reduz ou amplia o objeto ou parte dele); 2) a extrema 'irregularidade' no sentido de rugosidade (não-suavidade) ou fragmentação; 3) possuir, em geral, uma dimensão fractal não-inteira. A dimensão fractal, como veremos adiante, quantifica, de certo modo, o grau de irregularidade ou fragmentação do conjunto considerado.
Mas existem objetos ou estruturas naturais que são fractais? A resposta a essa pergunta nos remete novamente às considerações de Poincaré sobre qual é a geometria da natureza. Os fractais são conjuntos definidos por certas propriedades matemáticas e, portanto, têm legitimidade como um conceito matemático coerentemente definido e correlacionado com outros. Se serão úteis em aplicações práticas, é uma outra questão. Mas o que se nota é que muitas estruturas ou processos naturais têm propriedades similares às dos fractais, em particular a simetria de escala, e que podem, portanto, ser descritos por eles, pelo menos em determinados domínios. Não custa lembrar também o ponto de vista otimista, expresso por, entre outros, Pascal e Dirac, para os quais os produtos da nossa imaginação (equações, por exemplo), quando dotados de beleza matemática, sempre encontrarão algum uso na modelagem física da natureza.
O QUE SÃO E COMO MEDIR AS DIMENSÕES FRACTAIS?
A noção de dimensão é uma questão fundamental tanto na matemática quanto na física. Vamos discuti-Ia de um modo superficial, mas que nos ajude a entender a idéia de dimensão fractal. Duas idéias próximas, mas diversas, estão ligadas ao termo dimensão usualmente empregado: 1) o número de informações (no caso, dadas pelas coordenadas) necessárias para se localizar um ponto no espaço: falamos que o espaço possui três dimensões. Após a teoria da relatividade, a idéia de um espaço quadridimensional se firmou na física, com a introdução também da dimensão temporal para a caracterização de um evento que ocorre no espaço-tempo; 2) a noção de medida de comprimento. Assim, dizemos, por exemplo, que a dimensão de um objeto é 50cm.
Uma noção importante de dimensão, a chamada dimensão topológica, relacionada à primeira idéia, foi discutida por Poincaré em 1911 e por Brouwer, em 1913. Diz o seguinte: um contínuo tem n dimensões quando podemos dividi-lo por meio de cortes que sejam eles próprios contínuos de (n-1) dimensões. Considera-se que o ponto possui dimensão zero. Por essa definição, a reta terá dimensão 1 (porque pode ser separada por um ponto), o plano terá dimensão 2 (porque pode ser separado por uma reta), o espaço usual terá três dimensões (porque pode ser separado por um plano: as paredes de uma casa, por exemplo), e assim, sucessivamente, podemos imaginar conjuntos contínuos com um número crescente de dimensões. Note-se que, nessa definição, não entra a noção de medida de distância (métrica), que, como dissemos, aparece também associada ao termo dimensão. Trata-se aqui de uma noção topológica, relacionada apenas à noção de vizinhança (proximidade) entre os pontos de um conjunto, o que permite a definição de continuidade.
Vamos considerar agora o aspecto métrico ligado à noção de dimensão. Neste século surgiram várias noções de dimensão, às vezes não-equivalentes, baseadas nessa característica. A primeira delas é a denominada capacidade, definida por Kolmogorov, que mede o quanto o conjunto ou objeto considerado preenche o espaço em que está imerso. Por ser, talvez, a definição de dimensão mais simples que permite caracterizar os fractais, é usualmente chamada de dimensão fractal, embora existam, como veremos, vários outros tipos de dimensões métricas utilizadas para caracterizar os graus de 'fractalidade' de um conjunto. Essa definição de capacidade é bastante próxima da noção de dimensão introduzida por Hausdorff, em 1919.
A definição da capacidade dcap de um conjunto é a seguinte:
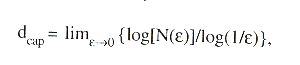 |
(1) |
1. Conjunto de Cantor. É um conjunto construído da seguinte maneira: tomamos um segmento de reta e o partimos em três segmentos iguais. Em seguida, o pedaço intermediário é retirado. Os dois segmentos restantes são de novO repartidos em três segmentos iguais e os segmentos intermediários são retirados. O processo de repartir os segmentos e de retirar o pedaço intermediário prossegue ad infinitum. O Conjunto de Cantor é o conjunto de pontos restantes, após infinitas operações terem sido realizadas.
A capacidade, ou dimensão fractal, desse conjunto, como pode ser inferido diretamente da Figura 25, vale: dcap = log(2)/log(3) ≈ 0,6. Isto porque, em cada etapa do processo de construção do conjunto, utilizamos dois segmentos (cubos elementares) para cobrir a figura, sendo que cada segmento elementar tinha comprimento de 113. Observe-se que esse conjunto tem comprimento zero, porque, a cada etapa do processo, seu comprimento é reduzido por um fator 2/3. Logo, seu comprimento, no limite em que n → ∞, será L = (2/3)n → 0.
 |
| FIGURA 25 - Processo de formação do Conjunto de Cantor |
2. Conjunto de Koch: Este conjunto é construído como indicado na Figura 26. Em vez de retirarmos o pedaço intermediário do segmento inicial, nós o substituímos por mais dois segmentos iguais, como indicado. Percebe-se logo que a dimensão fractal desse conjunto será dada por dcap= log(4)/log(3) ≈ 1,26. O comprimento desse conjunto tende para infinito, valendo em cada etapa do processo de construção (4/3)n.
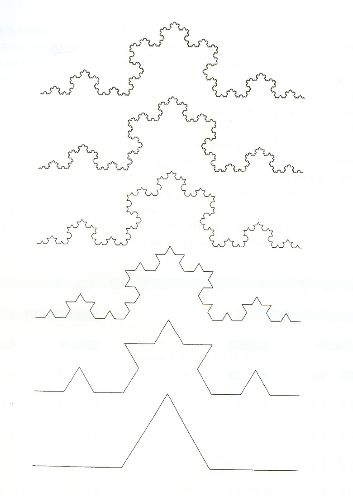 |
| FIGURA 26 - Processo de formação do Conjunto de Koch |
Muitos outros conjuntos fractais similares podem ser imaginados com regras de construção semelhantes. O leitor poderá facilmente se convencer, pelo uso da definição (1), que a dimensão fractal de uma reta é 1, a do plano vale 2 e a do espaço usual é 3, coincidentes com a dimensão topológica. A figura 27 exibe um fractal, chamado de esponja de Menger, que tem dimensão fractal maior que 2 (dcap ≈ 2,727).
 |
| FIGURA 27 - Esponja de Menger |
Uma característica estranha que surge logo à primeira vista, com esses fractais, é a presença de dimensões que não são números inteiros. Isso ocorre em aparente contradição com nossa 'intuição', que espera que os objetos tenham dimensão inteira n = 1, 2, 3, etc.; a dimensão topológica, por sua definição exposta acima, satisfaz essa propriedade 'intuitiva'. A dimensão (capacidade) dos conjuntos fractais é maior ou igual à sua dimensão topológica. Mas vamos procurar mostrar que a idéia de uma dimensão não-inteira não é absurda, que ela pode ser expressa matematicamente de forma coerente e que pode mesmo fornecer informações interessantes sobre o grau de 'fractalidade' e de ocupação, pela estrutura analisada, do espaço no qual está imersa. Note-se que poderão existir fractais cuja dimensão é inteira; isso ocorre, por exemplo, com a trajetória de uma partícula no movimento browniano, cuja capacidade é 2.
Tomemos um exemplo concreto bem simples, e que já se tomou clássico, para mostrar que a idéia de dimensão fracionária não é tão absurda como parece: a medida do comprimento da linha costeira de um país. Richardson chamou a atenção, em 1961, para o fato de que esse comprimento não é uma quantidade bem definida como em geral se imagina: seu valor depende do comprimento da 'régua' (unidade de medida) que é escolhida para medi-Ia. Assim, se tomamos unidades de medida cada vez menores (primeiro 10km, depois 1 km, em seguida 100m, e assim sucessivamente), o comprimento da linha costeira, em função de suas inúmeras reentrâncias, cresce proporcionalmente na medida em que E (comprimento da 'régua' utilizada) decresce; a relação, proveniente de (1), tem a forma: L(ε) ~ ε1-d, onde d é a dimensão fractal. Esse tipo de dependência de uma quantidade, no caso L, em relação a outra, ε neste caso, é chamada de lei de potência.
Você poderá tomar um mapa, da Baía de Guanabara, por exemplo, e verificar através da medida da periferia da baía, tomando várias 'réguas' como sua unidade básica de medida, que a dimensão fractal obtida, como ocorre com as linhas costeiras de outros países analisadas por Richardson, fica em tomo de 1,25; trata-se de um valor próximo da dimensão fractal da Curva de Koch, embora esta seja um fractal exato e não estatístico.
Um método de se medir a dimensão fractal de um conjunto: a contagem por caixa
Nos exemplos acima, como o processo de construção do conjunto é bastante simples e sempre igual em cada escala, fica fácil o cômputo da dimensão fractal. Para se medir a dimensão fractal de estruturas naturais ou de fractais aproximados ou estatísticos, devemos realizar uma análise mais cuidadosa. Note-se que, para objetos naturais, o processo de escalonamento tem limites e só funciona dentro de uma certa faixa de escalas. Em geral, se pode ir até uma certa escala inferior cujo valor é determinado pelo tamanho dos constituintes elementares do objeto (ou pela precisão das medidas), ou seja, chega-se a um ponto onde não se pode mais ampliar as partes do objeto e ainda se obter uma estrutura similar. O processo tem também um limite superior dado pelo tamanho finito do objeto considerado. Existem vários procedimentos de medição da dimensão fractal já propostos; vamos discutir um deles e aplicá-lo a um conjunto importante, no plano, que emana do estudo dos sistemas dinâmicos não-lineares.
O procedimento básico é o seguinte: divide-se a área (ou volume) do conjunto analisado em um certo número de caixas (cubos elementares) iguais. Conta-se o número de caixas em que existe pelo menos um ponto do conjunto. Reduz-se sucessivamente o tamanho das caixas e mede-se, a cada vez, o número de caixas que possuem pelo menos um ponto do conjunto. Desenha-se o gráfico do logaritmo de N (número de caixas ocupadas) em função do logaritmo de (1/ε), onde ε é a dimensão linear da caixa, em cada etapa. A dimensão fractal do conjunto é dada pelo valor da inclinação do gráfico.
Consideremos o chamado Atrator de Hénon, uma figura que surge quando aplicamos a seguinte transformação para obter pontos sucessivos no plano (X,Y):
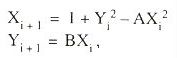 |
(2) |
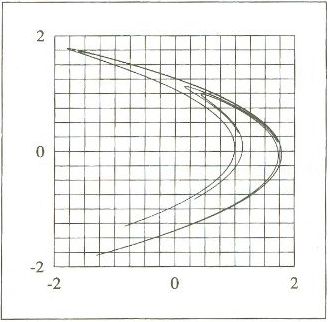 |
| FIGURA 28 - Atrator de Hénon e o cálculo de sua dimensão fractal |
Esse método de medida da dimensão fractal tem algumas limitações. Ele não distingue caixas com números diferentes de pontos e, portanto, não é muito adequado para descrever fractais probabilísticos ou aqueles resultantes de um processo dinâmico complicado, já que não permite determinar quais caixas são visitadas com maior freqüência. Além disso, de um ponto de vista operacional, o método converge lentamente e o número de caixas necessário para se efetuar a medida cresce rapidamente, tornando-se pouco prático para dimensões maiores que dois. Existem outros métodos alternativos de medida da dimensão fractal, mas não trataremos deles aqui. O leitor interessado poderá consultar os livros citados nas referências, nos quais alguns desses métodos são discutidos.
Outras definições de dimensões fractais
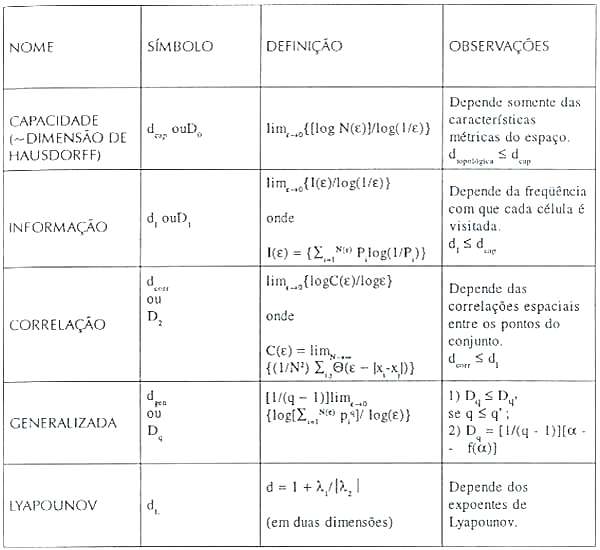
Da análise anterior, começa também a ficar claro que outras definições de dimensão fractal são possíveis. De alguns anos para cá, várias delas foram introduzidas, destacando aspectos variados da 'fractalidade' de um conjunto. O Quadro 1 apresenta um sumário das definições de dimensão mais utilizadas. Significativamente, em 1983, foi definida uma noção de dimensão fractal generalizada que incorpora muitas das definições anteriores em um esquema único e progressivo.
Dimensão de informação. É uma certa generalização da capacidade, que leva em conta a probabilidade relativa de ocupação dos cubos elementares usados para cobrir o conjunto. Fornece o mesmo valor que a capacidade se as probabilidades de visita a todos os cubos forem idênticas.
Dimensão de correlação. Quantifica o número de pontos que estão a uma distância menor que e de um dado ponto. A função de correlação C (ε,r) mede o número de pontos situados dentro de uma distância ε e a dimensão de correlação é uma média disso, tomada sobre cada par de pontos. As três definições anteriores de dimensão fractal podem ser vistas, como se observa no Quadro 1, como casos particulares de uma noção mais geral de dimensão fractal, denominada dimensão generalizada, que caracteriza o conjunto através de todo um espectro de dimensões. Com isso, estruturas fractais mais complexas podem ser analisadas. Os conjuntos para os quais as dimensões generalizadas Dq não fornecem resultados idênticos são denominados de multifractais. Eles descrevem situações em que diferentes regiões de um objeto têm diferentes propriedades fractais.
Dimensão de Lyapounov. Trata-se de uma noção de dimensão bem diversa das anteriores. Está ligada ao comportamento temporal dos sistemas dinâmicos. Parte-se, aqui, da idéia de que os expoentes de Lyapounov (que medem a taxa exponencial média de esticamento ou contração, em direções características, de trajetórias que geram a figura de um atrator no espaço de fase) estão relacionados à dimensão fractal do atrator. A definição dessa dimensão, em duas dimensões, é: d = 1 + λ1/|λ2|, onde os λi são os expoentes de Lyapounov. Essa dimensão, que pode ser calculada computacionalmente, é, em alguns casos, igual à dimensão fractal fornecida pelas outras definições.
| Quadro 1 - Definições de dimensão fractal |
 |
MÉTODOS DE GERAÇÃO DE FRACTAIS
Existem muitos métodos de geração de estruturas fractais através de modelos matemáticos simples. Vamos aqui dar destaque a dois deles, pela sua importância e caráter bastante genérico: a geração de fractais por agregação e o método IFS (Iterated Function System). Outro importante método de geração algorítmica de fractais provém dos autômatos celulares; não o consideraremos aqui, já que outro artigo deste livro é especialmente dedicado a eles.
Geração de fractais por agregação
Vários procedimentos, sugeridos pelos processos de agregação de materiais que são observados na natureza, têm sido imaginados dentro desta perspectiva de construção de fractais. Entre os processos naturais em que podem ocorrer fenômenos de agregação mencionam-se: a eletrodeposição, a junção de partículas de fumaça ou poeira, os aglomerados de galáxias e até a formação de colônias de bactérias. A idealização desses processos leva a modelos matemáticos simplificados, que são construídos computacionalmente, através de um algoritmo; apesar de sua simplicidade, eles podem conter elementos essenciais do processo natural que se pretende descrever e produzir estruturas bastante complexas. Vamos nos limitar a dois deles.
Modelo DLA (Diffusion-Limited Aggregation)
Neste modelo, introduzido por Witten e Sander em 1981[11], uma partícula, que dará início ao agregado, e é por isso chamada de semente, é colocada inicialmente no centro de uma rede (no computador, no centro da tela). A cada vez é introduzida na borda do domínio considerado (na borda da tela) uma nova partícula que se move em movimento aleatório. Quando a partícula encontra um sítio vizinho ocupado por outra partícula, fica grudada nele. Então, outra partícula é liberada nas bordas, numa posição inicial aleatória. Figuras complexas e similares a estruturas naturais provenientes de deposição de materiais, como a da Figura 29, emergem nesse processo.
 |
| FIGURA 29 - Figura construída pelo método DLA (Diffusion-Limited Aggregation) |
Na sua forma básica, esse modelo leva à produção de estruturas fractais com dimensão 1,71 no plano e 2,5 no espaço, aproximadamente. Entre suas aplicações podemos citar: a eletrodeposição (formação de depósito no catodo pela passagem de corrente elétrica), que leva a uma dimensão fractal aproximada de 2,43; o problema da ruptura dos dielétricos, quando submetidos a diferenças grandes de potencial, cuja dimensão fractal característica fica em torno de 1,7. A agregação de colóides e o crescimento de cristais são outros domínios onde o modelo tem sido aplicado. Como todo modelo, este também apresenta limitações no seu domínio de aplicabilidade: em vários casos reais de formação de agregados, não existe a semente fixa e os agregados individuais também se movem simultaneamente. Um exemplo disso ocorre no caso da deposição de poeira, cuja dimensão fractal (espacial) fica em tomo de 1,7. Várias generalizações desse modelo são também possíveis; assim, pode-se, por exemplo, atribuir probabilidades diversas para a partícula grudar ou não em uma partícula vizinha.
Modelo de junção de agregados
Neste modelo, criado por P. Meakin, M. Kolb, R. Botet e R. Julien, em 1983[12], as partículas são inicialmente distribuídas ao acaso em uma rede de pontos e passam a se deslocar aleatoriamente sobre ela. Quando se encontram, elas se fundem formando agregados cada vez maiores (Figura 30). O processo termina quando se tem um único agregado final. A dimensão fractal das estruturas produzidas por esse processo é 1,45 (no plano) e 1,75 (no espaço).
 |
| FIGURA 30 - Figura construída pelo método de junção de agregados |
A dimensão fractal dos agregados tem importância em muitos fenômenos físicos; por exemplo, nos fenômenos de absorção e dispersão da luz pelas partículas suspensas na atmosfera. Michael Berry, em 1989, calculou que a queda dessas partículas, quando dotadas de dimensões fractais não-inteiras, é mais lenta do que a queda de partículas sólidas[13]. Por exemplo, um agregado com mil grãozinhos esféricos, com dimensão fractal d = 1,8, cai dez vezes mais lentamente do que se eles estivessem compactados em uma esfera com d = 3. Isso pode levar a um inverno nuclear muito mais prolongado do que o estimado anteriormente, em situações em que ocorram lançamentos de grande número de partículas na atmosfera.
IFS (Iterated Function Systems)
Este é um procedimento de geração de estruturas fractais baseado em operações da geometria clássica: translação, rotação, contração, etc. Vamos iniciar com o exemplo de um joguinho simples e ilustrativo: comece escolhendo um triângulo eqüilátero em um plano. Marque os vértices A, B e C do triângulo e um ponto P qualquer no seu interior. Agora escolha aleatoriamente um dos vértices A, B ou C. Se o vértice B for o escolhido, mova o ponto P para o ponto médio entre sua posição inicial e o vértice B. Repita o processo, escolhendo aleatoriamente um novo vértice a cada vez. Uma seqüência de pontos, que pode ser facilmente calculada por um microcomputador e representada no monitor, será obtida por esse processo dinâmico. Quando esse joguinho é implementado, uma surpresa: a figura final que aparece (se desprezados alguns pontos iniciais da fase transiente do processo) é um fractal bem conhecido: o Triângulo de Sierpinsky (Figura 31). Esse fractal pode ser obtido também por vários outros processos e sua dimensão fractal, como você poderá verificar, vale dcap = log(3)/log(2).
Uma pergunta que se pode formular é: quais as operações matemáticas que estão subjacentes a esse jogo ou a procedimentos similares? O que se está fazendo é efetuar, em seqüência, um conjunto de transformações {Wi} no plano (transformações lineares e que preservam as linhas retas), com a forma:
 |
(3) |
A transformação será uma contração se a2 + c2 < 1, b2 + d2 < 1 e a2 + b2+ c2 + d2 < 1 + (ad - cb)2. Um conjunto Wl, W2, W3,... de transformações contrativas desse tipo constitui um sistema de funções iteradas (IFS). Atribui-se a cada uma dessas transformações uma determinada probabilidade. Se o resultado médio final dessas operações for contrativo, a figura inicial tenderá para uma figura final, de área menor que a inicial, o atrator. As transformações {Wi} dão a geometria, e as probabilidades {Pi} fornecem a medida (distribuição dos pontos no atrator).
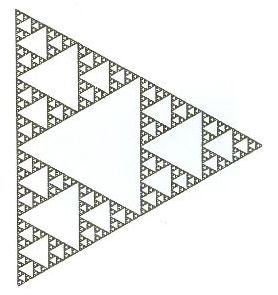 |
| FIGURA 31 - Triângulo de Sierpinsky |
Os modelos IFS têm produzido muitas modelagens interessantes de formas naturais: nuvens, plantas, paisagens, etc., dependendo da escolha das regras e das probabilidades associadas. Um exemplo é exibido na Figura 32, onde uma folha é construída no computador por esse processo. Esses modelos têm encontrado aplicações nas modelagens de objetos e de paisagens em computação gráfica, sendo utilizados em filmes, especialmente de ficção científica (um exemplo é o filme Star Wars). Outra aplicação interessante e útil ocorre no domínio da compressão de imagens, onde vários procedimentos daí decorrentes ajudam a compactar imagens com maior eficiência.
Resultados particularmente significativos sobre os IFS foram demonstrados por Barnsley e outros, em 1985[3]. Um dos teoremas afirma que cada IFS está associado com um único fractal. Outro, denominado teorema da colagem, permite que se analise o procedimento inverso de se construir uma imagem dada qualquer (que chamaremos de figura alvo) a partir de um processo de IFS. O teorema resulta no seguinte: ao se cobrir a figura alvo A, da melhor maneira possível, com cópias transformadas dela mesma, o atrator de um IFS que usa essas mesmas transformações será 'visualmente' próximo da figura-alvo A.
 |
| FIGURA 32 - Estrutura de uma folha gerada por um processo IFS |
APLICAÇÕES DOS FRACTAIS
Usam-se modelos com estrutura fractal para representar ou descrever muitos processos naturais em vários domínios da ciência, da física à biologia, da geologia à astrofísica. A seguir,mencionamos apenas algumas dessas aplicações, sem entrar em qualquer detalhe sobre os processos físicos envolvidos em cada caso. O leitor interessado em conhecer inúmeros outros campos e domínios nos quais os fractais têm sido utilizados poderá consultar a referência 14.
Na física dos materiais ocorrem muitas das principais aplicações dos fractais. O crescimento de estruturas, sejam elas cristais ou a penetração de um fluido em outro material, assumem, com freqüência, estruturas ramificadas com a propriedade de auto-similaridade. O estudo dos meios porosos, que tem repercussões tecnológicas e econômicas, mostra também a presença de fractais. Um exemplo ocorre nos trabalhos de prospecção de petróleo: a rocha na qual o petróleo reside apresenta estrutura porosa com propriedades fractais. Outra área particular de pesquisa se dá através da difração de ondas por superfícies fractais, o que permite, num processo inverso, que se adquiram informações sobre a estrutura da superfície. A superfície dos materiais é, em geral, bastante irregular e pode ter sua dimensão fractal mensurada; esse conhecimento pode vir a ser útil, por exemplo, no estudo dos fenômenos de corrosão.
Muitos fenômenos geológicos possuem a simetria de escala; exemplos disso são as distribuições de freqüência dos tamanhos de fragmentos de rochas, falhas geológicas, terremotos, erupções vulcânicas e depósitos minerais e de petróleo[7]. Uma distribuição fractal requer que o número de objetos maiores que um determinado tamanho (magnitude) tenha uma dependência com esse tamanho que corresponde a uma lei de potência. Um exemplo interessante, já percebido em 1954, é a relação de Gutenberg-Richter entre a magnitude e a freqüência dos terremotos, que leva a uma dimensão fractal de 1,8 aproximadamente. Os fractais têm também se mostrado úteis no estudo dos meandros dos rios e dos contornos das formações geológicas (Figura 33). A dimensão fractal é uma medida da rugosidade da paisagem, e a topografia da Terra é resultado de muitas influências em competição; há evidências, por exemplo, de que o processo de erosão é invariante de escala.
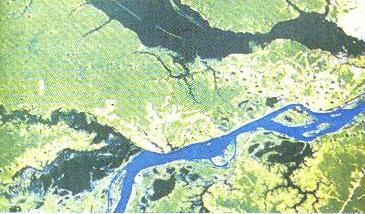 |
| FIGURA 33 - Foto de um satélite: Manaus, na confluência dos rios Solimães e Negro |
O estudo dos processos de fragmentação tem importância teórica e experimental, além de ter aplicações tecnológicas. A fragmentação envolve o início e a propagação de fraturas, um processo altamente não-linear. Existem muitos aspectos fractais nesses processos, já que, muitas vezes, os fragmentos são produzidos dentro de uma gama grande de tamanhos que não estão associados a nenhum comprimento característico natural. Uma lei empírica, usada com freqüência para analisar a produção de pedaços em um processo de fragmentação, tem a forma de uma lei de potência: N(>m) ~ m-d, onde N(>m) é o número de fragmentos com massa maior que m. A constante d é equivalente à dimensão fractal.
Em astrofísica e cosmologia, um problema importante é a distribuição de galáxias no Universo. Aliada a ele, uma pergunta interessante tem, desde muitos séculos, intrigado os cientistas: por que o céu à noite é escuro? Se o Universo fosse infinito e constituído de infinitas estrelas, distribuídas homogeneamente, poder-se-ia mostrar (tente descobrir como) que o céu ficaria claro à noite. Esse paradoxo é denominado de Paradoxo de Olbers, embora outras pessoas já o tivessem discutido antes dele. Ao longo dos séculos, várias respostas parciais foram sendo propostas para o paradoxo[15]. Uma delas supõe que as galáxias estão distribuídas de uma forma fractal; pode-se mostrar que, se a dimensão fractal da distribuição de galáxias for menor que 2, o paradoxo fica resolvido. Existem outras soluções físicas para o paradoxo, mas, é interessante destacar que as últimas medidas da distribuição das galáxias no Universo, que é mais ou menos isotrópica, atribuem um valor aproximado de 1,2 para sua dimensão fractal, pelo menos dentro de domínios menores que 100 milhões de anos-luz (Figura 34).
 |
| FIGURA 34 – Distribuição das galáxias |
Na análise matemática, o uso de funções com propriedades fractais remonta a Riemann e a Weierstrass que, na segunda metade do século passado, construíram funções sem derivadas. Weierstrass definiu a seguinte função contínua, mas que não possui derivada em nenhum ponto:
| (4) |
Uma aplicação que desperta interesse militar é o reconhecimento de imagens. Parte-se aqui da idéia de que os objetos artificiais são construídos em geral a partir de formas regulares, enquanto que os objetos e paisagens naturais têm, via de regra, uma estrutura. irregular, mais próxima dos fractais. Com isso, em fotografias aéreas pouco claras, a identificação de domínios fractais poderia discernir entre objetos naturais e objetos artificiais camuflados.
Usos interessantes dos fractais têm ocorrido em áreas tão diversas como a composição musical. Músicas fractais foram compostas, atribuindo-se, por exemplo, notas e ritmos às cores de figuras fractais emanadas de regras não lineares simples, como o Conjunto de Mandelbrot. A música usual possui uma estrutura de lei de potência que é, portanto, similar àquela apresentada pelos fractais. Embora até agora nenhuma das composições fractais tenha superado o compositor mais medíocre, elas possuem uma mistura de harmonia (ordem) e variedade (caos), que são qualidades presentes na música. De um ponto de vista mais físico, o da acústica, modos de vibração de um tambor particular, com bordas fractais, foram também estudados recentemente.
O Quadro 2 traz uma relação de várias estruturas observadas na natureza com suas correspondentes dimensões fractais, medidas com aproximações variáveis, dentro do domínio de escalas em que a propriedade de similaridade está presente (em geral, apenas em caráter estatístico). Uma visita a um jardim botânico, uma excursão a uma floresta ou paisagem montanhosa ou ainda um mergulho em mares tropicais nos permitirão discernir muitas estruturas fractais na natureza, desde que estejamos possuídos por uma visão 'fractal' (Figura 35).
QUADRO 2 - Dimensões fractais aproximadas de vários processos naturais
| ÁREA |
SISTEMA |
DIMENSÃO FRACTAL |
| BIOLOGIA |
Olho humano Pulmão Cérebro dos mamíferos Ramificação de plantas Proteínas Colônias de fungos e bactérias |
~1,7 ~2,2 ~2,6 2,2 < d < 2,8 1,6 < d <-2,4 ~1,4 (borda) |
| GEOCIÊNClAS |
Linhas costeiras Meandros de rios Contornos topográficos de montanhas Objetos fragmentados (granito, carvão, basalto, quartzo etc.) |
1,2 < d < 1,4 1 < d < 1,2 1,1 < d < 1,3
2,1 < d < 2,6 |
| COSMOLOGIA |
Distribuição de galáxias no Universo |
~1,2 |
| ESTRUTURA DA MATÉRIA |
Nuvens (projeção do perímetro) Aglomerados de metal em catodo Dedos viscosos (produzidos pela injeção de um líquido em outro viscoso) |
~1,35 ~2,43 ~1,7 |
Talvez aqui seja o lugar para fazermos um alerta importante: embora significativo, o cômputo da dimensão fractal ou, melhor dizendo, das dimensões fractais de um conjunto, objeto ou processo dinâmico não carrega em si a informação sobre o mecanismo físico subjacente que gerou aquela estrutura, embora possa trazer indicações naquela direção. Nesse sentido, é bom que se tome cuidado com as 'explicações' superficiais, decorrentes de modismos, presentes às vezes em artigos científicos, livros de divulgação ou em jornais e revistas, de que os fractais seriam a explicação última acerca de qualquer fenômeno 'irregular' da natureza. Os limites dos conceitos e teorias físicas e matemáticas, fontes importantes de analogia para outros domínios da ciência, nem sempre são adequadamente reconhecidos. A utilidade científica dos fractais não deve nos impedir. de ver que eles têm sido freqüentemente extrapolados e usados em outros contextos, sem os devidos cuidados críticos e delimitativos, e que esse processo está, muitas vezes, escorado em determinados interesses econômicos e ideológicos.
 |
| FIGURA 35 - Embrião de pinto |
LIGAÇÕES DOS FRACTAIS COM OS SISTEMAS CAÓTICOS E COMPLEXOS
Vimos que muitos fractais são provenientes de operações não-lineares. Existe, portanto, uma relação bastante íntima entre eles e os sistemas dinâmicos não-lineares; estes sistemas apresentam, em geral, comportamentos caóticos e complexos. Mencionaremos, de forma superficial, alguns desses pontos de interface, muitos dos quais ainda não estão claramente entendidos e são pontos atuais de intensa pesquisa.
Dimensão fractal de atratores
Uma importante caracterização dos atratores caóticos é fornecida pela sua dimensão fractal (ou, mais precisamente, pelo seu espectro de dimensões). Um exemplo é o cômputo da capacidade do Atrator de Lorenz, um modelo paradigmático de atrator caótico; seu valor é de aproximadamente 2,1. Essa dimensão permite quantificar o grau de ocupação com que o atrator preenche o espaço de três dimensões e mostra que ele não pode estar contido em uma superfície.
Bacias fractais
Um fenômeno muitas vezes existente nos sistemas caóticos e complexos, e que tem significativas repercussões em processos evolutivos, é a existência de atratores múltiplos, ou seja, o sistema possui vários atratores para os mesmos valores dos parâmetros. As condições iniciais determinarão para qual atrator o sistema tenderá. Uma situação relativamente comum é aquela em que as fronteiras dessas bacias de atração são fractais. Pode ocorrer também que as próprias bacias se tomem extremamente entrelaçadas e sejam elas mesmas estruturas fractais. Isso tem implicações profundas na previsibilidade do comportamento futuro do sistema, quando se tenta prever para qual atrator ele convergirá ao longo do tempo: se as bacias foram muito entrelaçadas, tal previsão ficará bastante limitada.
Mesmo mapas unidimensionais simples podem apresentar bacias fractais[16]. Um exemplo bidimensional interessante ocorre no chamado mapa do triângulo: trata-se de um mapeamento não-linear no plano, analisado por Yorke e seus colegas[17], no qual existem seis atratores em competição (que, neste caso, são determinados segmentos de reta) e com bacias muito entrelaçadas. A Figura 36 mostra as bacias de atração para cada um dos atratores. Note-se que essas figuras não são interessantes apenas por seu aspecto estético.
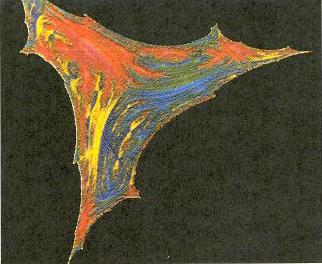 |
| FIGURA 36 – Bacias fractais do mapa do triângulo |
As cores e sua distribuição carregam informações sobre toda a dinâmica do sistema. Tais figuras constituem-se em uma generalização dos gráficos tradicionais, em que a informação está contida apenas na curva (linha unidimensional) do gráfico de uma variável em função de outra. Já nessas figuras toda a área do papel é importante, pois condensa, em cada ponto, informações sobre o sistema (Figura 37).
 |
| FIGURA
37 – Trajetórias de períodos diferentes para um pêndulo forçado.
[Grupo de Caos – Universidade de Maryland] |
Conjuntos de Julia e de Mandelbrot
Estruturas matemáticas interessantes emergiram do estudo do comportamento dos mapeamentos quando se usam números complexos. O exemplo mais importante surgiu com os chamados Conjuntos de Julia e com o Conjunto de Mandelbrot, uma figura muito bonita e dotada de grande riqueza matemática. Vamos apenas descrever como podem ser construídos; o livro de Peitgen e Richter[2] pode ser consultado para maiores detalhes.
Vamos considerar uma iteração quadrática no plano complexo, com a forma Zi+1 = Zi2 + C, ou seja:
| (5) |
Conjuntos de Julia. São os conjuntos constituídos pelos pontos que não tendem nem para zero nem para o infinito. A dinâmica dentro deles é caótica. São obtidos fazendo-se o ponto inicial Z0 fixo e variando-se C. Uma maneira para determinar um conjunto desse tipo é a seguinte: desenham-se todos os pontos que, sob iteração, não escapam para infinito. A fronteira desse conjunto é um Conjunto de Julia (Figura 38).
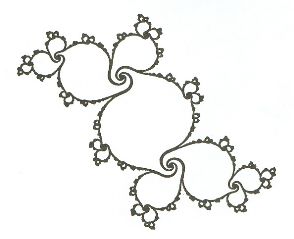 |
| FIGURA 38 – Conjunto de Julia |
Conjunto de Mandelbrot. Nesse caso tomamos C fixo e variamos Z0. O Conjunto de Mandelbrot (Figura 39) é o conjunto de pontos Z0, no plano complexo, para os quais os Zi sucessivos não tendem para infinito. Para determiná-lo, podemos proceder da seguinte maneira: para C = O, por exemplo, faz-se a iteração (5), para cada Z0 e coloca-se cor branca nos pontos em que Z tende para infinito e preta se isto não ocorre. A fronteira do Conjunto de Mandelbrot tem dimensão fractal igual a 2.
O conjunto pode receber também uma estrutura a cores, que contém informações sobre a rapidez com que os pontos tendem para infinito. As cores diferentes são atribuídas aos pontos iniciais de acordo com o número de iterações necessárias para se atingir um certo raio grande, anteriormente definido. O Conjunto de Mandelbrot é um tipo de "dicionário" dos Conjuntos de Julia.
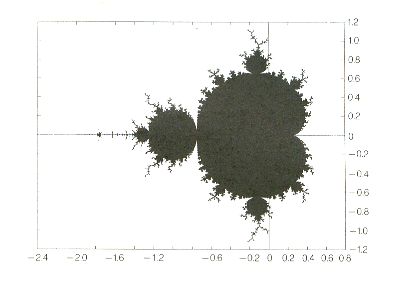 |
| FIGURA 39 - Conjunto de Mandelbrot |
Os pontos que pertencem ao Conjunto de Mandelbrot geram conjuntos de Julia conexos. Os pontos fora dele geram Conjuntos de Julia (fractais) constituídos de pontos isolados. Com iterações similares às de Mandelbrot, no plano complexo, muitas figuras bizarras podem ser construídas, lembrando estruturas naturais com forma de insetos, plantas, paisagens, etc. (Figura 40).
 |
| FIGURA 40 - Imagem fractal tridimensional |
Outras questões significativas
Muitos temas novos de pesquisa na física e na matemática têm utilizado os conceitos da geometria fractal. Do ponto de vista matemático, menciono apenas dois exemplos. No primeiro deles, no estudo da integrabilidade, verifica-se que as singularidades móveis (que aparecem quando equações diferenciais não-lineares são analisadas no plano complexo) de sistemas de equações diferenciais que são não-integráveis apresentam, com freqüência, uma distribuição complicada no plano complexo; existe a conjectura de que essas distribuições são fractais[18]. Um outro ponto matemático, recentemente estudado, diz respeito às relações entre a geometria fractal e a teoria clássica da computação. Existem aí problemas da categoria dos indecidíveis, como, por exemplo, testar se um atrator de um IFS e um dado segmento de linha se interceptam[19]. Isso significa que não existem algoritmos que possam responder a certas questões simples sobre fractais.
Com a introdução e o uso dos fractais na física, inúmeras questões e aplicações novas têm surgido, entre elas as que buscam estabelecer conexões entre a estrutura fractal e o comportamento dinâmico de sistemas caóticos e complexos. Citemos três questões particularmente importantes:
1. A construção de modelos adequados para se descrever a turbulência é um dos grandes problemas da física; embora um avanço significativo tenha sido conseguido com as novas técnicas experimentais e com a introdução de muitos conceitos provenientes do estudo dos sistemas caóticos, o problema parece ainda longe de uma solução geral aceitável. Como outras equações básicas da física, as equações dos fluidos, como as de Euler,por exemplo, podem exibir simetria de escala. Além disso, os fluxos turbulentos devem ser tratados estatisticamente e seus espectros apresentam freqüentemente estrutura fractal Existe a conjectura de Mandelbrot de que as soluções das equações básicas da turbulência envolveriam singularidades que são conjuntos fractais [1(b)].
2. Outra questão bastante discutida nos últimos tempos, e ainda sem uma resposta definitiva, se refere à relação entre os fractais e os ruídos chamados de ruídos l/fα, que apresentam uma lei de potência na sua distribuição espectral (em geral, 0,5 < a < 1,5). Por exemplo, um corte ao longo de uma direção de uma paisagem fractal produz a curva de um gráfico com ruído l/fα. Uma distribuição desse tipo reflete a presença da simetria de escala e a toma, em princípio, aplicável a fenômenos que não possuem comprimento característico[20]. Os fenômenos críticos são também associados com fractais e caos e o conceito de criticalidade auto-organizada foi introduzido para tentar entender os sistemas que tendem naturalmente para uma situação crítica[21]. No estado crítico não há uma escala natural de comprimento e a estatística fractal se aplica. Os sistemas complexos existem no limiar do caos, onde situações críticas ocorrem e a lei de potência predomina. Muitos modelos que obedecem à lei de potência têm sido construídos e estudados: terremotos, avalanches, freqüência no uso de palavras, atividade solar, inversões no campo magnético da Terra, ruídos em circuitos eletrônicos, etc[20]. Uma questão cabível é: existe algum mecanismo universal para gerar ruídos desse tipo? Um possível mecanismo é o da criticalidade auto-organizada. Os fractais e o ruído l/fα a seriam, segundo a conjectura, as marcas espacial e temporal da criticalidade autoorganizada[21]. É mais provável; no entanto, que vários mecanismos genéricos existam e conduzam a esses fenômenos possuidores de simetria de escala. Mas as questões gerais sobre qual o significado da lei de potência e sua relação com os fractais, por que muitas formas naturais têm estrutura fractal e por que o ruído l/fα é prevalente em muitos processos dinâmicos da natureza, permanecem questões substantivas que aguardam respostas mais precisas.
3. Uma terceira área interessante de aplicação dos fractais se refere à construção de urna termodinâmica dos multifractais[22]. Em particular, existem interfaces entre esse estudo e as chamadas wavelets (que fornecem um tipo de generalização da análise de Fourier). Inspirado também na definição de dimensão fractal generalizada, Tsallis introduziu, em 1988[23], uma definição mais geral de entropia, que poderá ser útil em determinados contextos físicos. Nessa seqüência de idéias, a definição do expoente de Lyapounov também pode ser estendida para permitir a análise da taxa média de afastamento (ou aproximação) de trajetórias vizinhas, mesmo nos casos em que o expoente usual de Lyapounov é nulo. Isso significará que essa taxa não é exponencial e obedece a uma lei de potência, como ocorre no limiar do caos, com os sistemas complexos. Estruturas fractais, já presentes no cômputo dos expoentes usuais, poderão surgir também aqui.
Como iniciei o texto com Langevin, terminarei, após este sobrevôo ligeiro sobre conceitos matemáticos e físicos referentes aos fractais, com urna frase também instigante de Spinoza: "Não atribuo à natureza nem beleza nem deformidade, nem ordem nem confusão; é somente do ponto de vista de nossa imaginação que dizemos que as coisas são bonitas ou feias, ordenadas ou caóticas".
Quando nos deparamos com o caráter estranho e abstrato de muitas das novas idéias, como, por exemplo a da existência de dimensões fracionárias, considerações como as de Langevin e de Spinoza podem nos inspirar ou, até mesmo, consolar.
APÊNDICE
ALGUNS PERSONAGENS E SUAS CONTRIBUIÇÕES PIONEIRAS NO ESTUDO DOS FRACTAIS
|
MATEMÁTICA |
FÍSICA |
|
B. Riemann e K. Weierstrass Curvas que são contínuas mas que não têm derivada em nenhum ponto (1862, 1872) |
J. H. Lambert e J. F. W. Herschel Modelo
de universo hierárquico (fractal) |
|
H. J. Smith e G. Cantor Conjunto de Cantor (1875, 1883) |
R. A. Proctor e E. E. Fournier d'Albe Aglomerados galácticos em níveis hierárquicos (1871, 1907) |
|
G. Peano Curvas que preenchem o plano (1890) |
J. Perrin Experimentos com movimento browniano. Filosofia das curvas irregulares (1909) |
|
H. von Koch Curva de Koch (1904) W. Sierpinsky Triângulo de Sierpinsky (1916) Wada Bacias fractais (1917) |
C. V. L. Charlier, F. Selety, E. Borel, M. Amoroso Costa e P. Lévy Universos newtonianos infinitos, fractais, com densidade média nula e com potencial gravitacional finito (1922) |
|
F. Hausdorff e A. S. Besicovitch Idéia de dimensão fractal (1919, 1935) |
L. F. Richardson Turbulência envolve uma 'cascata' de energia de grandes para pequenos vórtices (1922). Comprimento das linhas costeiras (1961) |
|
P. Fatou e G. Julia Conjuntos obtidos por iterações no plano complexo (1918, 1919) |
A. N. Kolmogorov Auto-similaridade e 'cascata' de energia na turbulência (1941) |
|
B. Mandelbrot A geometria fractal da natureza (1975) |
|
NOTAS BIBLIOGRÁFICAS
1. MANDELBROT, B. The fractal geometry of nature. Nova York: W. H. Freeman, 1983.[volta(a)] [volta(b)]
2. PEITGEN, H.-O.; RICHTER, P. The beauty of fractals. Nova York: Springer-Verlag, 1986.[volta]
3. BARNSLEY, M. Fractals everywhere. Nova York: Academic Press, 1988.[volta]
4. FLEISHMANN, M.; TILDESLEY, D.; BALL, R. C. (org.). Fractals in the natural sciences. Princeton: Princeton University Press, 1989.[volta]
5. STEWART, I. Será que Deus joga dados? A nova matemática do caos. Rio de Janeiro: Jorge Zahar Editor, 1991.[volta]
6. PEITGEN, H.-O.; JÜRGENS, H.; SAUPE, D. Chaos and fractals - new frontiers of science. Nova York: Primavera-Verão, 1992.[volta]
7. TURCOTTE, D. L. Fractals and chaos in geology and geophysics. Nova York: Cambridge University Press, 1992.[volta]
8. FIELD, M.; GOLUBITSKY; M. Symmetry in chaos. Oxford: Oxford University Press, 1992.[volta]
9. WEGNER, T.; TYLER, B. Criando fractais. Rio de Janeiro: Axcel Books do Brasil, 1995. (O livro contém o Fractint - programa de domínio público sobre fractais, também disponível na rede).[volta]
10. Ciência Hoje. Diversos artigos tratam de fractais, caos e sistemas complexos: 7, n. 38, 24 (fractais); 10, n. 55, 26 (fenômenos de agregação); 14, n. 80 (número especial sobre o caos); 15, n. 90 (avalanches); 16, n. 92, 14 (sistemas complexos); 17, n. 102, 26 (sincronização e controle do caos).[volta]
11. WITTEN, T. A.; SANDER, L. M. Phys. Rev. B27, p. 5.686, 1983.[volta]
12. MEAKIN, P.. Phys. Rev. Lett. 51, p. 1.119, 1983; KOLB, M.; BOTET, R.; JULIEN, R. Phys. Rev. Lett. 51, p. 1.123, 1983.[volta]
13. BERRY, M. Physica D38, p. 29, 1989.[volta]
14. HURD, A. J. Resource Letter - fractals. American Journal of Physics 56, p. 969, 1988.[volta]
15. HARRISON, E. A escuridão da noite. Rio de Janeiro: Jorge Zahar Editor, 1995.[volta]
16. LIMA, A. S.; MOREIRA, I. A.; SERRA, A. M. Phys. Lett. Al90, p. 403, 1994; MOREIRA, I. C.; Naturforsch , Z. 51a, p. 1.175, 1996.[volta]
17. ALEXANDER, 1. c.; HUNT, B. R; KAN, 1.; YORKE, J. A. Ergod. Th and Dynam. Sys. 16, p. 651, 1996.[volta]
18. BOUNTIS, T. Int. J. Bif. and Chaos 2, p. 217, 1992.[volta]
19. DUBE, S. Complex Systems 7, p. 423, 1993.[volta]
20. WEST, B. J.; SHLESINGER, M. American Scientist, 78, p. 40, 1990.[volta]
21. BAK, P.; CHEN, K. Physica D38, p. 5, 1989.[volta]
22. MCCAULEY, J. L. Phys. Rep. p. 189, p. 225, 1990.[volta]
23. TSALLIS, C.; J. Stat. Phys. 52, p. 479, 1988.[volta]