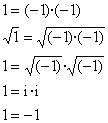Profe Cossoli

¿Sabías que...?

Sobre Matemática - Parte II

"Cuanto más conozcas, mejor"

Volver al Índice

El texto que sigue está reproducido literalmente del libro de N. Estevanez:" Entretenimientos Matemáticos, Físicos, Químicos, etc.".

Cuando un matemático oriental inventó el admirable juego de ajedrez, quiso el monarca de Persia conocer y premiar al inventor. Y cuenta el árabe Al-Sefadi que el rey ofreció a dicho inventor concederle el premio que solicitara.

El matemático se contentó con pedirle 1 grano de trigo por la primera casilla del tablero de ajedrez, 2 por la segunda, 4 por la tercera y así sucesivamente, siempre doblando, hasta la última de las 64 casillas.

Es decir 1 (= 2⁰) + 2 (= 2¹) + 4 (= 2²) + 8 (= 2³) + 16 (= 2⁴) +..   ...   .. + 2⁶⁴

El soberano persa casi se indignó de una petición que, a su parecer, no había de hacer honor a su liberalidad.

- ¿No quieres nada más? preguntó.
- Con eso me bastará, le respondió el matemático.

El rey dio la orden a su gran visir de que, inmediatamente, quedaran satisfechos los deseos del sabio.

¡Pero cuál no sería el asombro del visir, después de hacer el cálculo, viendo que era imposible dar cumplimiento a la orden!

Para darle al inventor la cantidad que pedía, no había trigo bastante en los reales graneros, ni en los de toda Persia, ni en todos los de Asia.

El rey tuvo que confesar al sabio que no podía cumplirle su promesa, por no ser bastante rico.

Los términos de la progresión arrojan, en efecto, el siguiente resultado: diez y ocho trillones, cuatrocientos cuarenta y seis mil setecientos cuarenta y cuatro billones, setenta y tres mil setecientos nueve millones, quinientos cincuenta y un mil seiscientos quince granos de trigo:

¡¡¡ 18.446.744.073.709.551.615 !!!

Sabido es que una libra de trigo, de tamaño medio, contiene 12.800 granos aproximadamente. ¡Calcúlese las libras que necesitaba el rey para premiar al sabio! Más de las que produciría en ocho años toda la superficie de la Tierra, incluyendo los mares.

Con la cantidad de trigo reclamada, podría hacerse una pirámide de 14,48 km de altura  y 14,48 km de longitud por 14,48 km de latitud en la base; o bien una masa paralelipípeda de 46,76 km cuadradas en su base, con 5,19 km de altura.

Para comprar esa cantidad de trigo, si la hubiera, no habría dinero bastante en este mundo.

 

Tomado de solidaridad (Agregar www. al principio y .net al final)

Aún en las etapas más primitivas de la evolución humana se encuentra en el hombre una facultad que llamaremos, a falta de mejor denominación, el sentido del número. Esta facultad le permite reconocer que algo ha cambiado en una pequeña colección, cuando, sin su conocimiento directo, se ha sacado o añadido un objeto.

El sentido del número no debe ser confundido con la facultad de contar, que es probablemente mucho más reciente y que implica un proceso mental bastante más complicado. Contar es, en la medida de nuestros conocimientos actuales, un atributo exclusivamente humano, mientras que algunas especies de animales parecen poseer un rudimentario sentido del número parecido al nuestro. Tal es, por lo menos, la opinión de observadores competentes de las costumbres de los animales, y su teoría se apoya en una gran cantidad de comprobaciones.

Muchos pájaros, por ejemplo, poseen ese sentido del número. Si un nido contiene cuatro huevos, se puede sacar de él un huevo sin que nada ocurra, pero en general, el pájaro lo abandonará si se sacan dos: en alguna forma inexplicable el pájaro puede distinguir dos de tres. Pero esta facultad no está reservada exclusivamente a los pájaros, en efecto, el caso más notable que conocemos es el del insecto llamado "avispa solitaria". La avispa madre deposita sus huevos en sendas celdillas y provee a cada huevo de un cierto número de orugas vivas, de las que se alimentarán las larvas al nacer. Ahora bien, la cantidad de víctimas es notablemente constante, para cada una d en las especies de esta avispa; unas suministran cinco, otras doce y algunas hasta 24 orugas por celda. Pero lo más asombroso es lo que ocurre con el género Eumenus, en el que el macho es bastante más pequeño que la hembra. De alguna manera misteriosa, la madre sabe si el huevo producirá un macho o una hembra, y suministra a cada celda el alimento necesario sobre el caso, no cambia ni la especie ni el tamaño de las orugas, pero pone cinco orugas si el huevo corresponde a un macho y diez si corresponde a una hembra.

La regularidad del comportamiento de la avispa y el hecho de que esté relacionado con una función fundamental de la vida del insecto hacen que este caso resulte menos convincente que el que sigue, en el que la conducta de un pájaro parecería lindar con lo intencional:
Un terrateniente estaba decidido a matar a un cuervo que había hecho su nido en el mirador de la finca. Repetidas veces había intentado sorprender al pájaro, pero en vano; cuando el hombre se aproximaba, el cuervo abandonaba su nido para posarse a la expectativa en un árbol distante y no volvía al mirador hasta que el hombre se hubiera alejado. Un día el propietario recurrió a un ardid: dos hombres entraron en la torre; uno quedó dentro y otro salió y se alejó, más el pájaro no se dejó engañar y esperó hasta que el segundo hubo salido a su vez. El experimento se repitió los días siguientes con 2, 3 y 4 hombres, pero siempre infructuosamente. Por fin, 5 hombres entraron en la torre y 4 de ellos después salieron, mientras el quinto quedaba adentro. Entonces el pájaro perdió la cuenta, incapaz de distinguir entre 4 y 5, volvió enseguida a su nido.

(Fragmento del libro "El número, lenguaje de la ciencia" de Tobías Dantzig).

Tomado de ar.geocities (Agregar http:// y .com/matematicamente al final)

La naturaleza es muy repetitiva; está llena de ritmos, de períodos, de latidos, de ciclos. En la repetición de los días, las estaciones, los años, hay buenos ejemplos.

Tales repeticiones o iteraciones se pueden estudiar muy cómodamente hoy en día con la ayuda de la computadora o de la calculadora. Por eso se ha desarrollado mucho recientemente una interesante teoría matemática, "la teoría de la iteración". Con la computadora se puede formar rápidamente la sucesión de resultados de aplicar un proceso iterativo. Con muchas repeticiones que la computadora nos hace nos podemos formar una idea sobre el modo cómo el proceso funciona. Luego tratamos de asegurarnos de que las cosas son en realidad como nuestra idea previa afirma.

La teoría de la iteración tiene muchas aplicaciones interesantes. Acá hay un proceso curioso de iteración para que tengas una idea de cómo funciona el estudio, aunque es verdad que esto no parece ser por ahora de los que se apliquen a situaciones de interés:

Toma tu calculadora. Elegí un número cualquiera. Si es par divídelo por dos. Si es impar, multiplícalo por 3. Añadí 1 al resultado (así obtenés un número par) y divídelo en dos. Aplica el mismo proceso al resultado. Otra vez...otra vez...

Tomado de ar.geocities (Agregar http:// y .com/matematicamente al final)

Un año es el período de tiempo que tarda la tierra en dar una vuelta alrededor del sol y aproximadamente consiste en 365 días, 5 horas, 48 minutos y 46 segundos, o sea 365 días y un cuarto menos 11 minutos y 14 segundos. Normalmente se redondea diciendo que dura 365 días y un cuarto.

Los egipcios y los mesopotámicos se pueden considerar como los padres de la ciencia, ya que desde finales del milenio IV a.C., desarrollaron unos conocimientos que sirvieron de base a los griegos. Entre otras cosas, inventaron los primeros sistemas de escritura y los primeros sistemas de numeración estructurados. En Mesopotamia usaban la base de numeración 60, número que debía de ser mágico para ellos y que es la mayor base de la historia. Los egipcios optan por el sistema decimal (base 10), el más frecuente de la historia y el que usamos actualmente. Crearon los primeros calendarios, basados en el ciclo de la Luna (29 días y medio) que es fácil de percibir, obteniendo años de 354 días. Sin embargo, con ese calendario se produce un desfase en las estaciones (ajustadas a los 365 días y cuarto del año solar). Los mesopotámicos crearon un burdo calendario de 12 meses de 29 y 30 días alternos añadiendo un mes cada cierto tiempo para corregir el desfase. Los egipcios reservaron el calendario lunar para la vida religiosa y crearon un calendario civil de 365 días (12 meses de 30 días y 5 días más aparte), que coincide con el período de tiempo entre dos solsticios de verano, entre dos apariciones por el Este de Sirio (Sothis, para los egipcios), época que coincide con la crecida del Nilo.

La semana es, históricamente, una agrupación de días. Los egipcios usaban semanas de 10 días, pero nosotros hemos heredado las semanas de 7 días de los romanos y estos a su vez de los mesopotámicos y la correspondencia de sus nombres con los astros, ya que los romanos designaron cada día al culto a una divinidad:

• Lunes: Del latín dies lunae, día de la Luna. En inglés, Monday, de Moon (Luna).

• Martes: Del latín dies martis, día de Marte (dios de la guerra). En inglés, Tuesday.

• Miércoles: Del latín dies mercuri, día de Mercurio (dios del comercio y de los caminantes, mensajero de los dioses). En inglés, Wednesday.

• Jueves: Del latín Iovis dies, día de Júpiter (dios que fue asimilado al Zeus griego, dios de los dioses). En inglés, Thursday.

• Viernes: Del latín veneris dies, día de Venus (asimilación de la diosa Afrodita griega, diosa del amor y de la belleza). En inglés, Friday.

• Sábado: Día de Saturno (dios de los vendimiadores y campesinos). En inglés, Saturday. Aunque, el nombre de Sábado proviene del latín sabbatum y este del hebreo sabbath, que significa descanso. Este es, históricamente, el séptimo día de la semana y es el que dedican los judíos al descanso, ya que según la Biblia Dios descansó en el séptimo día.

• Domingo: Del latín Dies Dominicus, día del Señor. Los romanos dedicaron este día al Sol. En inglés, Sunday, de Sun (Sol). Históricamente el Domingo es el primer día de la semana. Los cristianos trasladaron el día de descanso al primer día de la semana para conmemorar la Resurrección de Cristo, que tuvo lugar en ese día. No obstante, en la actualidad se considera al Domingo como el séptimo día y existe una recomendación para hacerlo así, del ISO (International Standard Organization, Organización Internacional de Estándares).

 A lo largo de la Historia, ha habido diversos calendarios con los que el hombre ha intentado medir el tiempo. Los más importantes han sido los 3 siguientes, que han sido sucesivas aproximaciones para medir el tiempo en años:

Calendario egipcio: Estaba formado por 12 meses de 30 días, seguidos de una fiesta de 5 días. En total 365 días. Como esa no es la auténtica duración del año, el año se desplazaba casi un cuarto de día al año. Por tanto, con este calendario, en menos de 700 años se notaría que el tiempo cambia y que en invierno hace calor y en verano frío.

Calendario juliano: Introducido por Julio César en el año 46 a.C. resolvió parcialmente el problema del calendario egipcio introduciendo un día extra cada 4 años (años bisiestos). Para compensar el deslizamiento del calendario egipcio, a ese año se le añadieron 2 meses extra, así como 23 días más en Febrero. Así, el año 46 a.C. es el año más largo registrado, con 455 días. Esta mejora también producía desplazamiento de las estaciones, aunque más lentamente (más de 7 días cada 1000 años). Como fundador, Julio César se dedicó un mes a sí mismo, el de Julio, con 31 días. Cuando su sobrino Octavio Augusto se convirtió en emperador de Roma, también se apropió de un mes, el de Agosto, al que le añadió un día más, quitándoselo al mes de Febrero.

Calendario gregoriano: Introducido por el Papa Gregorio XIII en 1582, modifica el juliano evitando los años bisiestos cuando caen en las centenas excepto cuando son divisibles por 4. Así, el año 1900 no fue bisiesto y si lo será el 2000. Cuando se introdujo este calendario se decretó que el día 5 de octubre fuera el 15 de octubre para corregir el desfase entre el calendario juliano y el solar. Por tanto, el año 1582 es el año más corto registrado y se eliminaron, de esta guisa, 10 días de la historia.

 En el mundo hay otros 40 calendarios vigentes, aunque el gregoriano se usa de forma oficial en casi todos los países. Así, por ejemplo, a la llegada del año 2000, el pueblo judío estará en un día cualquiera de mediados del año 5759. Los musulmanes se hallarán en el año 1421. Los hindúes, con su calendario Saka, estarán en 1922.

 Se cree que el calendario gregoriano, que se usa en casi todo el mundo, tiene un error de 4 años. Probablemente el culpable sea un monje escita del siglo VI llamado Dionisio el Exiguo, también conocido como el pequeño Dionisio (se supone que por su tamaño). Este fraile realizó los cálculos en los que se basó la reforma gregoriana (hecha en 1582). Para actualizar el sistema implantado en tiempos de Julio César, tomó como punto de partida el nacimiento de Jesús, que ubicó en el 753 de la fundación de Roma, en vez de en el 749. Es tanto como decir que Cristo nació en el año 4 antes de Cristo. Además, Dionisio el Exiguo utilizó el sistema numérico romano en el que no existía el cero, por lo que situó el inicio de la era en el año 1 (el Anni Domini Nostri Jesu Christi). Por tanto, el año 0 no existió y del año 1 a.C. se pasa directamente al 1 d.C. Por esto, y sin tener en cuenta el desplazamiento de 4 años, tenemos que el nuevo milenio empezará con el siglo XXI el día 1 de Enero del año 2001.

 La elección del 25 de Diciembre como fecha del nacimiento de Cristo obedeció más a criterios religiosos que históricos. Tras barajar varias fechas (28 de Marzo, 2 de Abril, 18 de Noviembre y 6 de Enero), el Papa Liberio en el año 354 optó por fijar la Navidad en el solsticio de invierno para sustituir la festividad dedicada a la diosa Mithra, divinidad del Sol.

 La Pascua de Resurrección es una fiesta de la liturgia cristiana que se celebra en Primavera (con fecha variable), en memoria de la Resurrección de Cristo. Esta fecha es 3 días después del Jueves Santo día en que los cristianos rememoran la muerte de Cristo en la Cruz, ya que las Sagradas Escrituras dicen que "resucitó al tercer día". Toda esa semana es llamada Semana Santa y los cristianos suelen sacar sus imágenes en procesión. El concilio de Nicea (325) estableció a la cristiandad que la fiesta de Pascua debe celebrarse cada año el Domingo siguiente al primer plenilunio tras el equinoccio de Primavera, fijado el 21 de Marzo. Esto hace que la fecha de Pascua esté siempre comprendida entre el 22 de Marzo y el 25 de Abril, ambas incluidas. Karl F. Gauss (1777-1855), afamado y astuto matemático, ideó un método para calcular la fecha exacta en la que celebrar la Pascua de Resurrección. Según la fórmula de Gauss la fecha de Pascua debe ser una de las dos siguientes (la única que exista de las dos):

El (22 + d + e) de Marzo.

El (d + e - 9) de Abril.

Teniendo en cuenta que, si representamos como "x MOD y" el resto de la división entera "x/y", se establece que:

a = año MOD 19

b = año MOD 4

c = año MOD 7

d = (19a + M) MOD 30

e = (2b + 4c + 6d + N) MOD 7

y donde M=15 y N=6 en el calendario juliano. En el calendario gregoriano los valores de M y N varían lentamente y, hasta el año 2100, tienen los siguientes valores: M=24 y N=5. Algunos ejemplos, son los siguientes: En 1988 y en 1994 la Pascua se celebró el 3 de Abril, en 1995 fue el 16 de Abril, en 1996 fue el 7 de Abril, en 1997 fue el 30 de Marzo y en 1998 fue el 12 de Abril.

Otra forma de calcular esta fecha es utilizando el algoritmo de Butcher, del "Almanaque eclesiástico" de 1876, que es válido para el año 1582 y los años posteriores a este:

A = año MOD 19

B = año / 100

C = año MOD 100

D = B / 4

E = B MOD 4

F = (B+8) / 25

G = (B-F+1) / 3

H = (19A + B - D - G + 15) MOD 30

I = C / 4

K = C MOD 4

L = (32 + 2E + 2I - H - K) MOD 7

M = (A + 11H + 22L) / 451

N = H + L - 7M + 114

MES = N / 31

DIA = 1 + (N MOD 31)

Las fechas de Pascua se repiten en idéntica sucesión en un periodo de 5.700.000 años y en ese lapso de tiempo la fecha más frecuente es el 19 de Abril.

 El segundo fue definido en 1967 por la Comisión Internacional de Pesos y Medidas como el tiempo que necesita un electrón para girar sobre su propio eje dentro de un átomo de cesio. El llamado reloj atómico puede medir la longitud de un segundo con una exactitud de 13 cifras decimales. Más exacto aún es el movimiento del electrón en una molécula de hidrógeno que consigue una exactitud de 15 cifras decimales. Por debajo del segundo existen otra unidades: milisegundo (milésima parte de un segundo, 10-3 segundos), microsegundo (millonésima de segundo, 10-6 segundos), nanosegundo (milmillonésima de segundo, 10-9 segundos), picosegundo (billonésima de segundo, 10-12 segundos) y femtosegundo (milbillonésima de segundo, 10-15 segundos).

Tomado de: calidoscopio (Agregar www. al principio y .com al final)

SIGNIFICADO DE LA PALABRA "FALACIA"

Una "falacia" es una afirmación falsa. Si bien tiene una demostración que la apoya, esa demostración contiene algún enunciado claramente falso, pero que al ser colocada entre otras verdaderas pasa desapercibida. En demostraciones de las falacias matemáticas está contenida alguna proposición claramente falsa, el juego está en encontrarla.

2 = 1

 Sea a = b

Multiplicamos por a

a. a = a. b => a² = a b

Restamos - b² en ambos miembros
 

a² - b² = a b - b²

Factoreando tenemos: (a+b)(a - b) = b (a - b)

Dividimos por (a - b) en ambos miembros

 
a+b = b, pero a = b

luego 2b = b

Dividimos por b

Entonces... 2 = 1

1 = 0

(n+1)² = n²+2n+1

 
(n+1)² - (2n+1) = n²

(n+1)² - (2n+1) - n (2n+1) = n² - n (2n+1)

(n+1)² - (n+1) (2n+1) = n² - n (2n+1)

[(n+1)² - (n+1) (2n+1) + (2n+1)²]/4 = [n² - n(2n+1) + (2n+1)²]/4

[(n+1)-(2n+1)/2]2 = [n-(2n+1)/2]2

(n+1)-(2n+1)/2 = n-(2n+1)/2

 
n+1 = n

Si n = 0, Entonces...1 = 0

 

1 = -1

(Requiere conocer números complejos)

Donde: i es la unidad imaginaria

4 = 5

16 - 36 = 25 - 45

16 - 36 + (20 + 1/4) = 25 - 45 + (20 + 1/4)

16 - 36 + (81/4) = 25 - 45 + (81/4)

16 - 36 + (9/2)² = 25 - 45 + (9/2)²

4² - 2 . 4 . (9/2) + (9/2)² = 5² - 2 . 5 . (9/2) + (9/2)²
Factoreando en ambos miembros

(4 - 9/2)² = (5 - 9/2)²

Aplicamos raíz cuadrada en ambos miembros

4 - (9/2) = 5 - (9/2)

Sumamos 9/2 en ambos miembros

Entonces

4 = 5

SIGNIFICADO DEL TÉRMINO "PARADOJAS "

El término paradoja viene del griego (para y doxos) y significa "más allá de lo creíble". En la actualidad la palabra "paradoja" tiene numerosos significados:

1) Afirmación que parece falsa, aunque en realidad es verdadera.
2) Afirmación que parece verdadera, pero en realidad es falsa.
3) Cadena de razonamientos aparentemente impecables, que conducen sin embargo a contradicciones lógicas. (Las paradojas de esta clase suelen llamarse falacias.)
4) Declaración cuya veracidad o falsedad es indecible.
5) Verdad que se vuelve patas arriba para llamar la atención.

Las paradojas matemáticas, como las científicas, pueden ser mucho más que amenidades, y llevarnos hasta nociones muy profundas. A los primeros pensadores griegos les resultaba tan paradógico como insoportable que la diagonal de un cuadrado de lado unidad no pudiera ser medida exactamente por finas que se hicieran las graduaciones de la regla. Este hecho perturbador sirvió para abrir el vasto dominio de los números irracionales. Los matemáticos del siglo pasado encontraban enormemente paradógico que todos los miembros de un conjunto infinito puedan ponerse en correspondencia biunívoca con los miembros de algún subconjunto del dado, mientras por otra parte podían existir conjuntos infinitos entre los cuales es imposible establecer una correspondencia biunívoca. Tales paradojas condujeron a desarrollar la moderna teoría de conjuntos, que a su vez ha ejercido profunda influencia sobre la filosofía de la ciencia. Mucho podemos aprender de las paradojas. Al igual que los buenos trucos de ilusionismo, nos causan tanto asombro que inmediatamente queremos saber como se han hecho. Los ilusionistas no revelan jamás como hacen lo que hacen, pero los matemáticos no tienen necesidad de guardar el secreto.

1) UN ENUNCIADO Y SU CONTRARIO.

"Esta frase consta de siete palabras." Está claro que su enunciado es falso, ya que consta de seis. Por tanto, su contrario debería ser verdadero. ¿Es esto correcto?

2) LA PARADOJA DEL MENTIROSO

Se atribuye a Epiménides haber afirmado: "Todos los cretenses son mentirosos". Sabiendo que él mismo era cretense, ¿decía Epiménides la verdad?

3) LOS TRES ENUNCIADOS FALSOS

Tenemos aquí tres enunciados falsos. ¿Será capaz Ud. de descubrir cuáles?
        1) 2+2=4
        2) 3x6=17
        3) 8/4=2
        4) 13-6=5
        5) 5+4=9

4) ¿APROBARÁ EL EXAMEN?

El siguiente relato ocurrió en un examen oral.

PROFESOR: De las siete preguntas de que consta el examen, ya te has equivocado en tres preguntas, y sólo nos queda una. Tu aprobado o desaprobado (suspenso) depende completamente de si aciertas o no la próxima pregunta. ¿Te das cuenta?
ALUMNO: Sí. Me doy cuenta.
PROFESOR: El estar nervioso no te ayudará.
ALUMNO: Ya lo sé. Trataré de tranquilizarme.
PROFESOR: Y esta es la pregunta. Recuerda: todo depende de si contestas esto bien o mal.
ALUMNO: Sí, sí, ¡ya lo sé!
PROFESOR: La pregunta es ésta: ¿Aprobarás este examen?
ALUMNO: ¿Cómo voy a saberlo?
PROFESOR: Eso no es una respuesta. Debes darme una respuesta clara, sí o no. Si contestas bien, aprobarás; si no, desaprobarás. ¡Así de simple!

 La cuestión no le parecía nada simple al alumno. La verdad es que cuanto más pensaba en ello más confuso se sentía. Y de repente cayó en la cuenta de algo muy interesante. Si contestaba una cosa, el profesor tendría la posibilidad de aprobarle o desaprobarle, como más le complaciera. Si contestaba lo otro, sería imposible que el profesor le aprobara o le desaprobara sin contradecir sus propias reglas. Como el alumno tenía más interés en no desaprobado que en aprobar, eligió la segunda alternativa, y contestó de una manera que confundió por completo al profesor. ¿Qué respuesta dio?

5) UNA DE LAS DOS

He aquí dos afirmaciones. Una de ellas es falsa. ¿Cuál?

6) ERRORES

En este párrafo se cometen tres errores.
        París es la capital de Francia.
        Dos más dos es igual a cinco.
        América fue descubierta en 1.492.
        ¿Cuáles son los errores?

 7)  HORRORES

 En este párrafo se cometen dos errores.
       Roma es la capital de Italia.
       Dos por dos es igual a cinco.
       Hillary escalé el Everest.
       ¿Cuáles son los errores?

 8)  PARADOJA TEMPORAL

Un español en 1.987 llamó por teléfono a otro que se encontraba en 1.986, y le dijo:
         - Mañana te telefonearé de nuevo.
         - De acuerdo. ¡Hasta mañana!
         ¿Podría darse esta situación un tanto paradójica en la vida real?.

9) REGLAS Y LEYES

"Todas las reglas tienen una excepción" . ¿ Será cierto?

10) PARADOJA DE LA TARJETA

El matemático P.E.B. Jourdain, en 1913, propuso la siguiente paradoja: en uno de los lados de una tarjeta se podía leer:

"La oración del otro lado de esta tarjeta es VERDADERA."

En la otra cara estaba escrito:

"La oración del otro lado de esta tarjeta es FALSA."

11) EL PLEITO SOBRE LOS HONORARIOS

La siguiente paradoja lógica se le planteó al filósofo griego Protágoras hace unos 2.400 años aproximadamente. Protágoras fue uno de los precursores del movimiento sofista. Según algunos de sus contemporáneos fue el primero que sostuvo que sobre una misma cuestión existen dos discursos mutuamente opuestos.

Durante años enseñó sus conocimientos a los hijos de las familias pudientes griegas, por los que cobró grandes sumas de dinero. Los cursos eran rápidos y eficaces, y entre las enseñanzas transmitidas gran parte la ocupaban tanto la retórica como la argumentación. Para que tengan una idea, las escuelas sofistas eran, en aquél entonces, lo que hoy pueden ser las universidades privadas. Las enseñanzas de los sofistas eran muy valiosas para aquellos que quisieran hacer carrera política o judicial.

El "pleito de los honorarios" se plantea entre el maestro Protágoras y su discípulo Evalto al que acoge en su academia con la condición de que le pagara los honorarios del curso cuando ganase su primer pleito. Terminado el curso Evalto no tuvo ningún cliente y Protágoras, que era sofista pero no estoico, demandó a su discípulo.

Los argumentos expuestos fueron los siguientes:

Evalto: Tanto si gano como si pierdo, en ningún caso tendré obligación de pagar a Protágoras. Si yo gano el pleito, no tendré que pagar ya que el Juez habrá desestimado la demanda y dirá que no pague. Si lo pierdo, entonces, no habré ganado mi primer pleito y por lo tanto no se habrá cumplido la condición que hacía exigible la obligación de pago de los honorarios.

Protágoras: Tanto si gano como si pierdo este pleito, Evalto siempre tendrá obligación de pagarme. Si yo gano la demanda, por definición tendrá que pagarme pues esta es la cuestión que se ventila en este pleito y el Juez dirá que Evalto me pague. Y si la pierdo, también tendrá que pagarme porque significará que ha ganado su primer pleito; es decir se habrá cumplido la condición de nuestro acuerdo.

¿Quién crees que tenía razón?

SOLUCIONES

1) UN ENUNCIADO Y SU CONTRARIO. ¡Es falso! La oración contraria: "Esta frase no consta de siete palabras." está formada exactamente por siete palabras. ¿Cómo resolver estos raros dilemas?

2) LA PARADOJA DEL MENTIROSO: Es para razonar y discutir...

3) LOS TRES ENUNCIADOS FALSOS. Únicamente son falsos los enunciados 2 y 4. Por tanto, la afirmación de hay tres enunciados falsos es falsa. Tenemos así el tercero de los enunciados falsos. ¿No es verdad?

4) APROBARÁ EL EXAMEN. Supongamos que contestara que sí. En este caso el profesor podría desaprobarle o aprobarle, como prefiriese. Si le desaprobaba y el alumno preguntaba por qué, el profesor podría decir "Contestaste mal la última pregunta, después de todo dijiste que ibas a aprobar y no fue así, y como la última pregunta estaba mal, tienes que desaprobar". Pero el profesor podría igualmente aprobarle y decir "Dijiste que aprobarías, y como ha sido así, tenías razón, así que contestaste bien la última pregunta, y por eso apruebas". Desde luego los dos razonamientos son circulares, pero ninguno de los dos es peor que el otro.
        En cambio, si el alumno contestara que no, el profesor no podría ni desaprobarle ni aprobarle. Si le aprobaba, el alumno habría contestado mal y habría desaprobado. Si le desaprobaba, el alumno habría contestado bien y habría aprobado. Así que el profesor no podía ni aprobarle ni desaprobarle.
        Como el alumno tenía más interés en no desaprobar que en aprobar, contestó "No" y fastidió al profesor por completo.

5) UNA DE LAS DOS. La primera es cierta: hay dos afirmaciones, ella misma y la segunda. ¿Y la otra? Si fuese falsa, ella misma habría de decir que no hay ninguna falsa (al ser falsa) y si fuese verdadera, ¿dónde está la falsa? Por lo que nos introducimos en una clara contradicción.

 6)  ERRORES. Hay dos errores; uno es la frase que dice «Dos más dos es igual a cinco». El otro es: «En este acertijo se cometen tres errores».

 7) HORRORES. Se trata de una paradoja. Si suponemos que el único error es «Dos por dos es igual a cinco», entonces la primera frase debe ser correcta; pero no puede serlo, porque afirma que los errores son dos. Y si suponemos que los errores son, efectivamente, dos, la primera frase debe estar equivocada; pero no puede estarlo, porque afirma precisamente que los errores son tantos como supusimos. Luego este acertijo no tiene solución lógica.

8) PARADOJA TEMPORAL. Por paradójica que parezca es posible con la condición de que el primer español se encuentre en la Península y el otro en las Islas Canarias y que la llamada se realice en la Península después de las 12 de la noche del 31 de diciembre y antes de la una de la madrugada del día 1 de enero.

9) REGLAS Y LEYES: No hay manera de decidirlo, porque si esa afirmación es verdadera, la regla "Todas las reglas tienen una excepción" tendría una excepción. ¿Cuál sería esa excepción?: una regla que no tuviera excepción... pero dijimos que TODAS las reglas tienen una excepción. Mejor sería cambiar el enunciado y decir: " CASI TODAS las reglas tienen una excepción"

11) EL PLEITO SOBRE LOS HONORARIOS El origen de la paradoja reside en el hecho de que tanto Protágoras como su alumno primero aceptan la autoridad del tribunal pero después, si el veredicto no les favorece, deciden no someterse. Dicho de otra manera: más que una paradoja este es un caso de mala fe por parte de maestro y alumno. La finalidad del pleito es resolver el conflicto entre las partes. Pero deja de tener sentido si dichas partes condicionan su acatamiento al resultado.

Conclusión: Si no van a juicio, pues no hay paradoja. Si van a juicio, tendrán que acatar lo que decida el tribunal y listo.

La mayoría fueron tomadas de: epsilones (Agregar www. al principio y .com al final).

Autor Alberto Rodríguez Santos

Volver al Índice

Home