|
Profe Cossoli |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Acertijos y juegos |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
"Cuanto más juegues, mejor" |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Acertijos variados | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) Un hombre deja una planta de camalote en un estanque el 1 de Junio. Esta planta se reproduce de tal forma que cada día hay el doble que el día anterior. Si el estanque queda totalmente cubierto de camalotes el 30 de Junio, ¿qué día estaría cubierta justamente la mitad del estanque?
2) Dos hombres juegan un partido de tenis al mejor de cinco set. Cuando terminan el partido ambos han ganado tres set. ¿Como puede ser esto?
3) El AVE (tren de Alta Velocidad Española) sale de Madrid con destino a Sevilla a las 13:00 horas. A las 14:15 horas sale un tren de mercancías de Sevilla a Madrid. El AVE lleva una velocidad uniforme de 257 k/h y el tren de mercancías de 102 k/h. Cuando se cruzan, ¿qué tren estará más cerca de Madrid?
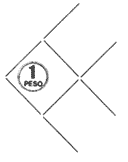
4) Tres amigos entraron a un bar y pidieron unas cervezas por las que el camarero les cobró 30 pesos. Cada uno de los amigos puso 10 pesos y pagaron al pedir. Pero, mientras estaban tomándoselas se dieron cuenta de que había una oferta de 3 cervezas por 25 pesos. Se lo dijeron al camarero y este les devolvió las 5 pesos. Cada uno de los amigos cogió uno de esos pesos y los otros dos se las dejaron de propina al camarero. Por lo tanto cada amigo pagó 9 pesos, por 3 amigos que eran 27 pesos, más los 2 pesos que se quedó el camarero de propina son 29 pesos, ¿dónde está el otro peso? (¡¡9 por 3 + 2=29!!)
5) Juan, Ricardo y Alex, cenan durante tres días una hamburguesa cada uno. Para ello disponen de una plancha en la que caben sólo 2 hamburguesas. Cada lado de la hamburguesa tarda 3 minutos en hacerse. El primer y el segundo día cocinan Juan y Ricardo y ambos invierten 12 minutos en hacer las tres hamburguesas. Ponen dos hamburguesas en la plancha y las hacen por los dos lados, total 6 minutos. Luego ponen la tercera hamburguesa y la hacen por los dos lados, con lo que tardan 6 minutos más. Total 12 minutos. Al tercer día cocina Alex y sólo tarda 9 minutos en hacer las 3 hamburguesas. ¿Cómo puede lograrlo?`
6) Una determinada especie de amebas se reproduce dividiéndose en dos cada día. Entonces, si hoy tenemos una ameba, mañana tendremos dos, pasado mañana cuatro, etc. Cuando comenzamos con una ameba, se tarda 30 días en llenar una cierta superficie con amebas. ¿Cuánto se tarda en cubrir la misma superficie si comenzamos con dos amebas?
7) Mi tío Joaquín tiene que tomar una píldora de cada una de dos medicinas distintas cada día. El farmacéutico le dió un frasco de la medicina A, y un frasco de la medicina B, y dado que ambas píldoras tienen exactamente la misma apariencia, le recomendó que fuera especialmente cuidadoso y no las confundiera. Ayer a la noche puso sobre la mesa una píldora del frasco rotulado "A", y una píldora del frasco rotulado "B", cuando se distrajo por un momento y se dió cuenta que sobre la mesa había tres píldoras. Las píldoras son indistinguibles, pero contando las que quedaban en los frascos mi tío se dió cuenta que por error había dos píldoras del frasco "B", en lugar de una sola como le había recetado el médico. Es extremadamente peligroso tomar más de una píldora por día de cada clase, y las píldoras son muy costosas como para descartarlas y tomar nuevas de los frascos. ¿Cómo hizo mi tío para tomar esa noche, y cada una de las noches siguientes, exactamente una píldora de cada clase?
8) Las fichas de reversi tienen el formato de una ficha del juego de damas, pero tienen una cara blanca y una cara negra. En una mesa hay un número 'x' de fichas de reversi. Solamente 10 de ellas tienen su cara blanca hacia arriba. Nos encontramos ante la mesa con los ojos vendados, y nuestro objetivo es dividir todas las fichas en dos grupos, de modo de que en cada grupo haya el mismo número de fichas con el lado blanco hacia arriba. Obviamente, no se puede mirar las fichas. ¿Cómo se logra el objetivo?
9) Se tienen 10 sacos que contienen 10 monedas de plata cada uno, pero uno de los sacos tiene exclusivamente monedas falsas. Las monedas falsas lucen igual que las genuinas, pero pesan o bien 1 gramo más, o bien 1 gramo menos que las monedas genuinas. Se cuenta con una balanza de un platillo, que permite leer el peso en gramos, y se conoce el peso de las monedas genuinas. ¿Cuál es el mínimo número de pesadas necesarias para determinar cuál es el saco que contiene las monedas falsas?
10) ¿Cuál es el producto de la siguiente serie? (x-a)(x-b)(x-c).......(x-z)
11) SECUENCIA LÓGICA I
¿CUÁL ES EL NÚMERO QUE SIGUE EN ESTA SECUENCIA? 77, 49, 36, .....
12) SECUENCIA II
Serias capaz de decirme que criterio se ha seguido para colocar estos números. 0, 5, 4, 2, 9, 8, 6, 7, 3, 1
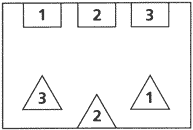
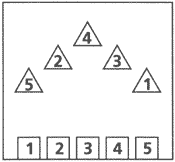
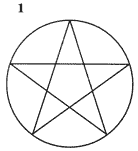
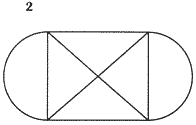
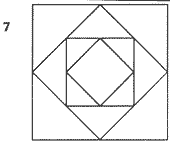
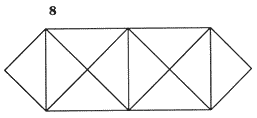
13) SECUENCIA III
Mientras he estado coleccionando acertijos me han aparecido muchos de secuencias lógicas y esta que expongo a continuación es una más.
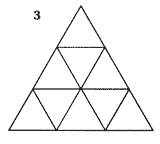
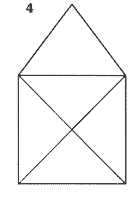
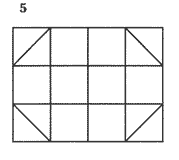
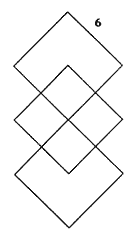
¿QUÉ FIGURA SERÍA LA SIGUIENTE EN LA SECUENCIA ANTERIOR?
14) Un oso camina 10 Km. hacia el sur, 10 hacia el este y 10 hacia el norte, volviendo al punto del que partio. ¿De que color es el oso?
15)En una mesa hay tres sombreros negros y dos blancos. Tres señores en fila india se ponen un sombrero al azar cada uno y sin mirar el color. Se le pregunta al tercero de la fila, que puede ver el color del sombrero del segundo y el primero, si puede decir el color de su sombrero, a lo que responde negativamente. Se le pregunta al segundo que ve solo el sombrero del primero y tampoco puede responder a la pregunta. Por ultimo el primero de la fila que no ve ningún sombrero responde acertadamente de que color es el sombrero que tenia puesto. ¿Cuál es este color y cual es la lógica que uso para saberlo?
16) Un caño que conduce agua se ha roto. Posee un diámetro de 10 cm. Si sustituimos el caño de 10 cm de diámetro por dos caños de 5 cm de diámetro cada uno. ¿ Los dos caños conducirán la misma cantidad de agua?
17) Tenemos doce monedas aparentemente iguales, pero una de ellas tiene un peso ligeramente superior. Usando una balanza de platillos y con solo tres pesadas encontrar la moneda diferente.
18) Un encuestador se dirige a una casa donde es atendido por una mujer: ¿cantidad de hijos? Tres dice ella. ¿edades? El producto de las edades es 36 y la suma es igual al numero de la casa, responde. El encuestador se va pero al rato vuelve y le dice a la mujer que los datos que le dio no son suficientes; la mujer piensa y le dice: tiene razón, la mayor estudia piano. Esto es suficiente para que el encuestador sepa las edades de los hijos. ¿Cuáles son?
19) El alcalde de una cárcel informa que dejara salir de la prisión a una persona al azar para celebrar que hace 25 años que es alcalde. Eligen a un hombre y le dicen que quedara libre si saca de dentro de una caja una bola blanca, habiendo dentro 9 bolas negras y solo 1 blanca. El prisionero se entera por un chivatazo que el alcalde pondrá todas las bolas de color negro, al día siguiente le hace el juego, y el prisionero sale en libertad. ¿Cómo ha conseguido salir de la cárcel si todas las bolas eran negras?
20) Un lechero tiene un cántaro de 8 litros lleno de leche, y dos mas de 5 y de 3 litros. Un cliente le pide exactamente 4 litros. ¿Cómo puede calcular los cuatro litros y dárselos en el cántaro de 5 litros?
21) A un joyero le dan cuatro trozos de cadena de tres eslabones cada uno, y le encargan que los una para hacer con ellos una pulsera. Al hacer el presupuesto de la reparación el joyero calcula que tiene que soldar cuatro eslabones, a un Euro cada uno el precio seria de cuatro Euros, pero el cliente no esta de acuerdo y le dice como hacerlo soldando solo tres eslabones. ¿Cómo lo hizo?
22) Un excursionista es capturado por caníbales y le dicen: Si dices una mentira te matamos lentamente y si dices una verdad te matamos rápidamente. ¿Que dice para que no lo maten?
23) Cuatro gatos cazan cuatro ratones en cuatro minutos. ¿Cuánto tiempo tardan cien gatos en cazar cien ratones?
24) Tres gatos cazan tres ratas en tres minutos. ¿Cuántos gatos hacen falta para atrapar cien ratas en cien minutos?
25) Una rana está en el fondo de un pozo que tiene treinta metros de profundidad. La rana puede dar saltos de una altura de tres metros por la pared, pero como el pozo está resbaladizo luego resbala dos metros hacia abajo. ¿Cuántos saltos necesita para alcanzar el borde del pozo?
26) Un nenúfar (planta acuática) encontrado en una lejana montaña donde viven unos monjes, crece de tal forma que cada día dobla la superficie que ocupa en la extensión de agua donde vive. Se puso uno de ellos en un lago y el nenúfar tardó treinta días en cubrir completamente la superficie del lago. ¿Cuánto tiempo habrían tardado dos nenúfares en cubrir el mismo lago?
27) PENDIENTE EN
EL CAFÉ. Esta mañana se me cayó un pendiente (aro) en el café. Y
aunque la taza estaba llena, el pendiente no se mojó. ¿Por qué?
31) CAMINAR
SOBRE LAS AGUAS. El reverendo Horacio Buenaspalabras anunció que
cierto día, a cierta hora, realizaría un gran milagro: durante
veinte minutos caminaría sobre la superficie del río Hudson sin
hundirse en sus aguas. Una gran muchedumbre se apiñó para presenciar
la hazaña. El reverendo Buenaspalabras realizó exactamente lo que
afirmó que haría. ¿Cómo pudo arreglárselas?
33) Un camión se
queda atascado al cruzar por debajo de un puente. Le sobran apenas
dos centímetros. ¿Se te ocurre algún consejo para darle?
37) Cuando Dios
formó a Adán, ¿dónde le puso la mano?
38) ¿Cómo se
puede llevar agua en un colador?
39) Te caes de
una escalera de 6 metros y aterrizas sobre un camino de cemento,
¡pero no te lastimas! ¿Por qué no?
41) Carolina
vive en el piso diecinueve de un edificio. Cada vez que sube al
ascensor en planta baja, aprieta el botón del cuarto piso, sonde
sale y camina el resto del camino hacia arriba. Cuando deja su
departamento, sin embargo, toma el ascensor todo el trayecto hasta
abajo. Carolina preferiría ir en ascensor antes que caminar, así que
¿por qué hace esto?
45) Al entrar
una noche de mucho viento en un refugio de montaña, se encuentra UD.
con que tiene una sola cerilla y hay, sobre la mesa una vela, y en
la chimenea unos leños. ¿Qué encendería primero?
46) ¿Cómo
pueden permanecer dos personas en pie sobre una hoja de periódico a
un mismo tiempo, sin que puedan tocarse, aunque quisieran?
Naturalmente, no se puede pisar fuera del periódico. 47) Un tonel lleno de vino pesa 35 kg. Cuando está lleno justo hasta la mitad, pesa 19 kg. ¿Cuánto pesa el tonel vacío?
48) La chiflaban las noches. Aquel año recorrió 5.000 kilómetros cambiando regularmente las ruedas, incluida la de repuesto, para que se desgastaran por igual. Al llegar al kilómetro 5.000, ¿durante cuantos kilómetros ha sido utilizada cada rueda?
49) Entrega 4 dados a un amigo tuyo. Le propones que haga una columna con ellos estando tú de espaldas para no ver como los pone y le dices que después de una sola mirada a la columna podrás adivinar la suma de los números que se hallan entre dado y dado y entre primer dado y la mesa (total de 7 caras). ¿Sabes calcularlo?
50) Tener libros en casa no tiene mucho mérito. Lo loable es leerlos. En la estantería de mi casa tengo el Quijote en dos magníficos tomos. El primer tomo tiene 683 páginas y el segundo 539. Una erudita carcoma que los ha visto ha conseguido cavar una galería que va desde la primera página del tomo 1 hasta la última del tomo 2, aparte de las sabrosas tapas. El disgusto ha sido tremendo y he de evaluar los daños para llevarlos a reparar. ¿Me puedes ayudar? Dime cuantas páginas ha perforado la hambrienta carcoma.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Juegos de ingenio | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
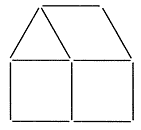
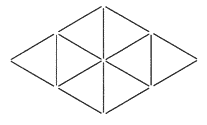
17) COMECOCOS: Hacer tres líneas rectas sobre la m de forma que se consigan 9 triángulos que no se superpongan.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Juegos matemáticos | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1) Escribe en un papel el número 12345679 (ojo, falta el 8) Pide a un amigo que te diga una cifra del 1 al 9.
Multiplícala mentalmente por 9, escribe el resultado bajo el numero 12345679 y pide a tu amigo que multiplique las dos cifras.
Te asombrará el resultado.
2) Pon sobre la mesa un sobre cerrado, un papel y un lapicero. Pide a un amigo que escriba en él papel cualquier número de tres cifras, por ejemplo 528.
Pídele que escriba este mismo numero con las cifras invertidas, en nuestro ejemplo 825 y que reste el menor del mayor, 825-528=297.
Por último que sume los dígitos del numero obtenido, 2+7+9=18.
Entonces abre el sobre y saca un papel que pusiste antes de cerrarlo con la frase "El número obtenido es el 18"
¿Qué como lo sabias?
3) Pon otro sobre encima de la mesa y pide que escriban esta vez un número de 4 dígitos, por ejemplo 2536.
Debajo de ese numero que escriba otro con los mismos dígitos pero en diferente orden, por ejemplo 3265.
Que resten el menor del mayor, 3265-2536=729 y que sumen los dígitos del numero obtenido, 7+2+9=18.
Si el resultado es un numero de dos dígitos que los sumen entre si, 1+8=9.
Abre el sobre y
saca el papel donde escribiste "El numero obtenido es el 9"
4) Piensa en el número de veces a la semana que te gustaria salir a cenar fuera. Multiplícalo por 2 y súmale 5 Multiplícalo por 50
Dependiendo de
tu fecha de cumpleaños: Réstale el año de tu nacimiento incluyendo las 4 cifras.
Obtuviste un
número de 3 cifras:
5) La Cifra perdida
6) Dados revelados
7) ¿Cuál es la diferencia?
8) Multiplicaciones curiosas Pide a un conocido que te diga, en una primera impresión (esto es sin hacer el cálculo), si estas dos multiplicaciones darían el mismo resultado:
Prueba con estas otras dos:
Seguramente la respuesta será un NO. Ahora resuélvele las multiplicaciones. Curiosos los resultados ¿no?
SUGERENCIA Puedes probar con otros números siguiendo el esquema:
Los juegos y acertijos fueron tomados de: ar.geocities.com/elportaldewebo (Agregar http:// al comienzo) chelis.iespana.es (Agregar http:// al comienzo) enplenitud.com (Agregar www. al comienzo) juegosdelogica.com/neuronas (Agregar www. al comienzo) matematicas.net/paraíso (Agregar www. al comienzo) mlevitus.com (Agregar www. al comienzo) usuarios.lycos.es/acertijolandia (Agregar http:// al comienzo)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||