|
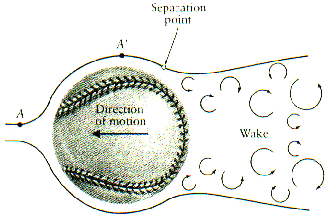
��� The fastball is maybe the most important pitch in baseball.� Most pitchers use the fastball as their number one pitch, and use other pitches to complement the fastball.� A fastball is simply that, a pitch that travels straight toward the batter, as fast as possible.� Some of the greatest pitchers in the game have been primarily fastball pitchers.� In 1914, Walter Johnson threw a baseball determined to have a velocity of 99.7 mph.� More recently, Nolan Ryan was clocked at 100.7 mph.� These speeds of the baseball are as clocked as it crosses the plate.� A baseball loses about 8 mph between the pitchers hand and home plate.� So coming out of Nolan Ryan's hand, the ball was actually traveling with a velocity of about 109 mph.� This speed (8 mph) is bled off because of the fluid that the baseball must travel through on its way to the batter.� The fluid in this case is air.� Air is a fluid that possesses viscosity.� As shown in the figure below, the fluid (air) particles do not travel all the way around the ball.� At some point beyond A', a separation point exists where the air stops travelling around the ball.� It is hear that a backflow develops.� This causes a chaotic, swirling flow, called the wake, around the rear of the baseball.� Because of this, the pressuer in the wake region is much lower than the pressure at the front of the ball.� This creates a drag force.�� For a fastball, there is not horizontal spin, so the drag force is symmetrical.� It simple slows the ball down, without causing any deviation of path.� This is the reason that a fastball may lose up to 8 mph between the pitcher and the batter.� |
|
|
��� A pitch known as the rising fastball is basically a fastball with backspin.� The legendary Walter Johnson was reported to be able to throw a fastball that actually defied gravity and rose as it approached the plate.� The reason it might rise is the same reason a regular fastball slows down as previously discussed.� A pitch with backspin would create lower pressure above the ball, causing it to rise.� This pressure would have to be greater than the force of gravity on the ball, mass * gravity.� Assuming a ball weighs .32 pounds, and assuming a ball is thrown at 147 feet per second (100 mph), we can use the equation F= 6.4 x 10^-7 wv to calculate the required backspin to overcome the force of gravity on the ball and actually allow the ball to rise.� Solving for w gives an rpm of 3400.� The best college pitchers throw about 2300 rpm.� So, right now, it is highly unlikely that anybody can throw a fastball with enough rpm to get it to actually rise.� It is also unlikely that Walter Johnson's fastball rose.� Most likely, it just didn't drop as much as most people's fastball, so it gave the illusion of rising.� |
|