Work-Energy
Theorem
Back
to Physics World
Back to Special Relativity
The
work done on a particle under the force F in moving it from r1
to r2
is defined as
![]()
Let
us now replace the v in terms of p to help the integration and
make it easier. The momentum is given by p = mv = gm0v
Þ v = p/gm0v.
Substituting this expression into Eq. (1) gives
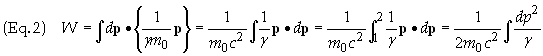
where
![]() . Eq. (2) can now be expressed as
. Eq. (2) can now be expressed as
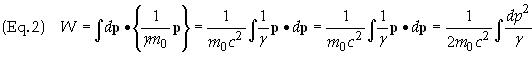
Integrate by parts using the template
![]()
Let u
= g-1
dv = dp2
du
= - g-2dg
v = p2
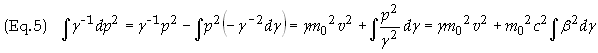
From the
definition of g we obtain
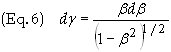
Substituting
into Eq. (5) we obtain
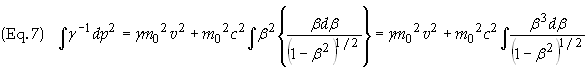
The
last integral on the right side can be shown to be
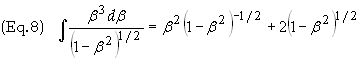
Differentiating
both sides verifies this fact. Eq. (7) can now be expressed as
![]()
Substituting
this back into Eq. (4) gives, omitting limits of integration for the moment
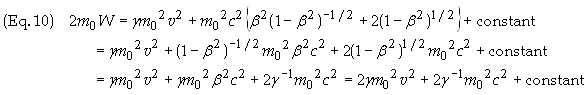
Solving
for W gives
![]()
Choose
the constant of integration such that the kinetic energy K = 0 when
W = 0. This gives a constant of E0
= m0c2,
i.e. objects rest energy. The kinetic energy is therefore given by
![]()
where E
= mc2.
Therefore the Eq. (1) becomes
![]()
This
can be expressed as
![]()
If
the force can be expressed as
![]()
where
the second term on the right side of Eq. (15) is defined such that
![]()
Substituting
Eq. (13) into Eq. (1) gives
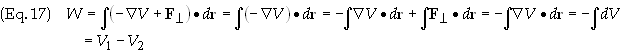
Equating
with Eq. (13) we obtain
![]()
which
can be written as
![]()
If we
now add on the rest energy E0
= m0c2,
which is a
constant during the motion of the particle, to each side we get
the total energy which we’ll label T. Note that E = K + E0
= inertial energy so that we can express Eq. (19) as
![]()