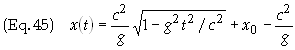Uniform Acceleration
Back
to Physics World
Back to Special Relativity
The
purpose of this page is to derive the equations of motion for a particle that is
accelerating uniformly with respect to an inertial frame of reference. Uniform
acceleration is defined as motion for which the acceleration of the particle
as measured in a commoving frame always has the same constant value. We seek to
derive
(i) Position and as a function of proper time i.e. x = x(t), and t = t(t).
(ii)
Position as a function
of time, i.e. x = x(t).
Position and Time as a
Function of Proper Time
The
4-velocity of a particle is defined as
![]()
Since
the magnitude of U is invariant we may determine its value as measured in
the momentarily commoving reference frame (MCRF) to. In the MCRF g
= 1, so that
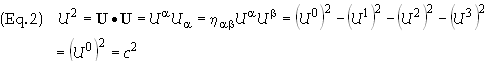
![]()
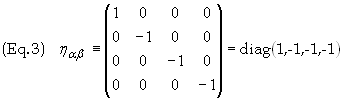
The
particle’s 4-acceleration is defined as
![]()
In
Minkowski coordinates the components are
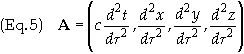
Taking
the derivative of Eq. (2) with respect to proper time gives
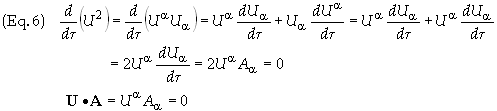
This
states that 4-velocity of a particle is always orthogonal to its 4-acceleration.
“Uniform acceleration” means that the acceleration as measured in the
MCRF has a constant value g, ie.
![]()
Assume
the particle is accelerating uniformly in the +x direction. Then
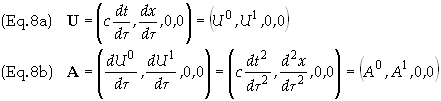
Eq. (2),
(6), (7) and (8) form the system of equations
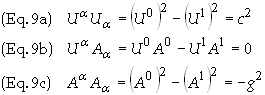
Solve
Eq. (9b) for A1
to obtain A1
= (U0/U1)
A0.
Substituting this expression into Eq. (9c) yields
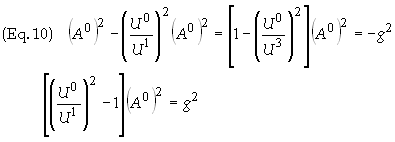
The term
on the left side of the last expression in Eq. (10) can be simplified by
utilizing Eq. (9a). Divide Eq. (9a) by U1
yields
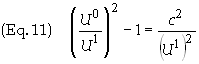
Substitution
into Eq. (10) gives us
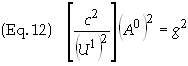
We now
simply solve for A0
to obtain
![]()
To
obtain a similar relation for A1
we use a similar procedure. Solve Eq. (9b) for A0
to obtain A0
= (U1/U0)
A1.
Substituting this expression into Eq. (9c) yields
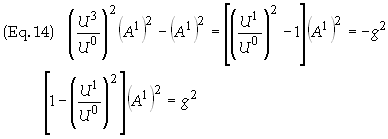
Once
again, the term on the left side of the last expression in Eq. (13) can be
simplified by utilizing Eq. (9a). Divide Eq. (9a) by U0
yields
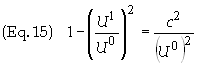
Substitution
into Eq. (13) gives, after simplification
![]()
Eq. (12)
and Eq. (15) together form a coupled system of differential equations
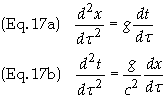
To
uncouple these equations differentiate Eq. (176a) with respect to proper time
and substitute in Eq. (17b) to obtain
![]()
Differentiate
Eq. (16b) with respect to proper time and substitute in Eq. (16a) to obtain
![]()
Eq. (18)
has the general solution
![]()
where l
= g/c. The initial conditions are

The
derivatives are with respect to proper time and have the value
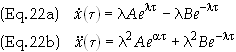
The
initial conditions are then
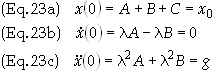
The
solution to this set of equations is
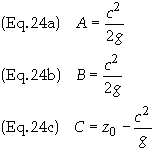
The
solution to Eq. (17a) is therefore
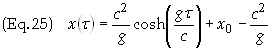
Eq. (19)
has the general solution
![]()
The
derivatives have the value
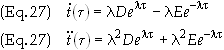
The
initial conditions are
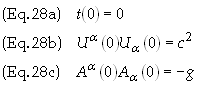
Substituting
the values from Eq. (21) into Eq. (28) gives the initial values of t.
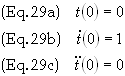
The
initial conditions are then
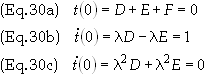
The
solution to this set of equations is
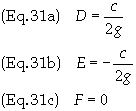
The
solution to Eq. (17b) is therefore
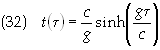
If we
define
![]()
then the
parametric equations of motion become
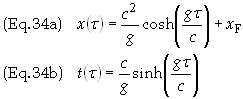
Subtract
xF
from Eq. (34a) and multiply Eq. (34a) and Eq. (34b) through by a º
g/c2 to
obtain
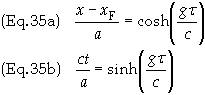
Square
Eq. (35a) and Eq. (35b) and subtract the former from the later using the
identity
![]()
to
obtain
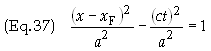
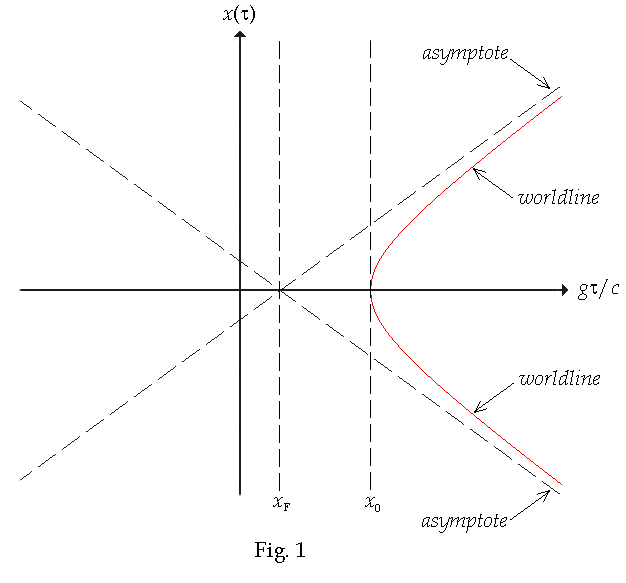
Eq. (37)
is the equation for a hyperbola, which crosses the x-axis at x0
and for which the asymptotes cross at xF.
The point at which the asymptotes cross is referred to as the focal point,
hence he “F” subscript. The motion is therefore hyperbolic, i.e. the curve
in a spacetime diagram is an hyperboloid as shown below in Fig. 1
Position
as a Function of Time
There
are two ways to defined uniform acceleration; one mentioned above, the other is
that of constant force. Since the force transforms as
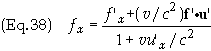
it
follows that in the MCRF where u’ = 0 (and hence u’x
= 0)
![]()
In the
MCRF f’x
= m0a’x.
Since the particle is at rest in the moving frame ux
= v.
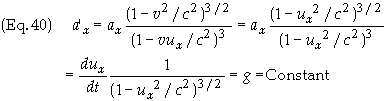
Eq. (40)
may be written as
![]()
Integrating
this expression
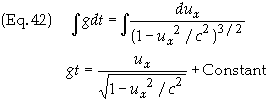
The
constant of integration is chosen such that v(0) = 0. I.e. Constant = 0.
Solving for ux
gives
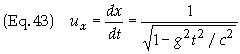
Integrating
Eq. (43) gives
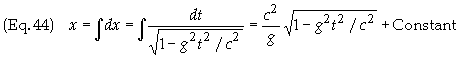
Once
again we find the constant of integration by apply the initial condition x(0)
= x0. This gives the final result