Longitudinal and Transverse Mass 

Back to Physics World
Back to Special Relativity

The force on a relativistic particle is given by

m º gm₀ is the mass of the particle where m₀ is the rest mass is. The particle’s mass is related to particle’s kinetic energy, K, by

If the particle’s rest m0 is constant then differentiating Eq. (2) with respect to time gives

According to the work-energy theorem the time rate of change of the particle’s kinetic energy is dot product of force and velocity, i.e.

Therefore the time rate of change of the particle’s mass is given by

Substituting into Eq. (1) yields

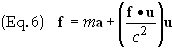
Eq. (6) shows that the force, acceleration and velocity vectors are co-planar. See Figure 1 below

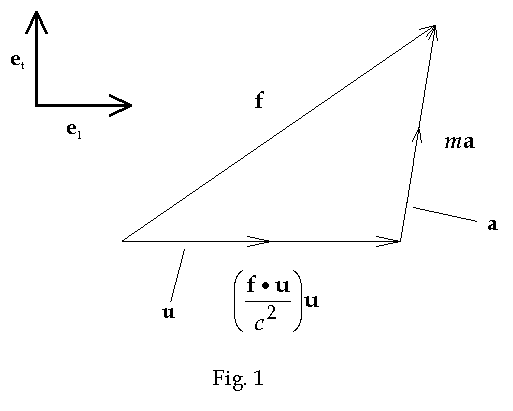
The force and acceleration may therefore be resolved into components parallel and transverse to the direction of motion, i.e. into components parallel and transverse to u. The transverse component will lie in the plane of the three vectors as shown in Fig. 1. In terms of unit vectors parallel and transverse to u = uel as shown in Fig. 1, the force and acceleration become

Substitute Eq. (7) and (8) into Eq. (6) to obtain

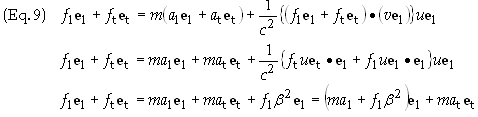
Since e_l and e_t are linearly independent we can equate the components. We directly obtain the transverse component as

Equate the longitudinal component and solve for the transverse force

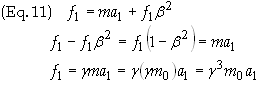
 Summary

where

The force may now be expressed as

Back to Special Relativity
Back to Physics World