Conservation Laws
Back
to Physics World
Back to Special Relativity
The angular
momentum density tensor is defined as
Mabs
is conserved with respect to the a
index, i.e.
when the
system is conservative, i.e.
then Eq.
(2) can be demonstrated by taking the partial derivative of Eq. (1) with respect
to xa
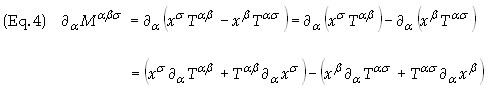
Recall
that
. Since Tsb
= Tbs,
it follows from Eq. (2) that
And thus
Eq. (2) is confirmed. The condition given in Eq. (2) yields two conservation
laws (1) conservation of angular momentum and (2) conservation of linear
momentum which gives six integrals of motion. These laws are demonstrated by
considering the angular momentum tensor defined as
where dV is a volume element. The condition of constancy arises from Eq. (2). The notation will be more obvious if we introduce the following three vectors
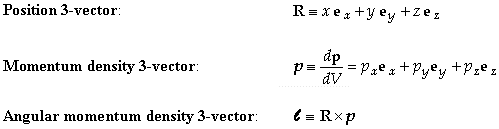
The angular momentum 3-vector is then
Substituting
T0k
= pkc
and
xa
º
(ct,
x, y, z) we get
Recalling the definition of Lij we find
Therefore
our first three constants of motion are
Lx
, Ly
, and
Lz
,
Our next
set of conserved quantities is
Substituting
x0
º
ct,
T0k
= pkc
and T00 =
rc2
into Eq. (11) gives
The
total momentum of the system is constant and is defined as
The
total mass of the system is constant and defined as
The
quantity
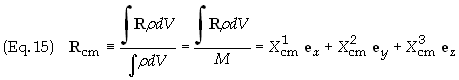
is
defined as the center of mass vector of the system. Substituting the
components of the center of mass vector into Eq. (12) gives
Differentiating
Eq. (16) with respect to times gives
In
vector notation Eq. (17) takes the form
Therefore,
according to Eq. (19), the total momentum of the system is the total mass of the
system times the velocity of the center of mass. The center of energy is defined
as
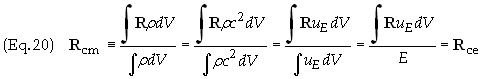
The
E in Eq. (19) is the total inertial energy of the system.
Since energy density is proportion to mass density, i.e. uE =
rc2,
which implies the following relationship
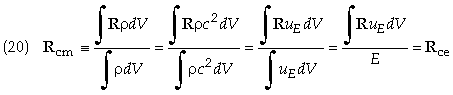
Thus the
center of mass vector is equal to the center of energy vector.