Step Potentials

The transmission and reflection coefficients are defined in terms of the probability current, J, also known as current density

Consider a one-dimensional a beam of particles that are plane wave states. The beam is moves in x-direction and impinges on a barrier as shown in Fig. 1 below 

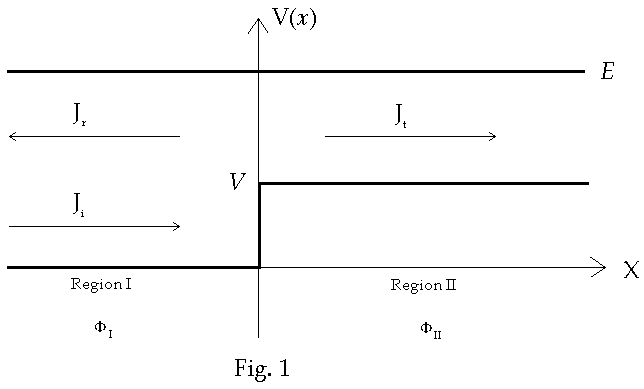
The transmission coefficient T and reflection coefficient R are defined in terms of the components of the probability current. Let J_i represent the incoming current, J_t represent the incoming transmitted current, and Let J_r represent the reflected current

General Case of Step Potential for E > V

 The magnitude of the momentum of the particles in the incoming, transmitted and reflected beams are, respectively

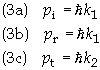
where, in general, k₁ � k₂. The potential is constant for x < 0 and for x > 0 so the wavefunction in each domain is that of a free particle. Since energy is conserved it follows that E_i = E_t = E_r . The wavefunction for the incoming, transmitted and reflected beams are, respectively

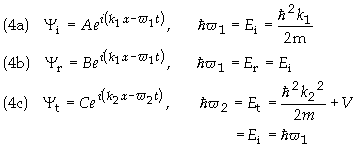
Using Eq. (4a) in the relation for the current in Eq. (1) gives the x-component of the current density

 Substituting Eq. (4a) into Eq. (5)

 A similarly procedure for the transmitted and reflected current densities

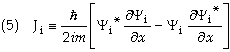
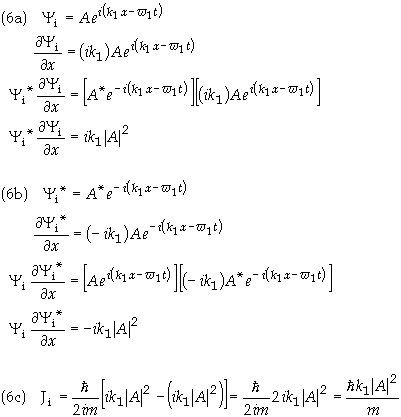
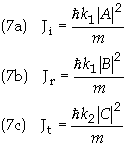
We these values for the currents the transmission and reflection coefficients become

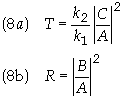
The time-independent Schrodinger equation is

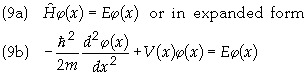
For the step potential shown in Fig. 1 can broken up into two domains. Region I is the domain x < 0 and Region II is the domain x > 0.  The wavefunction will be partitioned into two parts as well corresponding to each domain. In Region I the Hamiltonian consists entirely of the kinetic energy term so Eq. (9b) reduces to 

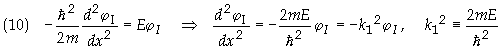
In Region II the Hamiltonian has a kinetic energy term plus a constant potential 

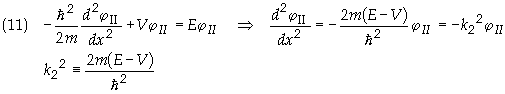
The solution to Eq. (9) and (10) is

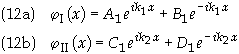
Since the time-independent Schrodinger equation is second order there must be two boundary conditions. First note that we can set since it is the coefficient of a wave coming from +infinity and since there is no such wave we can set D = 0. They are determined by the condition that the wavefunction and its first derivative must be continuous. Applying this criteria at x = 0 means

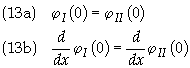
Taking the derivative of Eq. (12) gives

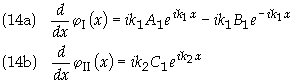
Applying the boundary condition in Eq. (13a) gives

Appling the boundary condition in Eq. (12b) gives

Eqs. (15) and (16) can be written simply as 

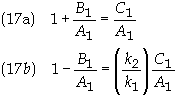
Eq. (17) can be solved for the ratios B₁/A₁ and C₁/A₁ to give

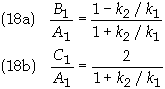
The transmission coefficient can now be written as 

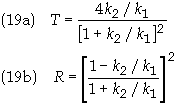
General Case of Step Potential for E < V  

In Region I we have the same situation as above and therefore the same solution as in Eq. (12a). The relationship for the reflection coefficient will therefore have the same relation as above, i.e. R will still be given as in Eq. (8b).   However in Region II the quantity E – V is negative. Therefore

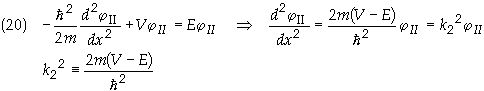
There are two solutions to Eq. (20), one of which is an exponentially increasing function. This must be discarded since it leads to a diverging probability density. Therefore the solution is

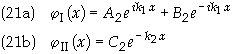
The derivatives are

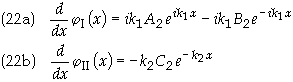
Just as above, applying the boundary condition defined in Eq. (13a) gives

Applying the boundary condition defined in Eq. (13b) gives

Eqs. (23) and (24) can be written simply as

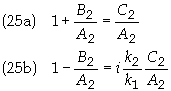
Eq. (25) can be solved for the ratios B₂/A₂ and C₂/A₂ to give 

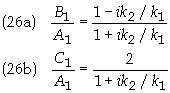
Since the right side of Eq. (26) is of the form z*/z and therefore | z*/z| = 1. This gives

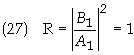
The transmission coefficient is found by using the relation R + T = 1. It follows that T = 0. This means that the transmitted current density is zero. The wavefunction in Region II is multiplied by a decreasing exponential. The wavefunction therefore does not represent a propagating wave. Such a wave is called an evanescent wave.

Rectangular Barrier and Tunneling: Case E > V 

Consider now a rectangular barrier for which E > V as shown in Fig. 2  

 Just as above, in each region the potential is constant. The solutions are again similar to that in E. (4) above. We have

 Conservation of energy implies

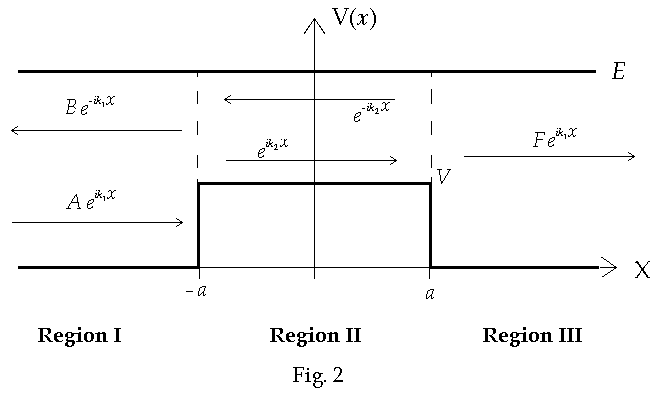
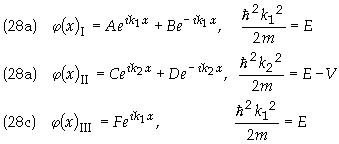
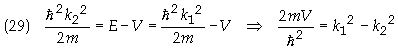
The boundary conditions are

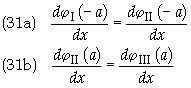
Applying the boundary conditions in Eq. (30) gives

 To apply the boundary condition in Eq. (31) we need to first take the derivative of each term in Eq. (30)

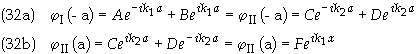
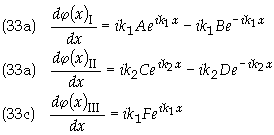
Applying the boundary conditions in Eq. (31) gives

 Dividing Eq. (32) by A gives

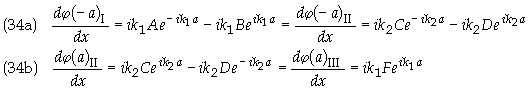
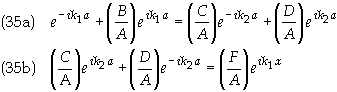
Dividing Eq. (34) by A gives

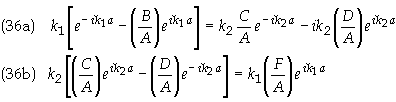
Summary of results

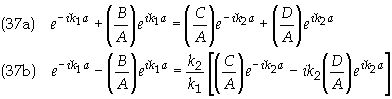
After some tedious algebra these equations can be put into the form

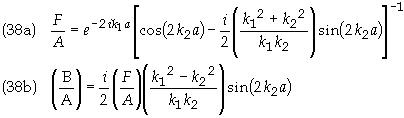
From a calculation similar to Eq. (7) it can be shown that the transmission and reflection currents are

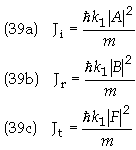
Therefore the transmission and reflection currents are, respectively

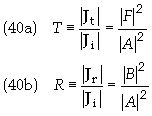
Substituting Eq. (38a) into 1/T gives, using the values or the energy in Eq. (28)

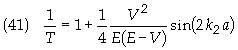
To find R use the relation  T + R = 1 to give R = 1 – T.