Physics
World
Back to Quantum Mechanics
The
quantum state of a particle is defined, at any given place r, at any
given moment t, by a wave function Y(r,
t). The probabilistic interpretation of the wave function states that the
probability of finding the particle located within a volume dr3
located at r is
where
it is assumed that Y(r,t) has been normalized. The total
probability of finding the particle somewhere is 1, which demands
Any
function Y(r,
t)
for which the integral in Eq. (2) converges is said to be square-integrable.
The set of square-integrable functions is called L2.
Since waves function represent physical properties of a system there are
additional requirements placed on Y(r,
t).
For example; Y(r,
t)
must be defined everywhere, continuous and infinitely differentiable. This space
Á
is defined as the set of wave functions that are sufficiently regular functions
of L2.
Therefore Y(r,
t)
belongs to a subspace of L2.
Á-space is called wave function space.
Er
– State Space
There
are various ways of representing or representing a quantum state. For example;
Instead of a wave function Y(r,
t)
that depends on the particle’s position at time t we could just as well use a
wave function that depends on the particles momentum p at time t,
i.e. F(p,
t).
This is much like the case in classical mechanics where a vector can be
expressed in various ways using different basis vectors. The fundamental object
being the vector. So too in the case of quantum mechanics where the fundamental
object is the quantum state. Thus each quantum state is characterized by a state
vector belonging to an abstract space Er
called
the state space of a particle. Not all physical systems can be
represented by a wave function. The introduction of state space and space
vectors generalizes the formalism to allow these systems to have a
representation. The symbol E will be used to represent a general state
space.
- “Ket” vectorAny
element of a state space E is called a ket vector, or
simply, a ket. A ket is represented by ”
“ with a symbol which distinguishes it from all other kets in E, i.e.
. We can now associate every square-integrable function in Á
with a ket in Er,
i.e.
- Scalar Product
To each
pair of kets,
and
, we associate a complex number which is called the scalar product,
denoted
, and defined, for three dimensions, as
The
scalar product has the following properties {Note: C* represents the complex
conjugate of C}
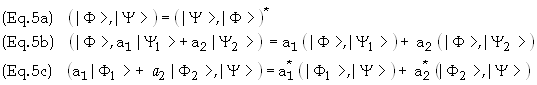
A linear
functional c
is a linear function which associates a complex number, a,
with every ket,
or a =
c(
). i.e. for
Î
E and a
Î C = Set of complex numbers,
The set
of linear functionals defined on the kets
Î
E defines a vector space, is called the dual space of E and
denoted E*.
The elements of E* are,
of course, vectors themselves.
- “Bra”
vector
An element of E*
is called a bra vector, r simply, bra. Similar to the ket notation
a bra is represented by ”
“ with a symbol which distinguishes it from all other bras in E*,
i.e.
Î
E*.
For example: The bra
represents the functional c.
The notation c(
) may thus be replaced with
, i.e.
Briefly, Eq. (6) states that the functional
maps the ket
to a complex number that is denoted
.
To every ket there is a bra. The ket
provides a definition of a linear
functional which associates each ket
the complex number
. Let
be
the functional, which maps
to
. I.e.
Therefore for every ket
there is a bra
. However the converse is not true.
Therefore the bra – ket association for a linear sum is
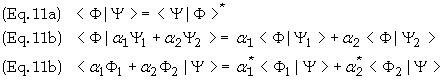
H
- Hilbert Space
A Hilbert space H
is an inner product space that is complete with respect to the norm defined
by the inner product. A Hilbert space has the following properties:
(i) The space is linear: If a1
and a2
are two arbitrary constants and F1, F2 Î
of H
then Y = a1F1 + a2F2 Î H
(ii) There
is a scalar product: For any two elements F and Y there
is a scalar product defined on H.
The inner product of F and Y is
denoted
.
(iii) Each
element has a norm: The norm of each element is related to the scalar
product by
(iv) H
is complete; Every Cauchy sequence of functions in H
converges to an element in H.
A Cauchy sequence {Fn}
is defined such that
