Gaussian
State
Physics
World
Back to Quantum Mechanics
Consider
the one-dimensional problem where a particle is known to be in the state
![]()
The
lengths x0
and a are constants, p0 is
a constant which represents the momentum of the particle and w0
is an angular frequency. A is a constant selected such that the state is
normalized so that the |y|2
represents a probability density, i.e. P(x) = |y|2
. The normalization condition
is
![]()
where
![]()
The
integral in Eq. (2) then becomes
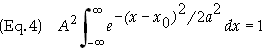
Make the
following substitution:
![]() dx =
adh
dx =
adh
![]()
The
integral has the value
![]()
Therefore
![]()
The
expectation of x, i.e. <x>, can now be evaluated. By
definition
![]()
Substituting
the value of Y
from Eq. (1) gives
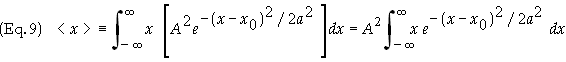
![]() , where
, where
![]() , dx =
adh
, dx =
adh
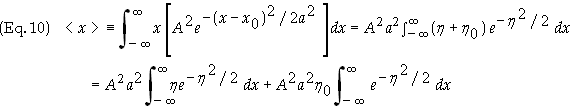
The
first term on the right hand side is an integral over symmetric limits of an odd
function and thus integrates to zero. The
second term on the right is readily evaluated from Eqs. (6)
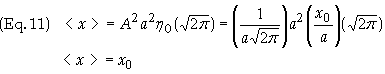
The
probability density P(x) = |Y(x)|2
in the case of the wave function defined in Eq. (1), is given by
![]()
is know
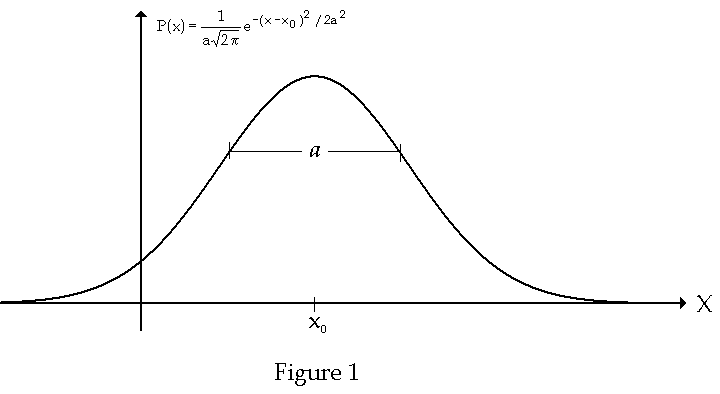
as a Gaussian or normal distribution. a2
is call the variance of x. As shown in the diagram below, a
and, thus a2,
is a measure of the spread of P(x).
The
expectation of the x-component of the momentum, <px>
can now be evaluated. Using the operator defined by
![]()
![]()
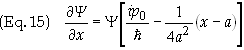
![]()
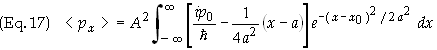
![]()
The
integral in Eq. (18) consists of two terms. The second term on the right
vanishes since its integral an integral of an odd function over symmetric
limits. Only the first term does not vanish
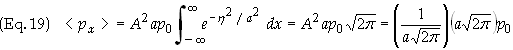
Therefore
![]()