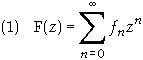
Function of an Operator

Physics World

Consider the power series expansion of a arbitrary analytic function F

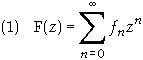
The power series is assumed to converge within a given domain of the argument, i.e. the function is assumed to be analytic on a finite interval. The definition of a function of an operator F is given in terms on the coefficients, f_n. That is to say that the function, F, of an operator, , is defined as

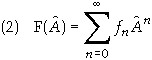
This series will have an interval of convergence that will depend on the eigenvalues of . Note that if F(z) is a real function then all f_n are real. Also readily seen from Eq. (2) is that if is an Hermitian operator then F() is also an Hermitian operator. As an example consider the function e^z. This function can be expressed as a power series by using the MacClaurin series defined as

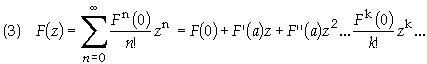
For the present case of e^z is rather simple since the coefficients are readily found since Fⁿ (z) = e^z so Fⁿ (0) =1. The series becomes

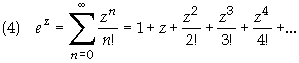
To find the function of the operator simply put in the operator where z belongs. I.e.

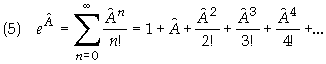
As another example we’ll use F(z) = z^1/2. That is to say we want to find the square root of the operator. However this time we can’t use a MacClaurin series since Fⁿ (0) is undefined. We therefore turn to the Taylor series

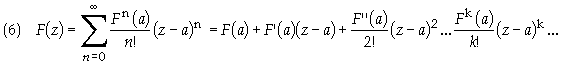
a is an arbitrary number and as such we are free to choose it in any way we see fit so we choose it so that he power series is the simplest. With this choice the Taylor series is

The square root of an operator is then

As a concrete example consider the following operator

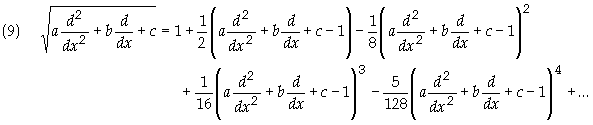
Let  be an eigenvector of the linear operator  with eigenvalue value a. Then

If  is applied n times then we will get

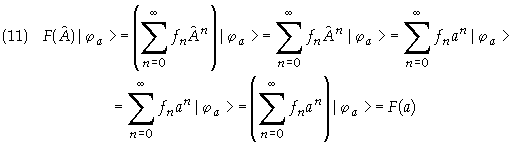
If we wish to find the eigenvalues of  then we substitute the power series expansion of the operator function as given in Eq. (2) and then simplify

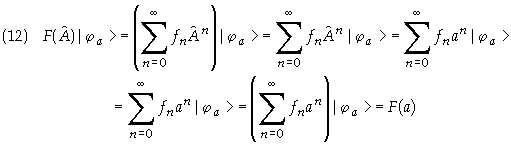
This demonstrates that the following: If is an eigenvector of  with the eigenvalue a. then is also an eigenvector of F() with the eigenvalue F(a).

Let   be an eigenket of the Hamiltonian. Then

Now we wish to find the eigenvalues, Q_n of the operator where

This is in the form of Eq. (5) if we set

Substituting the Eq. (15) into Eq. (5) we get

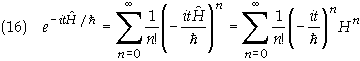
Multiplying Eq. (16) with from the right gives

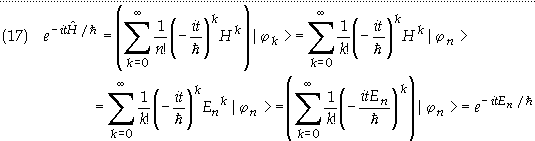
Therefore the eigenvalues of  are

 Physics World