Moment of Inertia Tensor

Back to Physics World
Back to Classical Mechanics

The angular momentum L of a point particle of momentum p = mv located at r is defined as

This relation is defined relative to the origin of the coordinate system. Given another coordinate system there will be another value of the particle’s angular momentum. The angular velocity w of the particle is related to the particle’s v velocity and position r as

L may be now expressed in terms of w as 

For a system of point particles the total angular momentum is defined as 

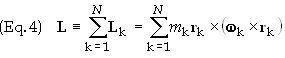
For a rigid body having a continuous mass distribution of mass density r the mass of an infinitesimal element of the body is given by dm = r dV. The angular momentum of this element is then

The total angular momentum of a rigid body is then found to be

Evaluate this in Cartesian coordinates. Let e1, e2, and e3 be unit vectors in the direction of the x, y, and z-axes respectively. In terms of these basis vectors 

The vector under the integral sign in Eq. (6) now becomes

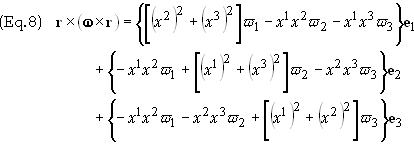
Substituting into Eq. (6) we obtain

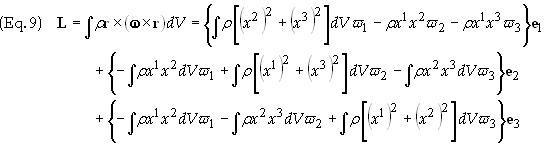
Define the matrix moment of inertia tensor, I, whose components I_jk = I_kj may be arranged in matrix form as

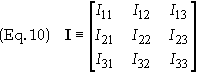
where 

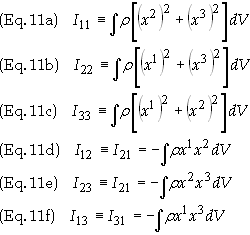
The total angular momentum may now be expressed entirely in terms of w and I as 

This can be simplified to 

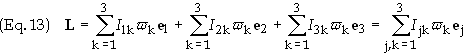
Kinetic Energy

An expression for the kinetic energy of a rigid body rotating at constant angular momentum can be given in terms of the inertia tensor defined about in Eq. (11). The total kinetic energy of such a body is defined as 

The term w´r is given in Eq. (7) above. The magnitude squared of this quantity has the value 

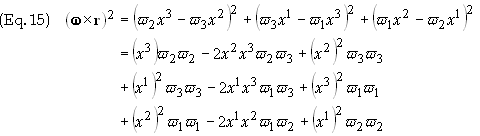
Rearranging terms gives 

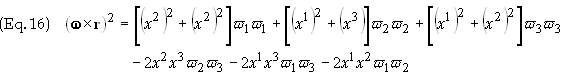
Substitute this result into Eq. (14) to obtain 

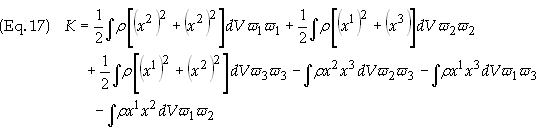
Substituting the components of the moment of inertia tensor, defined in Eq. (11) 

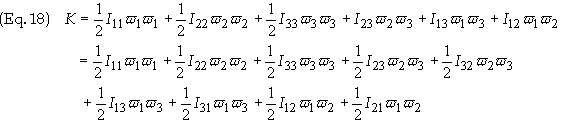
Substituting the double summation symbol so as to simplify Eq. (18) gives 

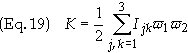
Back to Classical Mechanics
Back to Physics World