Geometric Equation of Motion  

Back to Physics World
Back to Classical Mechanics

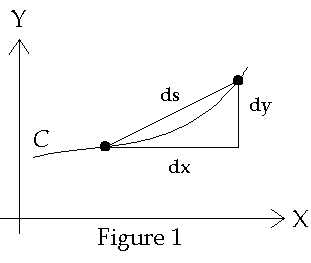
The equation of motion can be derived from Lagrange’s equations. When expressed in geometric terms using the metric tensor the classical equation of motion for zero force motion has the form of the geodesic equation.  In Euclidean geometry the infinitesimal distance, ds, between two closely spaced points is shown in Fig. 1 below 

given in terms of the metric tensor for flat space h_ij = diag(1, 1, 1) as 

Einstein’s convention is employed here; when an index appears twice in a term, once as a superscript and once as a subscript, the summation is implied over the valid range of the index, in this case the range is from 1 to 3. The metric tensor satisfies the following relations 

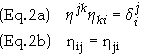
From herein we will use generalized coordinates qⁱ in which the components of the metric tenors will be labeled as g_ij. Dividing Eq. (1) through by dt2 gives the square of the velocity, i.e. 

The kinetic energy, T, is then given by 

The Lagrangian is then given by 

It is here assumed that V is only a function of position, and not velocity dependant, and therefore does not depend on time explicitly. The equations of motion may be obtained through the use of Lagrange’s equations 

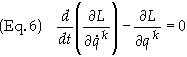
The first step to finding the equation of motion is to calculate the following quantity, noting that the components of the metric tensor are not functions of the velocity 

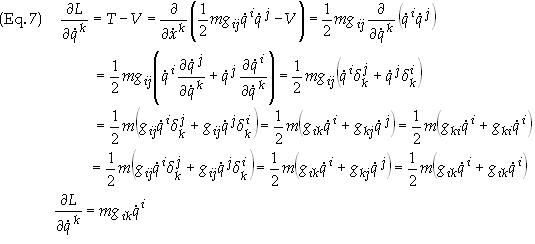
The next step is to take the derivative of this result with respect to time 

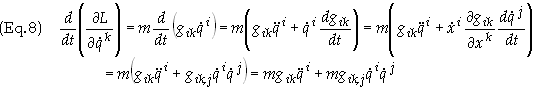
The next step is to find the right hand side of Eq. (6) by taking the partial derivative of Eq. (5) 

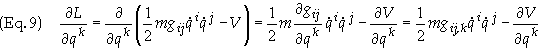
Equating Eq. (9) with Eq. (10) we obtain 

This result can be simplified with some index gymnastics, i.e. note that the second term on the left hand side can be rewritten as 

Substituting into Eq. (10) gives upon rearrangement of terms 

Multiply through by g_nk to get 

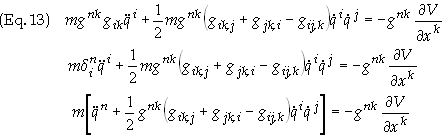
Eq. (13) may also be simplified considerably. Recall the definition of the Christoffel symbols 

The covariant components, F_k, of the force are defined as  

The contravariant, F_k, components of the force are defined as  

Eq. (13) may now be expressed in a simplified form as 

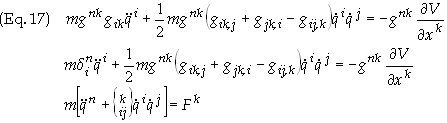
This too may be simplified by employing the absolute derivative of the components of a vector which are defined as 

Back to Classical Mechanics
Back to Physics World