Basic Theorems for Mechanics

Back to Physics World
Back to Mechanics

Definitions of Basic Terms

r is the position vector. This is a vector is defined such that the tail end is collocated at a point referred to as the origin and the other end, i.e. the arrow, is at the point of interest.

v º dr/dt is defined as the velocity vector of a particle.

There is a quantity m such that for all particles in an inertial frame mv is conserved in all elastic collisions. m is called the mass of the particle.

p º mv is defined as the momentum vector of the particle.

F º dp/dt is defined as the force vector. This is sometimes referred to as Newton’s Second Law.

L º r ´ p is defined as the angular momentum vector of the particle.

N º r ´ p defined as the torque vector of the particle.

Torque and Angular Momentum

To find the relationship between L and N we take the time derivative of L

The second expression on the right hand side in the last equality vanishes since v is parallel to mv and thus the cross product vanishes. We therefore arrive at

Therefore the torque is the time rate of change of angular momentum.

Conservation of Angular momentum: When the torque on a particle is zero then the angular momentum is a constant in time.

Work-Energy Theorem

Consider the work done on a non-relativistic particle moving a particle from point 1 to point 2. This work is defined as

K is defined as the kinetic energy of the particle and has the value . Therefore the work done on a particle moving it from point 1 to point 2 changes the kinetic energy as described in Eq. (4).

Work and Change in Potential Energy 

If F is a conservative for such that  then according to a well-known theorem of vector analysis, a necessary and sufficient condition, that work is independent of path and the force will be the gradient of some function, i.e.

Total Mechanical Energy of a Particle

Comparing Eq. (5) with Eq. (8) we find

Upon rearranging terms in Eq. (9) we obtain

Thus we have the conservation of Total Mechanical Energy of a particle: If the forces acting on the system are conservative then the total mechanical energy = E = K + V, is conserved, i.e. constant in time.

Mechanics of a system of particles

We now generalize from a system of one particle to an arbitrary system with multiple particles. The force on a particle in the system consists of two types. The external force acting on particle i is then expressed as Fi (e). The force of the ith internal particle with the jth internal particle is expressed as Fji. With this in mind we can express Newton’s second law for the ith particle

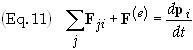
We now assume that the forces F_ji and F_i ^(e) obey the Newton’s third law  - The forces pairs F_ji + F_ij must cancel each other out due to Newton’s third law, although they do not have to be directed along the same line.

This is a statement of Newton’s third law and is referred to as the weak form of the third law. We can now sum all the particles in the above equation to obtain

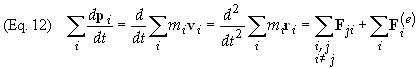
Our next observation is that the total external force is given by

We must divert our attention to the center of mass since it plays a large role in conservation theorems. The center of mass vector, R [1] for a system of particles, defined by

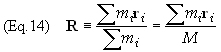
With this definition of R it is readily seen that

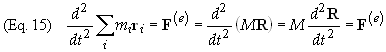
From this we see that the center of mass of a system of particles moves as if the total external force were acting on the entire mass of the system concentrated at the center of mass. Taking the derivative of Eq. (15) we obtain 

I.e. the total linear momentum of the system, which equals the total mass of the system, times the velocity of the center of mass.

From Eq. (15) and Eq. (16) the following is deduced. 

Conservation Theorem for Linear Momentum of a System of Particles: If the total external force is zero then the total linear momentum of the system is conserved.

 To find the total torque on a system of particles we start with Eq. (11) and take the cross product with it and ri and take the summation over i obtain 

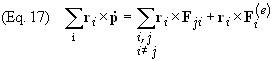
From Eq. (1) we see that we can write 

The first term on the right hand side vanishes leaving only the second term since the first term vanishes since v is parallel to mv. This leaves us with 

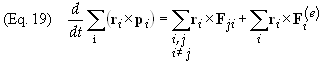
If we assume the weak law of action reaction then first term on the right side of in Eq. (11) vanishes since this is a sum of pairs of which vanish since the sum is of terms such as 

 The notation and r_ij can be seen in Fig. 1 below

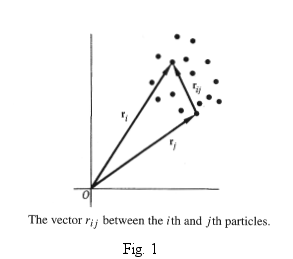
If the forces between particles all satisfy the strong form of action reaction then the force will be parallel to the line connecting the particles and therefore parallel to rij and thus all the cross products rij´F will vanish. This leaves Eq. (13) in the form

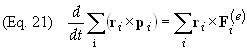
The left side we recognize as the derivative of the total angular momentum and the right side we recognize as the total external torque on the system, or in symbols

Conservation Theorem for Angular Momentum of a System of Particles: If the total external force is zero then the total angular momentum of the system is conserved.

[1] Not to be confused with the center of mass frame. The center of mass vector is a vector where the center of mass frame is a frame of reference.

Back to Mechanics
Back to Physics World