Geodesic Deviation
Back
to Physics World
Back
to Geometrical Math for GR
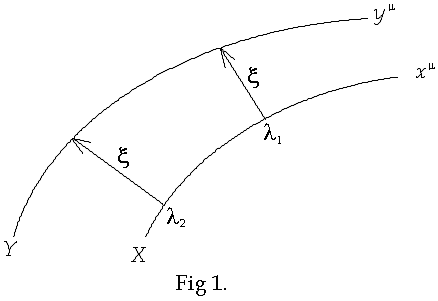
The purpose of this web page is to derive an expression for the equation of geodesic deviation. [1][2] Consider two test particles in free-fall whose geodesics are infinitesimally close to each other and which are initially parallel. A test particle in free-fall moves on a geodesic in spacetime. Spacetime curvature manifests itself through geodesic deviation. The relative acceleration of the test particles is also known as tidal acceleration. This page describes the meaning of this term and derives the equation for geodesic deviation. Geodesic deviation is defined as the relative separation of two infinitesimally close geodesics. Let x be the separation 4-vector of the two test particles. This vector is referred to elsewhere as the separation vector [3], the deviation vector [4], as well as the connecting vector [5]. This vector originates on one test geodesic and terminates on another, infinitesimally close, geodesic. Let each geodesic be parameterized by the affine parameter l. Two such nearby geodesics are shown below in Fig. 1 where the separation 4-vector x is shown

In Fig. 1 the geodesics
are labeled X and Y and described by the coordinates xm(l)
and ym(l)
respectively, each of which satisfies the geodesic equation. The 4-vector, x(l),
shown in the figure points from xm(l)
to ym(l)
and represents the relative separation of geodesics. Let the components of the
4-vector x be
xm. Then
![]()
Since X and Y
are infinitesimally close to each other it follows that x
really is a 4-vector (for the same reason that dxm
is a 4-vector). Our task is
to evaluate the second total derivative of the components of x.
The first total derivative is given by
![]()
The components of the
first derivative have the value
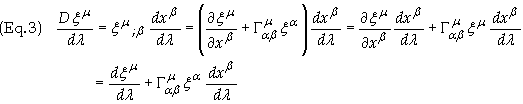
The second total derivative is found by applying the total derivative once more to Dxm/dl, i.e.
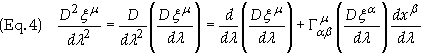
Substituting Eq. (3) into
(4) gives
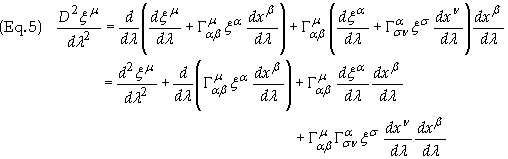
The second term on the
right side of the last equation can be expanded as follows
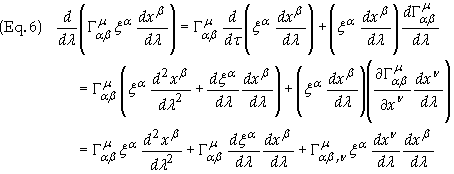
Substituting this result
into Eq. (4) gives

Since xb(l)
is a geodesic it follows that the expression d2xb/dl2
can be replaced with
![]()
Substitution of Eq. (8)
into (7) gives
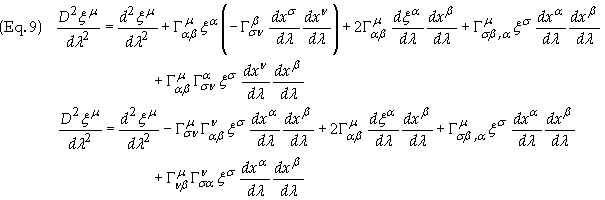
The goal at this point is to find an expression for the first term on the right hand side of Eq. (9). The geodesic equation for each geodesic is
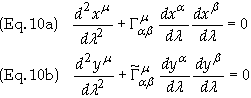
where the tilde over G
in Eq. (10b) means that it is evaluated on the Y geodesic where the G
is evaluated on the X geodesic. By employing a Taylor series expansion on
the G in Eq. (10b) it can be expressed to first order in xn, as
![]()
To obtain an expression in terms of xm subtract Eq. (9a) from Eq. (9b) to obtain
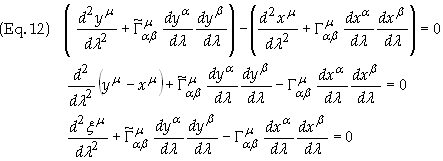
Substitute ym = xm + xm into Eq. (12) to obtain
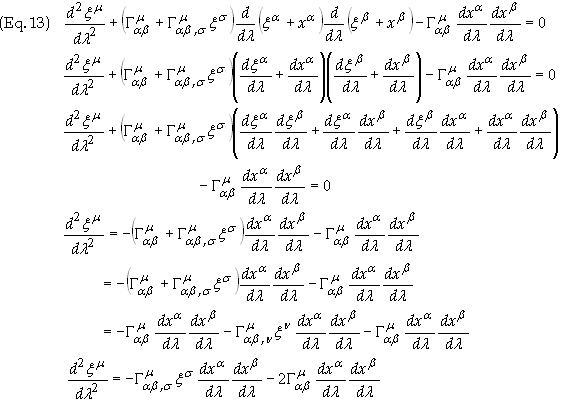
In the last expression of
Eq. (13) only first-order terms in xm
are kept. Substituting Eq. (13) into Eq. (9) yields
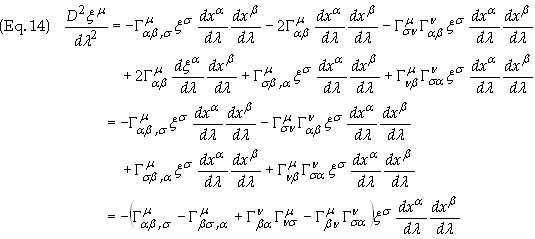
The Riemann tensor
is defined as [6]
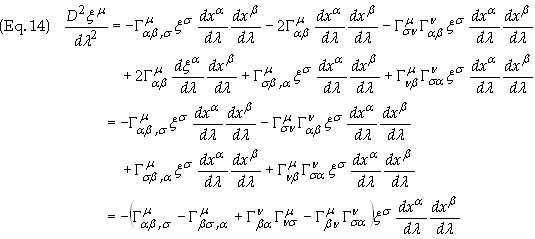
Substituting this expression for the Riemann tensor into Eq. (13) yields the final result
![]()
Eq. (15) is known as the equation
of geodesic deviation. In geometric form this expression can be written in
terms of the second derivative of x
as
![]()
References:
[1] Gravitation and
Spacetime – Second Ed., Hans C. Ohanian and Remo Ruffini, W.W. Norton
& Co., (1994), pages 341 to 343.
[2] A Short Course in General Relativity, J. Foster and J.D. Nightingale,
(1994), pages 113 to 114.
[3] Gravitation, Misner, Thorne and Wheeler, W.H. Freeman and Co.,
page 267.
[4] General Relativity, Robert Wald, The University of Chicago Press,
page 46.
[5] A first course in general relativity, Bernard F. Schutz, Cambridge
University Press, page 172.
[6] Ref. 3, page 219.