Poynting’s
Theorem
Physics
World
Back to Electrodynamics
In this web page the expression for the conservation of energy, as it applies to both fields and particles is derived. We start with the Lorentz force law. The infinitesimal work done on element of charge dq is the dot product of the force F on the element with the infinitesimal displacement dr of the element. The work done equals the infinitesimal change in the total mechanical energy Emech of the system, i.e.
![]()
Let r
represent the charge density of a system of charged particles for which are so
numerous and densely packed that we may consider the system as a continuum of
charge. Then upon substituting dq = rdV’
into Eq. (1) and using the expression for the current density vector J =
rv, Eq.
(1) can written as
![]()
Integrating
this over a volume V gives the total rate at which the fields in the
volume V are doing work on the particles in V, i.e.
![]()
Recall
the following two of Maxwell’s equations
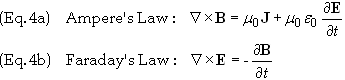
Take the
dot product of Eqs. (4a) and Eq. (4b) with E and B, respectively,
to obtain
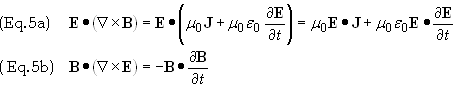
Subtract
Eq. (5b) from Eq. (5a) to obtain, upon dividing through by m0,
the result
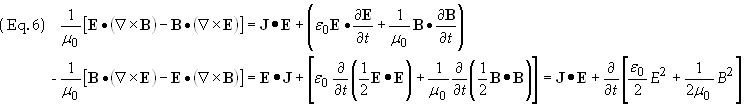
Eq. (6)
can be simplified by employing the vector identity Ñ·(E´B)
= B·(Ñ´
E) - E·(Ñ´
B). Using this
identity Eq. (6) becomes
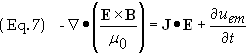
where uem
is defined as
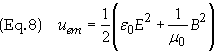
and
represents the total electromagnetic energy density of the electromagnetic (EM)
field. This expression was derived for the static fields and it is assumed that uem
has the
same meaning for time-varying fields. The quantity
![]()
is
called the Poynting vector and represents energy flow.
Substituting Eqs. (8) and (9) into Eq. (7) gives, upon rearranging terms
![]()
The
physical meaning of Eq. (10) is that the time rate of change of electromagnetic
energy within a certain volume, plus the time rate of energy flowing out through
the boundary surfaces of the volume per unit time, is equal to the negative of
the total work done by the fields on the matter within the volume. This is a
statement of energy conservation. I.e. the work done per unit volume by the
fields (E, B) is a conversion of electromagnetic energy into
mechanical energy. Solving Eq. (10) for J·E
and substituting the resulting expression into Eq. (3) yields
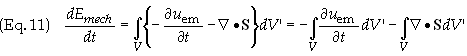
Eq. (11)
can be simplified by taking the partial derivative with respect to time outside
the first integral on the right, thus making it a total derivative, then using
the divergence theorem on the last integral, replacing a integral over the
volume V, by an integral over the surface bounding the volume V
resulting in
![]()
Let
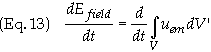
Efield
is the
total energy of the electromagnetic field of the Then Eq. (12) becomes
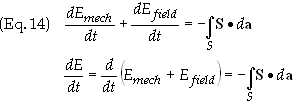
Eq.
(14) is known as Poynting’s theorem. The physical meaning of our result
is; the rate at which work is being done on the charges within the volume V
by the electromagnetic field on the charged particles equals the decrease in
energy of the field less the energy that flowed out through the surface.
Let Efield
represent the total electromagnetic field energy within V. Then the total
energy of the system is E = Emech
+ Efield.
This suggests that we identify the quantity u = umech
+ uem
as the total energy density. Since Eq. (14) must hold for all possible
electromagnetic fields it follows that
![]()
This is
the differential form of Poynting’s theorem and has the form of a conservation
law.