Momentum
of Radiation
Physics
World
Back to Electrodynamics
The following derivation of the momentum of
radiation is a common one found in many text books on electrodynamics. [1][2][3]
The Lorentz force law is given by
![]()
In order to consider continuous charge
distributions we will need to consider the infinitesimal force on a charge
element. The infinitesimal force, i.e. the force on an infinitesimal amount of
charge dq, has the value
![]()
The Lorentz force density f
is defined as the force per unit volume, which is the ratio of the
infinitesimal force, which is exerted on an infinitesimal charge element, over
the volume of the charge element, i.e.
![]()
where r
º dq/dV is
the charge density. The current density J is related to the charge
density r
and the velocity v by J = rv.
Upon substitution of these equalities into Eq. (3) we get
![]()
We’d like to express Eq. (4) solely in terms
of the field quantities. To accomplish this we note that r
and J
can be eliminated from Eq. (4) by using two of Maxwell’s equations, namely
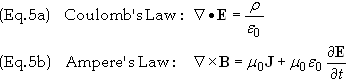
Solving for
r
and J gives
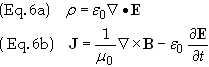
Substituting Eqs. (6) into Eq. (4) gives
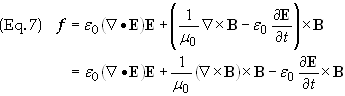
Note that
![]()
And from
![]()
Eq. (8) becomes
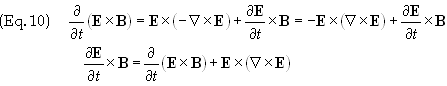
With this equality we can now express Eq. (7)
as
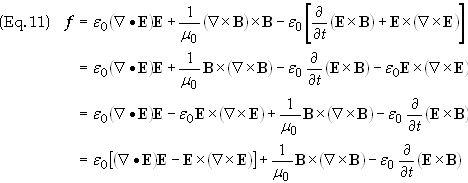
In order to facilitate further steps in this
calculation it will prove helpful to express Eq. (10) in a form symmetric in E
and B. Since the divergence of B vanishes in all possible
cases (with the possible exception of the presence of magnetic monopoles, which
as of yet there is no evidence of their existence) we can add
Ñ·B/m0
to right side of Eq. (11) without
changing the equality.
![]()
Now substitute the equalities
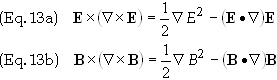
Into Eq. (12) to get
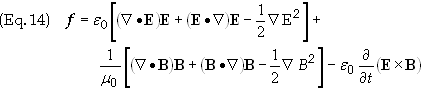
The
Maxwell stress tensor, Tjk,
is defined as
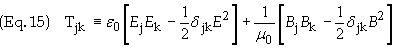
It can be shown that Tjk
has the
following property
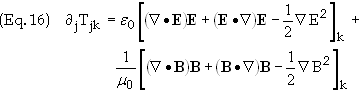
where
¶j º
¶/¶xj.
Einstein’s summation convention is employed:
summation over repeated indices is implied, the summation being over the
range the index takes on. Using this and the definition of the Poynting vector, S
= E´B/m0,
Eq. (14) thus
becomes
![]()
We can express Eq. 17 in vector form using dyad
notion. Let the Maxwell stress tensor be expressed as T. The kth
component of the dot product of T with a vector a is
![]()
The quantity ¶j
is the kth component of the operator Ñ
i.e. ¶j
= Ñj.
Therefore
![]()
With this notation Eq. 16 becomes
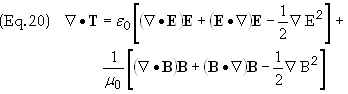
Eq. (17) can now be written in vector form
![]()
Integrating over all space gives
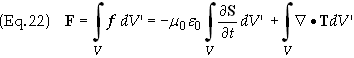
The
divergence theorem can be employed to change the second volume integral on the
right side of Eq. (22) to a surface integral. Letting pem
º
m0e0S.
Eq. (22) becomes
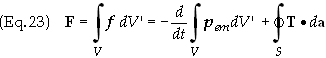
The first integral on the right can be written
as
![]()
The
force F in Eq. (23) is the total mechanical force of the field on the
charges and as such we can write F = dPmech/dt.
Let P º
Pmech
+ Pfield.
We can now write Eq. (23) as
![]()
We
can now interpret our results. The quantity pem
is the density of the momentum of the electromagnetic (EM) field meaning that Pfield
is the total momentum of the EM field. The integral on the right side represents
the rate at which momentum is flowing into the region bound by the surface S.
Eq. (25) thus states that the increase in momentum of the matter inside the
surface bound by S is equal to the decrease in the moment in the fields,
less the momentum flowing out of the surface S.
References:
[1] Classical
Electrodynamics 3rd ed. J.D. Jackson, John Wiley & Sons,
(1999). Pages 260 to 262.
[2] Introduction to Electrodynamics, David J. Griffith, Prentice-Hall,
Inc. (1981). Pages 292 to 293.
[3] Classical Electromagnetic Theory, Jack Vanderlinde, John Wiley
& Sons, Inc. (1993). Pages 81 to 86.
Back
to Electrodynamics
Physics World