Covariant Gauge Transformation
Physics
World
Back to Electrodynamics
Non-Covariant
Treatment of Gauge Transformations
The
vector potential, a, is defined such that
Since
the curl of the gradient of any continuous vector field vanishes then it follows
that the vector potential is, apart from an additive constant, arbitrary up to
the gradient of an arbitrary differentiable scalar field Y(x,
y, z, t). I.e. the quantity a’ defined as
also
satisfies Eq. (1) yielding the same magnetic field B, i.e.
In terms
of the Coulomb potential, f, and
the vector potential,
a
, the electric
field can be expressed as
The curl
of Eq. (3) results in Faraday’s law. Since the electric field is uniquely
defined when both its divergence and curl are specified within a bound region it
follows from the Helmholtz theorem that E is unique. Therefore E
cannot change upon a gauge transformation and is thus independent of Y.
If the potential, f,
is also modified then E will remain unchanged by the substitution a’
®
a + ÑY.
It is readily shown that the
substitution
leaves E unchanged
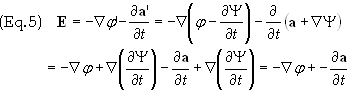
Therefore
E remains unchanged by the transformation. The transformation
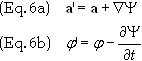
is
called a gauge transformation.
Upon a quick inspection of Eq. (5b) it may appear
that the Coulomb potential can be made to vanish and thus play no role in
describing the electric field. Upon a closer inspection this turns out not the
case. For the Coulomb potential to vanish by a gauge transformation we must have
or
. Eq. (4) then becomes
Substituting
we once again obtain
An interesting question would be; what happens to the Lagrangian and the
total energy of the particle, defined through the energy function, upon a gauge
transformation. The Lagrangian for a charged particle moving in an
electromagnetic field is [1]
Upon
making the gauge transformation in Eq. (5) we anticipate a new Lagrangian. Call
this Lagrangian L’. Then
Substituting
Eq. (5) we obtain
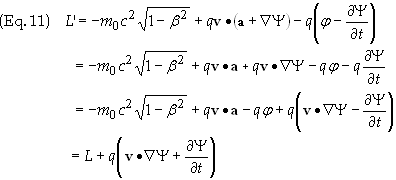
The
quantity on the right is simply the differential of Y,
i.e.
Therefore
Eq. (10) reduces to
Since
the term on the right is simply the total derivative of an arbitrary
differentiable function of space and time it drops out of Lagrange’s
equations. Thus if L’ satisfies Lagrange’s equations then so too does
L. Lagrange’s equations for L are
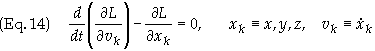
Let F
= qY and note
that F = F(x, y, z, t). Substitute the new Lagrangian into
Lagrange’s equations to obtain
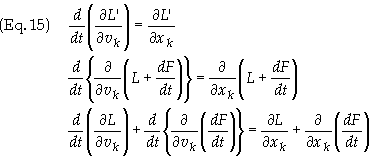
dF/dt
can be expanded as
The
second term inside the braces on the left hand side of Eq. (14) reduces to
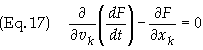
The
second term on the left hand side of Eq. (14) then becomes
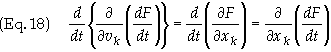
Substituting
back into Eq. (14) we obtain
Canceling
common terms results in the same Lagrangian that we started out with, i.e. Eq.
(13). Eq. (13) can be written as
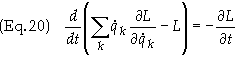
The
quantity in braces, i.e.
is known
as the energy function. When L does not depend on time explicitly
it follows from Eq. (19) that h is a constant of motion. For this reason h
is sometimes referred to as Jacobi’s integral. [2] h has the
same numerical value as the Hamiltonian, H. The only difference is that
the energy function is expressed as a function of
whereas
the Hamiltonian is expressed as a function of (qk, pk)
. Eq. (20) takes on a simpler
form if we substitute the canonical or generalized momentum,
pk,
conjugate to xk
defined as
It must
be noted that the L in Eq. (21) is not L’. It is what is
left of L’ after the total derivative dF/dt has been subtracted,
i.e. L = L’ - dF/dt. In terms of the canonical momentum
the energy function has the form
Substituting
the value of L from Eq. (8) into Eq. (21) we find
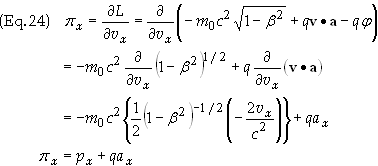
Substituting
this expression for pk
into Eq. (13) gives
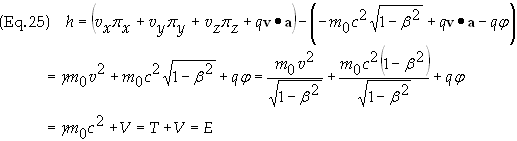
T
º
gm0c2 is
the inertial energy of the particle, aka the free-particle
energy. Thus the value of the energy function is the total energy of
the particle. If the Lagrangian is not an explicit function of time then the
total energy of the particle is a constant of motion. Also, from Lagrange’s
equation it follows that
Therefore
if the Lagrangian is not an explicit function of time then the canonical
momentum is a constant of motion.
Gauge
transformations can also be treated in the covariant formalism of Maxwell’s
equations. The 4-potential, A, is defined as
The Faraday tensor F is defined in terms of A as
It is
readily shown that the Faraday tensor remains unchanged by the gauge
transformation
Y(xa) is
an arbitrary differentiable function scalar field defined on spacetime.
Substituting into Eq. (27) yields
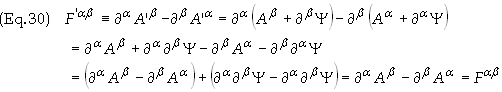
Therefore
the Faraday tensor remains unchanged under the gauge transformation in Eq. (28).
It is trivial to see that even though a gauge can be selected such that A0
= 0 the Coulomb potential remains untouched in the actual expression for
the Faraday tensor and hence the electric field remains unaltered. The covariant
Lagrangian, L, for a
charged particle in an electromagnetic field is [3]
U is
the particles 4-velocity. Upon making a gauge transformation we have
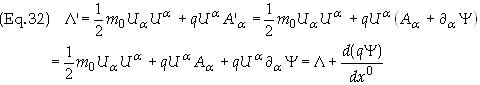
In a
manner similar to that above for the non-covariant Lagrange’s equations the
last term on the right is simply a differentiable function of (ct, x, y, z)
and will drop out of the covariant form of Lagrange’s equations, i.e.
Similar
to the non-covariant case, the canonical 4-momentum, Pm,
is defined as
With the
Lagrangian in Eq. (30) the canonical 4-momentum becomes
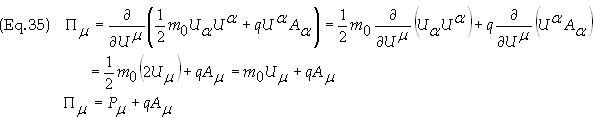
The
temporal component of the canonical 4-momentum, P0,
is
Therefore
the total energy is proportional to the time component of the canonical
(covariant) 4-momentum. If the Lagrangian, L,
is independent of t then it follows from Eq. (32) that the total energy
is a constant of motion.
References:
[1] Classical
Mechanics – 3rd Ed., Goldstein, Poole and Safko, Addison
Wesley, 2002, page 314, Eq. (7.141).
[2] Ref 1, page 61, Eq. (2.53).
[3] Ref 1, page 322, Eq. (7.165)
Back
to Electrodynamics
Physics World