Calculus of Variations

Back to Physics World
Back to Analytical Mechanics

Consider a function (where ). The integral

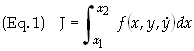
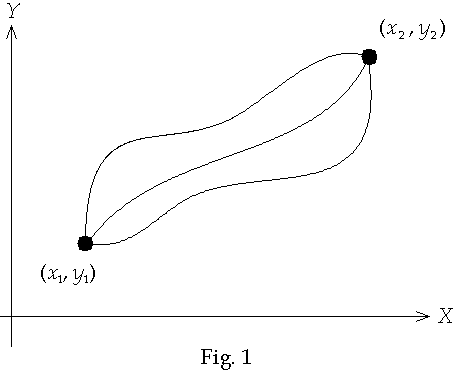
is called a functional. It is a generalization of the concept of a function in that it maps functions to numbers. The value of the integral depends on the function f, the function y � y(x), and the two end points x₁, x₂. Fig. 1 shows an example of various paths between two points.

The basic problem in the calculus of variations is finding a function y = y(x) such that the integral J[y(x)] has a stationary value on a given interval, I = [x₁, x₂]. That is to say that when y(x) is replaced with y(x) + e(x), J remains unchanged to first order in e provided that e is sufficiently small. The function e(x) must vanish at the end points, i.e. e(x₁) = e(x₂) = 0. y(x) is referred to as the correct path y(x) +e(x) as a neighboring path. The variation can be placed in a more familiar form by letting

where h(x₁) = h(x₂) = 0 and h(x) are well-behaved functions (continuous and nonsingular on I). It follows that J, as defined in Eq. (1), will also be a function of a, i.e.

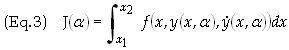
The condition for obtaining a stationary point is

Our first step is to employ Leibnitz’s rule for differentiation under the integral sign, i.e.

Applied to Eq. (3) gives

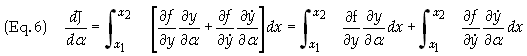
The second integral on the right side

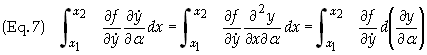
can be integrated by parts as follows. Recall the rule for integrating by parts, i.e.

Eq. (7) can be placed in this form by letting

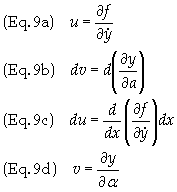
then

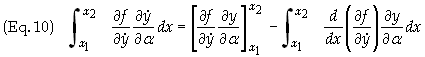
Evaluating the first term can be done by finding the partial derivative from Eq. (2), i.e.

By definition h(x₁) = h(x₂) = 0. Therefore the first term on the right side of Eq. (10) vanishes. Substituting these results into Eq. (6) gives

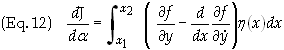
Setting this to zero implies that the first part of the integrand must vanish since h(x) is arbitrary. Therefore we get our final result

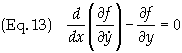
The above derivation can readily be extended to a function of several variables, i.e. to yield

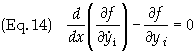
Eqs. (14) are known as the Euler-Lagrange differential equations.

Back to Analytical Mechanics
Back to Physics World