In 1977 the American computer magazine Kilobaud published a set of standard speed tests for the new wave of personal computers running BASIC. With slight modifications these were adopted by the UK publication Personal Computer World and the so-called benchmark timings accompanied all their computer reviews through the early 1980s.
(More recently, now that most home PCs are not supplied with BASIC, more supposedly 'realistic' benchmarks testing graphics performance and speed of running common applications have been used instead.)
There were eight benchmarks and in outline the programs were:
| Benchmark 1 | |
|---|---|
| 10 | For K=1 To 1000 |
| 20 | Next K |
| 30 | Stop |
| Benchmark 2 | |
|---|---|
| 10 | K=0 |
| 20 | K=K+1 |
| 30 | If K<1000 Goto 20 |
| 40 | Stop |
| Benchmark 3 | |
|---|---|
| 10 | K=0 |
| 20 | K=K+1 |
| 30 | A=K/K*K+K-K |
| 40 | If K<1000 Goto 20 |
| 50 | Stop |
| Benchmark 4 | |
|---|---|
| 10 | K=0 |
| 20 | K=K+1 |
| 30 | A=K/2*3+4-5 |
| 40 | If K<1000 Goto 20 |
| 50 | Stop |
| Benchmark 5 | |
|---|---|
| 10 | K=0 |
| 20 | K=K+1 |
| 30 | A=K/2*3+4-5 |
| 40 | Gosub 200 |
| 50 | If K<1000 Goto 20 |
| 60 | Stop |
| 200 | Return |
| Benchmark 6 | |
|---|---|
| 10 | K=0 |
| 20 | Dim M(5) |
| 30 | K=K+1 |
| 40 | A=K/2*3+4-5 |
| 50 | Gosub 200 |
| 60 | For L=1 To 5 |
| 70 | Next L |
| 80 | If K<1000 Goto 30 |
| 90 | Stop |
| 200 | Return |
| Benchmark 7 | |
|---|---|
| 10 | K=0 |
| 20 | Dim M(5) |
| 30 | K=K+1 |
| 40 | A=K/2*3+4-5 |
| 50 | Gosub 200 |
| 60 | For L=1 To 5 |
| 70 | M(L)=A |
| 80 | Next L |
| 90 | If K<1000 Goto 30 |
| 100 | Stop |
| 200 | Return |
| Benchmark 8 | |
|---|---|
| 10 | K=0 |
| 20 | K=K+1 |
| 30 | A=K^2 |
| 40 | B=ln(K) |
| 50 | C=sin(K) |
| 60 | If K<1000 Goto 20 |
| 70 | Stop |
The benchmarks might need to be tweaked slightly to suit particular dialects of BASIC, e.g. using 'Let' and 'Then' and typing commands in all UPPERCASE.
The principle was that a simple series of instructions was timed for 1000 repeats, and the time taken in seconds for each benchmark reported. If the BASIC were especially fast it might be necessary to run each benchmark several times and take the average, or increase the number of repeats to 10,000 then divide the time by 10, to obtain sufficiently accurate timings.
Each benchmark was designed to test a particular aspect of the computer's BASIC, and the average time for the eight tests depended on both the efficiency of the BASIC and the inherent speed of the machine's processor.
It occurred to me that the benchmark programs are simple enough that they could be run on many programmable calculators; though the actual program listings might look very different since calculators do not generally use BASIC as such, they can be made to perform the same operations in the same way.
This would give a means of comparing the running speeds of the calculators, both to each other and to early personal computers, and might be an interesting investigation.
The first programmable calculators, from the 1970s, were based on the contemporary scientific models and had a single line display, initially of light-emitting-diode type and later of liquid crystal type, and generally could only display numerals, not letters. This of course meant that it was not possible to display 'prompts' for input values, or to label output, and as a result more complex programs were hard to use since you had to remember what you were expected to enter at stage, and what the answers meant.
There were a few single-line calculators which could display text (the HP-41C and Casio FX 602P for example), but in the late 1980s a new type of calculator emerged. These were the graphing calculators and had a (relatively) large screen designed as a dot-matrix, typically around 80 dots wide by 50 dots high or more. This was mainly intended to allow the calculator to plot graphs but also permitted display of text characters over several lines, at least 6 lines of 14 characters say. Immediately this improved the usability of the calculators. Expressions could be displayed in full for confirmation as they were entered before pressing the 'equals' key, and programs now could provide brief prompts to the user, and state what the answer represented. (It seems all graphing calculators are programmable.) Being able to see several lines of program at once also made the process of programming them considerably easier.
The programming model of calculators normally belongs to one of two types.
Some of the changes which typically had to be made to the benchmarks to allow them to run in 'calculator language' were:
Eleven different programmable calculators were available for these tests, spanning manufacturing dates from 1977 to 2005 and program storage capacity from 32 steps to 190 kilobytes. A brief description of each calculator follows. The accompanying pictures show the calculators at their correct relative sizes.
Introduced 1977. Keystroke programmable.
One of the first low-cost programmable calculators. It includes an adequate range of scientific functions and is very compact. (Only 19 keys so most have three functions.) However it was clearly designed down to a price and is of flimsy mechanical construction. The sliding on/off switch is liable to lose contact momentarily if pressed while turned on (losing the stored program) and the keys are prone to bounce.
Programs are limited to 36 steps, there is only one memory and the only conditional statement is 'go if negative' which performs a branch if the number in the display is less than zero.
For the benchmark tests:
Introduced 1977. Keystroke programmable.
This is primarily an advanced scientific calculator with two-variable statistics, and only secondly a programmable. It is quite large and of fairly robust construction, though again with an occasional tendency to key bounce resulting in double entries.
It has a mere 32 program steps, no conditional instructions at all (so the only way to terminate a loop is to force a mathematical error, e.g. by taking the reciprocal of zero) and the only jump instruction is back to the start of the program. It has 8 memories though.
Problems when running the benchmarks were:
Introduced 1983. Keystroke programmable.
This is specifically an advanced programmable model, though also including a good range of scientific functions. It allows up to 512 program steps, depending on the number of memories in use, and has a full range of looping instructions (the DSZ type) and conditional branches. It has indirect memory addressing to simulate arrays.
Points about running the benchmarks were:
Introduced 1992. Formula programmable.
In some ways this seems to be the replacement for the TI-66. It has approximately 1500 bytes of memory, equivalent to around 1000 steps on the TI-66, and uses alphanumeric variable names rather than numbered memories.
The basic 'program' unit is the formula, which at its simplest can be just a single equation which is evaluated and returns a value. However formulas can also be multi-statement and include simple program commands such as 'If' and 'Goto', and can call other formulas as subroutines. Text prompts are possible.
The TI-67 is one of the most powerful scientific/programmable calculators produced other than the graphical display types. It was also quite cheap and appears robust enough, though the rubber mat keyboard has a very poor feel.
Problems running the benchmarks were:
Introduced 1992. BASIC-like programming.
This is one of the most usable graphic calculators produced. It has 32 kilobytes of total memory (approx. 28K available to the user) and a quite complete programming language. Unusually it permits multi-character variable names (too many other calculators limit variables to the single letters A to Z) and allows the programmer to make full use of the function keys and onscreen menus. It appears to have been designed for real-world use rather than for school teaching, and an updated version, the TI-86, is apparently still on sale in 2008.
All the benchmark programs could be run essentially as listed earlier, without problems. The calculator is well-made and pleasant to use.
Introduced 1991. Intermediate between keystroke programming and a separate programming language.
This was an early and relatively cheap graphics calculator. It is odd in that only the left half of the display is a full dot matrix, for drawing graphs at quite low resolution, while the right half is for text only, on a single line, plus various indicator symbols. Program memory is only 400 bytes (but programs tend to be compact so a reasonable amount can be achieved in this space), there are 26 variables (A to Z) and up to 10 separate programs can be stored, memory space permitting.
The FX-6300G is really very limited as a graphical model, though it has an extensive range of mathematical/scientific functions and has the advantage of being much smaller (especially thinner) than 'normal' graphic calculators. The keyboard is quite crowded and difficult to read.
Interestingly, the same basic design of calculator, in different cases and with a few extra functions but retaining the split display, is still being sold by Texet, Citizen and even Hewlett-Packard in 2008. (But not by Casio!)
When running the benchmarks:
Introduced 1995? BASIC-like programming.
An updated version of this model (mainly a restyled case) is currently the entry-level Casio graphing calculator. Its graphing capabilities are adequate but not outstanding (there seems to be no way to perform operations such as finding intercepts or maxima/minima of drawn graphs) and it has a reasonable but not extensive range of mathematical functions.
The programming language is fairly complete and there were no difficulties in running the benchmarks, though a curious omission is that there is no way to delete a single program – only to delete all the programs at once!
There is 32 kilobytes of total memory with about 20K available for use. The FX-7400+ uses 'modes' of operation, e.g. normal calculation mode, graphing mode, statistics mode, table mode. This is probably to simplify initial learning but does tend to interfere with exchange of data from one mode to another.
Another problem is that many of the functions, which one might expect to find shortcuts to on the keyboard, are in fact only obtainable by pressing the 'OPTN' key, scrolling through then selecting a function class (numeric, angle etc.) with the function keys, then scrolling and selecting again to obtain the actual function. This makes it difficult to find a particular function and involves numerous keypresses. To compound the problem some menus are different in program mode from normal mode.
On the plus side the keyboard is very uncluttered and easy to read, the screen is clear (though not of particularly high resolution) and the case looks like it would stand up to rough use.
Introduced 1996. BASIC-like programming.
This model has around 30 kilobytes of user memory and in many ways is a much improved version of the FX-7400+. It does have graph operations like intercepts and areas under curves, more graph types (polar, conics) and extra maths functions. The screen resolution is higher too.
The CFX-9850G's unique feature is that it is the only pocket calculator with a colour display. Text and graphs can be shown in blue, green or orange, on the light greenish yellow LCD background. This sounds like a handy feature since it would allow multiple superimposed graphs to be coloured to help distinguish them, and program prompts and output could be colour-coded.
Colour can sometimes be useful, but the colour display is not without its problems. It is not immediately obvious how to actually set the colour of text or graphics and it requires navigating the menus. Secondly it is essential to set the colour intensities and overall contrast very carefully or the different colours can be almost indistinguishable or, especially in the case of orange, almost invisible. Finally the display is not quite as distinct as it ought to be and text often appears to have a border around it. Overall the colour is probably more of a gimmick than a must-have feature.
As for the FX-7400+, the CFX-9850G uses modal operation and it also has a clear keyboard with quite positive key action. The manual is long but, as is almost invariably the case, somewhat confusingly written.
Overall the CFX-9850G represents a worthwhile improvement on the FX-7400+ and is a good choice of general purpose calculator, with few omissions or limitations. However the similar FX-9750G or FX-9860G, with monochrome displays, would likely be just as good. As usual with Casios the build quality of the CFX-9850G is high. (The battery cover is retained with a chromed screw threading into a brass insert!)
Introduced 1998. BASIC-type programming.
The EL-9400 has 32 kilobytes of memory with around 20K available to the user. It is a graphing calculator with a fairly high resolution and quite clear screen, and easy to use graphing operations. Its only 'modes' are normal operation, graph drawing, and statistics editing.
One unusual feature is that it can be set so that calculations and formulas are displayed in standard textbook format, rather than on a single line, as they are are entered. This can be very helpful as a way to check that a formula has been entered correctly.
For instance the display might show
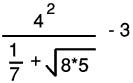
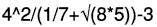
The range of graphing and mathematical functions is fairly comprehensive, a little beyond the Casio FX-7400+. Omissions are absence of complex numbers and number bases. Statistical functions are quite good but reference to the manual may be needed to configure them, and statistics graphing can be tricky to set up.
Rather than using 'function keys' below the screen labelled on the bottom line of the display, the EL-9400 mostly uses two-tier menus where the first selection, for the general class, is made by pressing a letter key and the individual functions are chosen by a number. (Or the cursor keys and Enter can be used to navigate menus.) This works well in practice and has the advantage that more menu options are visible on screen at once, reducing the need for scrolling.
The EL-9400 has an especially neat appearance and all the key legends are a good size and easy to read. The key action is positive and pleasant.
Of course it is not without its faults. The main complaint is the very limited programming language. There is no scope for positioning text on the text screen; each item just goes on the next line. There are no looping instructions as such at all and instead all loops have to be explicitly programmed via 'Goto' and 'Label'. Finally the only statement which can follow an 'If' test is 'Goto' or 'Gosub', so programs end up poorly structured.
In running the benchmarks:
Introduced 1999. BASIC-type programming.
The EL-9600 can be thought of as the EL-9400's bigger brother, in more ways than one. It is physically slightly longer and wider and though both models have exactly the same key layout, the EL-9600's keys are fractionally larger. This makes the key legends even easier to read.
The screen resolution of the EL-9600 is higher than that of the EL-9400, and indeed of most other graphics calculators, though the screen is physically about the same size so characters are actually a little bit smaller. 32 kilobytes of total memory are fitted but again only around 20K is available when 'equation editor' mode is used.
The EL-9600 has all the features of the EL-9400 but adds complex numbers, polar graphing, matrix operations, a general equation solver, simultaneous equation solver, financial calculations and even more graphing operations. There is little this calculator cannot tackle, though as always seems to be the case the manual is a bit confusing on some features.
The unique feature of the EL-9600 is that it has a touch-sensitive screen, operated with the fitted stylus. This can be used to select menu options or position the cursor on the graph or editor screen. An interesting idea for a calculator if you remember about it, and can speed up entry, but not essential when the keyboard-controlled menu selection system works so well. The current top-of-the-range Sharp graphing calculator, the EL-9900, does not have a touch screen.
The two failings of the EL-9600 are that it shares the same limited programming language as the EL-9400 (this has been improved in the EL-9900), and the screen contrast is poor, making text difficult to read under dim lighting. This is strange since the EL-9400 has a very clear display. Probably the screen overlay needed for touch operation partially blocks the screen, making the background darker.
Overall though, despite a few niggles, the EL-9600 is a very capable and usable calculator.
Introduced 2003. BASIC-style programming.
The hp39g+ has a large memory of 192 kilobytes available to the user, though this is not quite as much as it sounds because programs are stored as plain text rather than in tokenised format, and also as a semi-compiled version for running. The result is that a typical program takes up about three times as much memory on the hp39g+ as on the Casio CFX-9850G for instance.
This calculator has a large number of built-in functions, including complex numbers, matrices, calculus and equation solving. Its display is large, clear and high in resolution by calculator standards.
The main unusual feature of the hp39g+ is its use of 'aplets', which are somewhat similar to the 'modes' of the Casio graphing calculators. There are predefined aplets for function graphing, parametric and polar graphs, equation solving, financial calculations and inferential statistics. Unlike the Casios however, the hp39g+ allows the user to make copies of the standard aplets under new names, complete with the equations and data which have been entered, for use at a later date. It is also possible to create completely new aplets with user programming, which operate almost like the standard ones.
The programming language is fully featured and includes 'Repeat' and 'While' loops and multi-statement 'If...Then...Else..End' constructs. Unfortunately the syntax can be a little idiosyncratic (use of semicolons as parameter separators rather than commas) and the manual does a poor job of explaining the syntax, some of the examples given actually being incorrect. There is no Goto command at all so 'Do...Until' was used in all the benchmark tests requiring a Goto.
Most graphics calculators include a socket for a cable to connect to another calculator of the same model, or to a desktop computer, for storing or downloading data and programs to save having to type them in manually. Usually the necessary cable is an optional extra, not easy to obtain, and often expensive for the calculator to PC cable.
An excellent feature of the hp39g+ is that it is supplied with a USB cable for connection to a recent model PC, and software suitable for Windows 98 and presumably later versions. There is also an infrared link for communication with another hp39g+. This is much better than the situation with Sharp where a calculator-to-PC cable costs £30, about half the price of the calculator itself.
The hp39g+ has one major design flaw though, and that is its keyboard. The 'shifted' functions are printed in mid orange on a light blue metallic effect background, and there is simply not enough contrast. The labels can be almost impossible to read under artificial lighting except by tilting the keyboard sideways to make the background less reflective. Very poor ergonomics by Hewlett-Packard standards.
To make matters worse the keys themselves have an unusually stiff and 'clicky' action, and occasionally click down without being registered. The effect is reminiscent of 1970s calculators and somehow the design does not give the impression it would stand up to really long-term use.
Nonetheless the hp39g+ is a very powerful calculator, one of the most advanced except for those with computer algebra, and was relatively cheap at the time (with cable included.) The current updated version, the hp39gs, significantly has a different colour scheme with much more contrast between the fascia and the key legends.
Finally, the benchmark timings themselves. Run times are given in seconds for 1000 iterations of the main loop, though in practice for the slower calculators some benchmarks were timed for only 100 repeats then multiplied by 10.
Where it was impossible to run a particular benchmark on a given calculator because a required programming feature was not available, an estimate of how long it would have taken if it were possible is shown in brackets, extrapolated from the results for other calculators plus the benchmarks which could be performed. This makes it possible to calculate a sensible average of the eight benchmark times for each calculator.
| Calculator Make and Model | Time to Complete Benchmark (1000 iterations) in Seconds | Number of Times Slower than ZX Spectrum | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Average BM1 to 8 | BM1 | BM2 | BM3 | BM4 | BM5 | BM6 | BM7 | BM8 | ||
| Sinclair ZX Spectrum | 56 | 4 | 8 | 20 | 19 | 23 | 53 | 78 | 239 | 1.0 |
| Sinclair Cambridge Programmable | 776 | 216 | 216 | 366 | 412 | 510 | (880) | (1200) | 2410 | 13.9 |
| Texas TI-51-III | 2197 | 455 | 636 | 1648 | 1467 | (1800) | (3100) | (4300) | 4171 | 39.2 |
| Texas TI-66 | 3210 | 296 | 1154 | 2711 | 2352 | 2913 | 5033 | 6896 | 4328 | 57.3 |
| Texas TI-67 | 897 | 199 | 199 | 467 | 401 | 463 | 1686 | (2400) | 1364 | 16.0 |
| Texas TI-85 | 48 | 3 | 16 | 36 | 33 | 39 | 58 | 95 | 102 | 0.9 |
| Casio FX-6300G | 75 | 5 | 18 | 55 | 56 | 59 | 104 | 152 | 148 | 1.3 |
| Casio FX-7400+ | 68 | 4 | 21 | 59 | 61 | 69 | 95 | 112 | 126 | 1.2 |
| Casio CFX-9850G | 65 | 4 | 21 | 58 | 60 | 67 | 92 | 108 | 111 | 1.2 |
| Sharp EL-9400 | 133 | 37 | 37 | 67 | 68 | 78 | 262 | 365 | 151 | 2.4 |
| Sharp EL-9600 | 174 | 48 | 48 | 89 | 90 | 103 | 346 | 478 | 188 | 3.1 |
| Hewlett-Packard hp39g+ | 79 | 2 | 36 | 41 | 40 | 49 | 61 | 319 | 87 | 1.4 |
Notice that the first row in the table is for the Sinclair ZX Spectrum home computer, launched in mid 1982. At the time this was the best-selling personal computer in the UK, and with a Z80A microprocessor, 16 or 48 kilobytes of RAM, a fairly high resolution display and programmable in BASIC, its specification was not too dissimilar to today's high-end graphics calculators (though of course the Spectrum lacked specialised graphing functions and the more advanced maths commands.)
From the column headed 'Number of Times Slower than ZX Spectrum' it can be seen that several of the tested calculators do indeed operate at a comparable speed to the Spectrum – these are the Texas TI-85; Casio FX-6300G, FX-7400+ and CFX-9850G; and Hewlett-Packard hp39g+. In fact the TI-85 is actually slightly faster than a Spectrum; this calculator is known to use a version of the Z80 microprocessor itself.
The Sharp EL-9400 and EL-9600 are noticeably slower than the previously mentioned calculators. Partly this is attributable to their lack of dedicated 'For' loops; needing to explicitly program an increment, test and jump makes a big difference in benchmarks 1, 6 and 7.
It is strange that the EL-9600 is consistently about 30% slower than the EL-9400, when they appear to be based on very similar hardware and use an identical programming language. Is there a difference in processor clock speed, or is there an extra overhead in scanning the touch screen?
The Hewlett-Packard hp39g+ is the second fastest overall, but considering that it uses a 32-bit ARM9 processor clocked at 75MHz, and converts its programs to semi-compiled form, the wonder is that it is not many times faster than the ZX Spectrum, with its 8-bit Z80A CPU at 3.5MHz and interpreted BASIC. Apparently the hp39g+'s operating system was originally written for the Hewlett-Packard Saturn microprocessor and has to run on the ARM via an emulator, but even so there must be some gross inefficiencies in the implementation to make it quite so slow. It underlines how well designed the TI-85 is that it achieves a faster speed with a much less powerful microprocessor.
The other four (non-graphing) calculators are all considerably slower than the graphing models. Their common feature is that they use chipsets specifically designed for calculators, or as general purpose microcontrollers, whereas graphics calculators mostly employ separate microprocessors (e.g. Z80, 68000, ARM types) which were originally designed for desktop computers. Even the Texas TI-67, despite being a relatively late model from 1992, falls into the slowish microcontroller category.
It is rather a surprise that the Sinclair Cambridge Programmable, despite being one of the first programmables and obviously a very cheap design, is actually the fastest of the four non-graphing models. However it is known that the accuracy of its mathematical functions (sin, ln, square root etc.) is quite low, so perhaps some of the speed is obtained by running the iterative approximations for fewer repeats.
The Casio FX-6300G seems to be an exception to the above – it utilises a custom controller yet is almost as fast as the best microprocessor-based models. It must have a well optimised design.
Overall the benchmark results show what huge variation in speed exists between different models of programmable calculator – a factor of over 60 between the TI-66 and TI-85.
The results also show that, as might be expected, more recent models tend to be faster than older models, though the trend is by no means continuous or clear-cut.
|
