Para volver al menú principal pulse sobre la palabra

Límites estadísticos de tolerancia

Esquema:

1. Límites independientes de la distribución

2. Límites cuando se muestrea una población normal

1. Límites independientes de la distribución

Definición

Si D es la proporción de observaciones de la variable aleatoria que se encuentra entre los límites L₁ y L₂ que son funciones univaluadas de las observaciones de manera tal que:

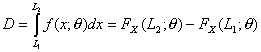
Entonces L₁ y L₂ reciben el nombre de límites estadísticos de tolerancia.

Ya que L1 y L2 son funciones univaluadas de las observaciones, son variables aleatorias. A su vez D es también una variable aleatoria y la proposición  P ( D≥

 d) =γ se interpreta como que la probabilidad de que la proporción de valores de X entre L₁ y L₂ no sea menor que d, es igual a γ.

Sean X_(r) y X_{(n-r +1)} el r-ésimo valor más pequeño y el (n-r +1)-ésimo valor más grande en una muestra aleatoria de tamaño n la cual involucra a la variable de medición X.

Se ha demostrado que la proporción de valores D que se encuentra entre L₁ = X_(r) y L₂ =  X_{(n-r +1)} tiene una distribución Beta con parámetros α=n-2r+1 y  β =2r., sin importar la forma de la función de densidad de X, en donde L₁ y L₂ son de orden simétrico. De esta forma

expresión muy fuerte que permite, conocidas 3 de las cantidades n, r, d y γ, determinar la cuarta usando la distribución beta.

La principal utilidad de la formula es la de determinar el tamaño mas pequeño de la muestra de manera tal que con una probabilidad  γ por lo menos una proporción d de la distribución de X se encuentre entre los extremos X₍₁₎ y X_(n). Es decir, para r=1

lo que puede simplificarse para obtener

Por ejemplo, si se obtiene una muestra de tamaño 25 de una distribución con función de densidad desconocida, la probabilidad de que por lo menos un 80% de los valores de X se encuentre entre los dos valores extremos de la muestra es de 0,973.

Muchas veces se buscan límites de tolerancia unilaterales de tal manera que la probabilidad de que por lo menos una proporción d de la distribución de X sea más grande que un límite de tolerancia inferior o menor que un límite de tolerancia superior, sea γ. Puede demostrarse, sin importar la distribución de X, que

Si r = 1, la inferencia se formulará con respecto al valor mas pequeño de la muestra. Si r = n, con respecto al más grande. Si r = 1

[Volver al principio]

2. Límites de tolerancia cuando se muestrea una población normal

Recuérdese que los límites estadísticos de tolerancia colocan límites sobre las mediciones que se llevan a cabo sobre una distribución, a diferencia de los intervalos de confianza, los cuales determinan a aquellos intervalos donde es probable que se encuentre un parámetro desconocido.

Supóngase que se consideran los estimadores

dado que son variables aleatorias, están sujetas a la variabilidad en el muestreo.

Considérese el intervalo aleatorio

siendo k una constante.

Es posible elegir k de manera que si se toman repetidamente muestras del mismo tamaño, una proporción γ de las mismas contendrá por lo menos un 100 d % de los valores de la distribución.

Con base en una muestra de tamaño n los límites de tolerancia bilateral de un 100 γ % para un porcentaje de un 100 d % de una distribución normal son

en donde γ es el coeficiente de confianza y d es el alcance. Los valores de k se encuentran tabulados para distintos valores de n, γ y d.

Muchas veces solo tienen interés los límites de tolerancia unilaterales

valores que también se encuentran tabulados.

Ejercicio.

En un medio muy competitivo, la disponibilidad de un producto con respecto a la demanda es crucial para el éxito del negocio. Para determinar un límite de tolerancia superior para la demanda mensual de cierto producto, un centro comercial ha recolectado lo que cree es una muestra aleatoria de las demandas mensuales y la cual consiste en los siguientes datos: 129, 142, 145, 153, 136, 138, 163, 151, 146, 128, 133, 148, 144, 140, 143.  Si la demanda mensual de este producto se encuentra aproximada en forma adecuada por una distribución normal, determínese un limite de tolerancia superior con  γ=0,99 y d=0,95.

Solución

Calculamos la media y la desviación típica muestral ( Cuasi-Desviación típica)

El valor de k que se obtiene en la tabla, para n=15, γ=0,99 y d=0,95 es k=3,102.

Por tanto el límite de tolerancia superior es:

142,6 + (3,102)(9,2798)=171.39. Es decir, con 172 unidades por mes se tendrá una alta seguridad de satisfacer la demanda mensual de este producto.

[Volver al principio]