|
Para volver al menú principal pulse sobre la palabra |
|---|
1. En una población de 1.000
individuos se establecen dos grupos, A y B. Los cocientes intelectuales de ambos
grupos se distribuyen según N(100,30) y N(120,35), respectivamente. Elegido,
aleatoria e independientemente, un individuo de cada grupo, se pide:
a) ¿Cuál es la probabilidad de
que el individuo del grupo A tenga
un cociente intelectual superior a 90?
b) ¿Cuál es la probabilidad de que el individuo del grupo B tenga un cociente intelectual superior a 90?
c) ¿Cuál es la probabilidad de
que ambos tengan un cociente intelectual superior a 90?
Sea X la variable aleatoria que mide el coeficiente de inteligencia de la población A, y sea Y la variable aleatoria para el coeficiente de la población B.
a) Nos piden la p[X>90]. Tipificando la variable:
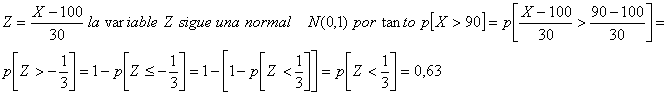 b) La probabilidad p[Y>90], se calcula de manera análoga tipificando la
variable.
b) La probabilidad p[Y>90], se calcula de manera análoga tipificando la
variable.
![]() c) Nos piden p[(X>90)Ç(Y>90)],
como ambas variables son independientes, la probabilidad pedida es el producto
de ambas, por tanto: p[(X>90)Ç(Y>90)]=
p[(X>90)] .p[(Y>90)]=0,63.0,8043=0,5067.
c) Nos piden p[(X>90)Ç(Y>90)],
como ambas variables son independientes, la probabilidad pedida es el producto
de ambas, por tanto: p[(X>90)Ç(Y>90)]=
p[(X>90)] .p[(Y>90)]=0,63.0,8043=0,5067.
2. Las alturas de los individuos de
dos poblaciones A y B siguen distribuciones normales de media 1,70 metros y de
desviaciones respectivas s1, s2
con (s1<s2 ) Cuando se
escoge un individuo al azar de cada población, di en cuál de las dos
poblaciones es más probable que el individuo elegido mida entre 1,68 m y 1,72
m. Razona la respuesta.
Sea X la variable aleatoria que mide la altura de los individuos de la población A y sea Y la variable que mide la altura de los individuos de la población B. X sigue una N(1,70; s1) e Y sigue una normal N(1,70; s2); con (s1<s2 ) para ver cuál de estas probabilidades es mayor: p[1,68<X<1,72] y p[1,68<Y<1,72] ; tipifiquemos ambas variables y comparemos.

Puesto que el intervalo
1º es más amplio que el 2º y ambas variables son normales N(0,1).
Intuitivamente es claro,
como tienen la misma media, el porcentaje de individuos que se concentra
alrededor de la media es tanto mayor cuanto más pequeña sea la dispersión de
los individuos alrededor de la media, es decir, la desviación típica. Por
tanto, para un mismo intervalo centrado en la media, el área bajo la curva de
la normal, será tanto mayor cuanto más pequeña sea la desviación típica.
3. Se ha comprobado que determinada
prueba cultural es superada por el 70% de las personas con estudio de grado
medio y por el 55% de las personas con estudios primarios. Un total de 10
personas (seis con estudios de grado medio y cuatro con estudios primarios)
realizan dicha prueba cultural. Calcular:
a) La probabilidad de que
exactamente cuatro de las personas con estudios de grado medio superen la
prueba.
b) La probabilidad de que al menos
una de las personas con estudios
primarios supere la prueba.
c) Si consideramos la variable «número de personas que superan la prueba entre las 10 que la realizan», ¿seguiría un modelo binomial de probabilidad? Razona la respuesta.
a) Podemos suponer que
el número de éxitos para las 6 personas con estudios de grado medio sigue un
modelo binomial con n =6 y p =0,7. La probabilidad de tener exactamente 4 éxitos
vendría dada por:
![]()
b) Análogamente para las 4 personas con estudios primarios. Sea X el número
de éxitos
![]()
c) No,
pues una de las condiciones del modelo de binomial es que la probabilidad de éxito,
en cada prueba, permanezca constante.
4. En recientes estudios realizados sobre pacientes portadores del SIDA se ha podido determinar que el 70% consume algún tipo de drogas. En la sala de espera de una consulta especializada en esta enfermedad se encuentran en un determinado momento seis personas. ¿Cuál es la probabilidad de que ninguno haya consumido drogas?
La variable X sigue una
binomial de parámetros n=6 y p=0,7. Por tanto, la probabilidad p[X =0] =0,36=0,000729.
5. Según informó DIARIO 16 el día 22 de noviembre de 1992, de un total de 2.847 asuntos presentados en el Tribunal Constitucional en el período 1-1-1991 hasta 31-10-1992, sólo se han podido resolver 2.147, lo que equivale aproximadamente al 75% de los presentados. ¿Cuál es la probabilidad de que de diez asuntos elegidos al azar todos hayan sido resueltos?
Sea X la variable aleatoria que nos da el número de éxitos en 10 pruebas. X sigue un modelo binomial de parámetros n =10 y p =0,75. La probabilidad p[X=10] =0,7510 =0,0563
6. Según un informe de la OCDE, en el año 1981 el 35% de la población mundial tenía menos de 15 años. Si fuera posible elegir una muestra aleatoria de la población mundial formada por diez personas, ¿cuál es la probabilidad de que a lo sumo haya tres individuos con edad inferior a 15 años?
Sea X la variable
aleatoria “número de individuos cuya edad es inferior a 15 años en una
muestra aleatoria de 10 individuos”. X sigue una binomial de parámetros n =10
y p =0,35. La probabilidad que nos piden es p[X £ 3]=p[X=0]+p[X=1]+p[X=2]+p[X=3]=
![]()
7. En un test destinado a medir la capacidad espacial de un grupo de alumnos de la Escuela de Arquitectura se ha podido saber que el 20% tienen una capacidad espacial insuficiente. ¿Cuál es la probabilidad de que de tres alumnos elegidos al azar los tres hayan dado resultados insuficientes en el test?
Sea X la variable
aleatoria que da el número de éxitos (el éxito aquí es tener capacidad
espacial insuficiente) en las 3 pruebas. X sigue una binomial de parámetros n=3
y p=0,2. Por tanto, la probabilidad p[X=3]=0,23=0,008.
8. Supongamos que la probabilidad de nacer varón en España es de 0,512. Si durante un año en una determinada región se han producido 2.000 nacimientos, ¿cuál es la probabilidad de que el número de varones esté entre 1.000 y 1.080?
Sea X la variable
aleatoria “número de nacidos varones en 2000 nacimientos”. X sigue una
binomial de parámetros n=2000 y p=0,512. Como n es un número suficientemente
grande, la distribución binomial puede aproximarse por una distribución normal
de media n.p y desviación típica (n.p.q)1/2 . Por tanto, la
variable X sigue una normal N(1024, 22,35);
luego la p[1000<X<1080] =p[1000,5<X<1079,5] = 0,9935-0,1465=0,847.
9. En un centro escolar se ha observado que el 55% de los alumnos superan unas determinadas pruebas de psicomotricidad. Si este porcentaje es constante, y teniendo en cuenta que se pasa la prueba a 100 alumnos, hallar la probabilidad de que la superen exactamente más de 50.
El número X de alumnos
que superan la prueba de los 100 presentados sigue una binomial de parámetros
n=100; p=0,55. Como n.p es grande, esta distribución se puede aproximar por una
normal de media n.p y desviación típica (n.p.q)1/2. Luego X sigue
una normal N(55, 4,975). La probabilidad p[X>=50,5]=1-p[X £
50,5]=0,8171.
10. El porcentaje de fracaso
escolar en Bachillerato, en una determinada región, es del 40%. Sobre un total
de 1.000 individuos:
a) ¿Cuál es la probabilidad de
que se produzcan exactamente 400 fracasos?
b) ¿Cuál es la probabilidad de
que no superen los 400 fracasos?
X sigue una binomial de
parámetros n=1000; p=0,4. Distribución que se puede aproximar por una normal
N(400; 15,492). Teniendo en cuenta que como variable discreta tiene sentido
hablar de p[X=400]; pero como variable continua no tiene sentido. Se conviene en
considerar que la p[X=400]=p[399,5<X<400,5]=0,5129-0,4871=0,0258.
b) Análogamente,
para calcular la p[X<400], calculamos la p[X£399,5]=0,4871.
11. Hallar el primer y el tercer cuartil en una distribución N(25,3).
El primer cuartil será
el valor x 0,25 de la variable aleatoria tal que p[X<x 0,25]=0,25,
es decir que deja a la izquierda de la curva a un cuarto de la población.
Tipificando la variable:
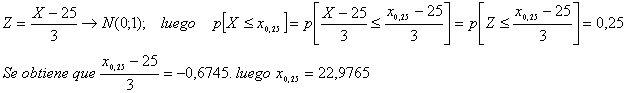 Análogamente para el cuartil tercero p[X<x 0,75]=0,75; se obtiene
x 0,75=27,0235
Análogamente para el cuartil tercero p[X<x 0,75]=0,75; se obtiene
x 0,75=27,0235
12. Un almacén de camisas ha
determinado que el cuello de, los varones adultos se distribuye normalmente con
media 38 cm y desviación típica 1,5 cm. Con el fin de poder preparar la
producción de la próxima temporada, y teniendo en cuenta que su producción
está en 10.000 camisas:
a) ¿Cuántas camisas de los números
35, 36, 37, 38 y 39 tendrán que
fabricar?
b) ¿Cuántas camisas habrán de
fabricar del 43? e) ¿Y del 33?
Sea X la variable
aleatoria que mide el cuello de los varones adultos. X sigue una normal N(38;
1,5).
a) La p[X=35] es nula;
pero puede considerarse que los hombres que utilizan la talla 35 van a ser
aquellos varones cuyas medidas de cuello estén comprendidas entre 34,5 y 35,5.
Por tanto, asignamos la talla 35 a todos aquellos cuya
p[34,5<X<35,5]=0,0478- 0,0098=0,0380= 3,8%. Para la talla 36 consideramos
la p[35,5<X<36,5]=0,1586-0,0478=0,1106. Para la talla 37
p[36,5<X<37,5]=0,3694-0,1586=0,2108. Para la talla 38:
p[37,5<X<38,5]=0,6306-0,3694=0,2612. Y, para la talla 39:
p[38,5<X<39,5] =0,8413 – 0,6306=0,2107.
Como son 10.000 el número
de camisas que se van a fabricar, se harán 380 de la talla 35; 1.106 de la
talla 36; 2.108 de la talla 37; 2.612 de la talla 38 y 2.107 de la talla 39.
b) De la talla 43, se
fabricarán p[42,5<X<43,5]=0,9999-0,9986=0,0013; se fabricarán 13 y de la
talla 33: p[32,5<X<33,5]=0,0014-0,0001=0,0013, se fabricarán 13.
13. En la asignatura de psicología
evolutiva se ha podido determinar que las calificaciones se distribuyen según
una N(5,5; 1,2).
a) ¿Entre qué valores, en torno a
la media, se encontrará el 95% de
los alumnos?
b) ¿Entre qué valores, en torno a
la media, se encontrará el 50% de
los alumnos?
e) ¿A partir de qué nota se
encontrará el 10 por 100 de los
alumnos mejor calificados?
a) Se trata de calcular
el intervalo tal que:
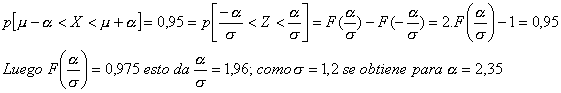
Por tanto el intervalo
pedido es (5,5-2,35; 5,5+2,35)=(3,15; 7,85); es decir entre 3,15 y 7,85.
b)

Por tanto el intervalo
pedido es (5,5-0,8094; 5,5+0,8094)=(4,6906; 6,3094); es decir entre 4,6906 y
6,3094.
c) Hay que calcular el
valor de x tal que P[X>x]=0,1; es decir: p[X £ x]=0,9;
este valor se corresponde con 7,0379
14. La distribución de
sociabilidad de un colectivo sigue una distribución normal de media 20 y de
desviación típica o estándar 2. Si elegimos un individuo al azar, hallar:
a) La probabilidad de que tenga un
coeficiente como máximo de 25.
b) La probabilidad de que tenga un
coeficiente entre 22 y 25, sabiendo
que éste está por encima de 21.
c) ¿Dónde habría que poner el
valor de la variable para hacer dos grupos (menos sociables, más sociables),
con la condición de que en el primer grupo estuvieran el 30% del colectivo, y
en el segundo el 70% restante?
Sea X la variable
aleatoria que mide el coeficiente de sociabilidad, X sigue una N(20; 2). Por
tanto:
a) p[X
£25]=0,9938.
b)
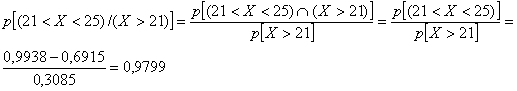
c) El valor de la
variable es el valor x tal que p[X<x]=0,3. Tal valor se corresponde con
18,9512.
15. El peso de los adultos de una
población numerosa se distribuye normalmente con media 65 kg y desviación típica
3 kg. Se eligen dos individuos al azar. Calculando las correspondientes
probabilidades, justifica qué es más probable:
a) Que cada uno de los individuos
tenga un peso comprendido entre 63,5 y 66,5 kg.
b) Que uno de ellos tenga un peso
comprendido entre 62 y 68 kg y el otro tenga un peso no comprendido entre 62 y
68 kg.
Sea X la variable
aleatoria resultado de elegir un individuo al azar y pesarlo; X sigue una normal
N(65; 2). Sea Y la variable
aleatoria resultado de elegir otro individuo al azar y pesarlo; Y sigue una
N(65; 2). Evidentemente, X e Y son independientes. Por tanto:
a) p[(63,5<X<66,5)Ç(63,5<Y<66,5)]= p[(63,5<X<66,5)].p[(63,5<Y<66,5)]=[0,7734-
0,2266]2=0,54682=0,2990.
b)
p[(62<X<68)Ç( (Y £ 62)È(Y ³
68))] = p[(62<X<68)].p[( (Y £ 62)È(Y ³
68))] =0,8664.(1-0,8664)=0,1157.
Es mas probable el caso
a).
16. En una manzana de casas hay 10
aparcamientos. En cada aparcamiento puede encontrarse o no un automóvil con
independencia de lo que ocurra en los otros. Si la probabilidad de que un
aparcamiento esté ocupado es de 0,4; se pide:
a) Identificar y describir el
modelo de probabilidad.
b) Calcular la probabilidad de que
en cierto día se encuentren ocho automóviles aparcados.
Sea X la variable
aleatoria “número de aparcamientos ocupados de los 10 existentes”. X sigue
una binomial de parámetros n=10; p=0,4.
a) X sigue B(10; 0,4).
b) p[X=8]=45. 0,48.
0,62 = 0,0106
17. Se sabe que dos poblaciones
distintas, X e Y, se distribuyen normalmente
con media 0. Además:
p[X³
2] = p[Y³ 3] =
0,1587 Se pide que calcules sus respectivas varianzas.
Sea X una variable
aleatoria N(0; s1)
e Y otra variable N(0; s2).
De p[X³
2] = 1-p[X<2] y p[Y³ 3]=1-p[Y<3]; obtenemos
p[X<2]=0,8413 y p[Y<3]=0,8413.
Sea Z1 =X/s1
y Z2 =Y /s2;
las variables Z1 y Z2 son N(0; 1); por tanto p[X<2]=0,8413
equivale a p[Z1<(2/s1)]=0,8413;
de donde 2/s1=0,9998
y de aquí s1=2,0004.
De otro lado, p[Y<3]=0,8413 equivale a que p[Z2<(3/s2)]=0,8413;
de donde 3/s2=0,9998
y de aquí que s2=3,0006.
18. Un ascensor admite como peso máximo
300 kg. La población de usuarios tiene un peso que se distribuye según una ley
normal de media 70 kg y desviación típica 10 kg.
Calcula la probabilidad de que
cuatro personas cualesquiera de dicha población que suban al ascensor superen
el peso máximo.
Sea X1; X2;
X3; X4 cuatro variables aleatorias N (70; 10)
correspondientes al peso de cada una de las personas que suben al ascensor; la
variable aleatoria Y = X1+ X2+ X3+ X4
sigue una distribución normal de media E[Y] y desviación típica [Var(Y)]1/2.
Como E[Y]= E[X1]+ E[X2]+ E[X3]+ E[X4]=4.70=280.
y Var(Y)= Var[X1]+ Var[X2]+ Var[X3]+ Var[X4]=4.102=400;
luego, la desviación típica de Y: sy=(400)1/2=20.
Por tanto Y sigue una N(280; 20). La probabilidad de que p[Y>300]=1-p[Y £ 300]=1-0,8413=0,1587.
19. El peso (en gramos) de una
pieza fabricada en serie se distribuye según una normal de media m
= 52 y desviación típica s = 6,5.
a) Hallar la probabilidad de que
una pieza fabricada pese más de 68
gramos.
b) Si el 30 por 100 de las piezas fabricadas pesa mas que una pieza dada. ¿Cuánto pesa esta última?
Sea X la variable
aleatoria; X sigue una N(52; 6,5).
a) p[X>68]=0,0069.
b) Sea xp el
peso de la pieza. P[X>xp]=0,3; luego, p[X
£ xp]=0,7 de donde xp
=55,4086.
20. Un examen tipo test consta de
diez preguntas, las cuales tienen cuatro posibles respuestas, siendo solo una de
ellas correcta. Si una persona contestase al azar , es decir, eligiese de forma
aleatoria una de las cuatro respuestas posibles de cada una de las 10 preguntas:
a) ¿Cuál sería el número
esperado de respuestas correctas?
b) ¿Qué probabilidad tendría de
acertar la respuesta correcta de al menos seis preguntas?
c) ¿Qué probabilidad tendría de no contestar ninguna pregunta correctamente?
Sea X la variable
aleatoria “número de respuestas correctas de las 10 preguntas”. X sigue una
binomial B(10; ¼) es decir B(10; 0,25).
a) La E[X] =n .p
=10.1/4=10/4=2,5.
b) p[X ³ 6]
que es igual a:
![]()
c) p[X=0]=0,7510=0,0563
21.
Se sabe que un determinado medicamento produce mejoría de cierta enfermedad a dos de cada tres pacientes.
Se les administra a siete enfermos.
a) Calcular la probabilidad de que
mejoren cuatro
b) Calcular la probabilidad de que mejoren al menos cuatro personas.
Sea X la variable
aleatoria número de éxitos del medicamento en 7 pacientes. X sigue una
binomial de parámetros n=7; p=2/3: B(7; 2/3).
![]()
![]()
22. En un restaurante se sabe que
la duración sin rotura de las copas en uso sigue una distribución normal. Se
sabe que las copas duran, por término medio, 50 días, con una desviación típica
de ocho días.
a) Calcular la probabilidad de que
una copa dure menos de 35 días.
b) Calcular la probabilidad de que
una copa dure mas de 60 días.
Sea X la variable
aleatoria “duración sin roturas, en días, de una copa”. X sigue una N(50;
8). a) p[X<35]=0,0304. b) p[X>60]=0,1056.
23. La probabilidad de que una
pieza, elegida al azar de una gran población de piezas, sea defectuosa es 0,25. Se extraen 5 piezas
a) Calcular la probabilidad de
obtener al menos una pieza
defectuosa.
b) Calcular la probabilidad de
obtener un número impar de piezas defectuosas.
c) Calcular la probabilidad de
obtener como máximo tres piezas
defectuosas.
d) Calcular el número medio de piezas defectuosas.
Sea X la variable
aleatoria “número de piezas defectuosas en una muestra de 5”. X sigue una
binomial B(5; 0,25)
a) p[X ³1]=0,7627
b) p[(X=1)È[(X=3)È[(X=5)]=0,3955+0,0879+0,0010=0,4844.
c) p[X£ 3]=0,9844
d) E[X] =n .
p=5.0,25=1,25.
24. La distribución de la duración
de un embarazo en es aproximadamente normal, con media 266 días y desviación típica
16 días. Calcular:
a) La proporción de embarazos con una duración máxima de
244 días.
b) Los percentiles del 25%, del 50% y del 75% de la distribución considerada y comenta su significado.
Sea X la variable
aleatoria “duración en días de un embarazo”. X sigue una N(266; 16).
a) p[X£ 244]=0,0846
b)
p[X<P25]=0,25 se obtiene P25=255,2081; p[X<P50]=0,5
se obtiene P50=266; p[X<P75]=0,75 se obtiene P75=276,7919.
25. Supongamos una distribución normal de media 50 en la que la probabilidad de obtener un valor por encima de 70 es 0,0228. ¿Cuál es la desviación típica? ¿Cuál probabilidad de los valores por debajo de 45?
Sea X una variable
aleatoria que se distribuye normalmente con N(50; s ). Si la p[X>70]=0,0228; se deduce que