|
Para volver al menú principal pulse sobre la palabra |
|---|
Si las variables aleatorias X1, X2, …, Xn tienen la misma función de probabilidad que la distribución de la población y su distribución de probabilidad conjunta es igual al producto de las marginales, entonces X1, X2, …, Xn forma un conjunto de n variables aleatorias independientes e idénticamente distribuidas (IID) que constituye una muestra aleatoria de la población.
La función (densidad) conjunta de probabilidad de X1, X2, …, Xn es la función de verosimilitud de la muestra dada por:
en donde
denota los datos muestreados.
Cuando las realizaciones de
se conocen, la función
depende
sólo del parámetro desconocido q.
Un parámetro es una característica numérica de la distribución de la población de manera que cuando se conoce esta, la distribución, queda descrita, sino total, al menos parcialmente.
Los parámetros o funciones de los parámetros se estiman a partir de la información contenida en una muestra.
Un estadístico es cualquier función de las variables aleatorias que se observaron en la muestra de manera que esta función no contiene cantidades desconocidas.
Si se utiliza un estadístico T para estimar un parámetro desconocido q, entonces T recibe el nombre de estimador de q y el valor específico que tome T, por ejemplo t, se denomina estimación de q.
La distribución de muestreo de un estadístico T es la distribución de probabilidad de T que puede obtenerse como resultado de un número infinito de muestras aleatorias independientes, cada una de tamaño n, provenientes de la población de interés.
Sea X1, X2, …, Xn un conjunto de n variables aleatorias independientes cada una con función generadora de momentos
Si Y=a1X1 + a2X2+ … + anXn en donde a1, a2, …, an son constantes, entonces:
Sea X1, X2, …, Xn un conjunto de variables aleatorias independientes y normalmente distribuidas con medias E(Xi) y varianzas Var(Xi)=si2 para i = 1, 2 , …, n. Si Y=a1X1 + a2X2+ … + anXn en donde a1, a2, …, an son constantes, entonces Y es una variable aleatoria normal con media
E(Y) =a1m1+ a2m2+ … + anmn
y con varianza
var(Y)= a12s21+ a22s22+ … + an2s2n
(La hipótesis de normalidad puede quitarse)
.Sea X1, X2, …, Xn una muestra aleatoria que consiste en un conjunto de variables aleatorias independientes e idénticamente distribuidas ( v.a IID) tales que E(Xi)=m y Var(Xi)=s2 para todo i.
Entonces el estadístico
se define como la media de las n v.a IID.
Aplicando el teorema 2 se tiene :
de donde
Sea X1, X2, …,
Xn una muestra aleatoria que consiste en un
conjunto de variables aleatorias independientes y normalmente
distribuidas tales que E(Xi)=m
y Var(Xi)=s2
para i = 1, 2, …, n. Entonces la distribución de la media muestral
es normal con media m
y varianza s2/n.
Un problema de máximo interés consiste en saber lo que ocurre si no se especifica la distribución de probabilidad de la población a partir de la cual se extrae la muestra.
Sea X1, X2, …, Xn una muestra aleatoria que consiste en un conjunto de variables aleatorias independientes e idénticamente distribuidas ( v.a IID) en una distribución de probabilidad no especificada y tales que E(Xi)=m y Var(Xi)=s2 para todo i. Entonces el promedio muestral
tiene una distribución de media m y varianza s2/n que tiende a una normal conforme n tiende a ¥
Debe de notarse el hecho de que si el modelo de probabilidad de la población es semejante a una distribución normal, la aproximación normal será buena aun para muestras pequeñas.
En general, para n>30, la aproximación normal será relativamente buena y puede emplearse
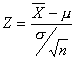
para hacer inferencias sobre m cuando se conoce el valor de la varianza poblacional s2.
Supongamos que la población se encuentra normalmente distribuida con m conocida y s2 desconocida. Se define S2 como
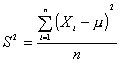
donde para cada i
Sea X1, X2, …, Xn una muestra aleatoria de una distribución normal de media m y varianza s2. La distribución de la variable aleatoria
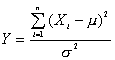
es del tipo de la Chi-cuadrado con n grados de libertad.
Desde un punto de vista práctico, la varianza muestral tal y como se encuentra definida anteriormente tiene poco uso, pues rara vez se conoce la media poblacional m. En su lugar se emplea la varianza muestral, definida por:
Más adelante se verá porqué se emplea el divisor n-1 en lugar de n.
El
reemplazo de la media desconocida m por la media muestral
da origen a la presencia de otro
estadístico en la definición de S2. Como consecuencia se tiene que
la distribución de muestreo
Sea X1 y X2 son variables aleatorias independientes y cada una tiene una distribución Chi-cuadrado con n1 y n2 grados de libertad, entonces Y = X1 + X2 tiene también una
Chi-cuadrado con n1 + n2 grados de libertad.
donde
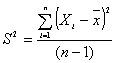
Demostración
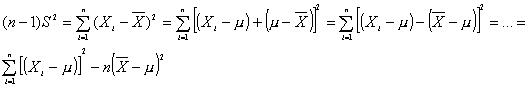
de donde
Dividiendo los dos miembros por s2
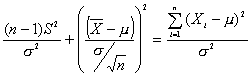
Por el teorema 5
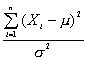
sigue una Chi-cuadrado con n grados de libertad y
de manera similar sigue una chi-cuadrado con 1 grado de libertad, dado que
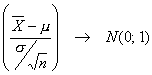
En vitud del teorema 6 se sigue que
Se sabe, cuando una muestra proviene de una distribución normal con desviación estándar conocida s, que la distribución de
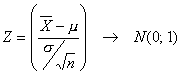
Generalmente el valor de s no se conoce y lo que se hace es reemplazar s por un estimador s, que es el valor de la desviación estándar muestral S.
Desafortunadamente
ya no es N(0; 1) aún cuando la muestra provenga de una distribución normal.
Sin embargo, es posible determinar la distribución muestral exacta de
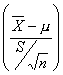
cuando la población es normal N(m, s) con m y s desconocidos.
Sea Z normal N(0, 1) y X una Chi-cuadrado con n grados de libertad. Si Z y X son independientes, entonces la variable aleatoria
sigue una t-Student con n grados de libertad.
La similitud de la t-Student y la N(0,1) es alta para valores grandes de n, sobre todo para n ³30.
Cuando se muestrea una población normal N(m,s) , el estadístico
sigue una t-Student con n-1 grados de libertad.
Supongamos que X sigue una N(mX, s) e Y una N(mY, s) donde X e Y son variables aleatorias independientes con varianzas iguales conocidas.
Sabemos que
Entonces
sigue una distribución normal de media mX-mY y varianza 12. s2/nX + (-1)2.s2/nY
Por tanto si se conoce el valor de s2, el estadístico
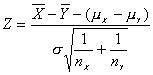
se distribuye según una normal de N(0; 1)
Se ha supuesto que s es conocido. Sin embargo, es poco probable que esto suceda. Por tanto para el caso en el que el muestreo se lleve a cabo sobre dos poblaciones normales independientes con varianzas iguales pero desconocidas, para cada una de las muestras obtenidas pueden definirse las varianzas muestrales definidas S2X y S2Y y dado que
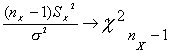
y teniendo en cuente el teorema 6
sigue también una chi-cuadrado con nX+nY-2 grados de libertad
Luego
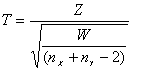
sigue una t-Student con nX + nY - 2 grados de libertad.
Por tanto
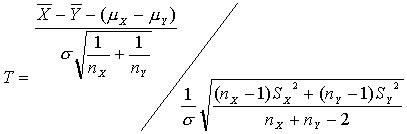
simplificando
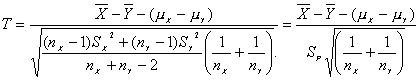
donde
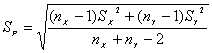
es un estimador combinado de la varianza.
Si suponemos que las varianzas poblacionales son distintas pero conocidas, entonces se tiene:
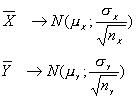
De donde
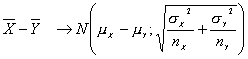
y por tanto
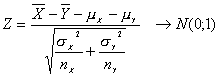
En el supuesto de que s2X y s2Y sean desconocidas y haya que estimarlas a partir de S2X y S2Y el problema se complica, en tal caso se tiene:
sigue una distribución t-Student con f grados de libertad, en donde f es la aproximación de Welch:
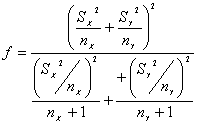
expresado en número entero.
La inferencias con respecto a la varianza s2 cuando se muestrea una población normal se formula con base a
En esta sección se formularán inferencias con respecto a la varianza de dos distribuciones normales independientes con base en las muestras aleatorias de cada una.
Sea X una variable aleatoria que se distribuye según una Chi-cuadrado con n1 grados de libertad e Y otra variable aleatoria independiente de X, que se distribuye según una Chi-cuadrado con n2 grados de libertad. Entonces la variable aleatoria
tiene una función de densidad de probabilidad dada por
Es fácil ver que si
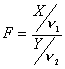
sigue una distribución F con n1 ,n2 grados de libertad, entonces F´=1/F sigue una F con n2 ,n1 grados de libertad
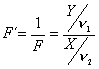
Es por esto que en las tablas sólo aparecen los valores cuantiles f1-a;n1;n2 para a<0.5. Si se desean los valores cuantiles para a>0.5
o bien
siendo
Volviendo al problema de desarrollar estadísticos para formular inferencias con respecto a las varianzas de dos distribuciones normales independientes.
Sean X1, X2, …., Xnx variables aleatorias independientes N(mX, sX)
Sean Y1, Y2, …, Yny variables aleatorias independientes N( mY, sY)
Si X e Y son independientes
entonces por el teorema 10
