|
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema
1. El intervalo de confianza para m, cuando se muestrea una distribución normal con varianza conocida
2. Intervalo de confianza para m cuando se muestrea una distribución normal de varianza desconocida.
3. Intervalos de confianza para la diferencia de medias cuando se muestrean dos distribuciones normales independientes.
4. Intervalo de confianza para s2 cuando se muestrea una distribución normal con media desconocida.
5. Intervalos de confianza para el cociente de dos varianzas cuando se muestrean dos distribuciones normales independientes.
6. Intervalos de confianza para el parámetro de proporción p cuando se muestrea una distribución binomial.
Pongamos un ejemplo para introducir el concepto de estimación por intervalo.
Una compañía decide que los últimos 36 meses han sido típicos en relación a la demanda de un producto, con base en los datos muestrales el valor calculado para la media muestral es de:
En otras palabras 200 es un valor estimado puntual de un parámetro desconocido, el cual representa la demanda promedio de este producto por la compañía. Este estimador, ¿implica que la demanda promedio desconocida no sea mayor de 250 ni menor de 150?. Esto no es posible saberlo, ya que no se tiene ninguna indicación del posible error en el estimado puntual.
Supóngase que la desviación estándar de la media muestral es 60. De acuerdo con el teorema central del límite
De esta forma la probabilidad de que
lo que equivale a que
Dado
que
es una variable aleatoria, el
intervalo
es un intervalo aleatorio y la probabilidad de que dicho intervalo contenga al verdadero valor de m, es de 0,95. En otras palabras si se obtienen muestras repetidas de la misma población y del mismo tamaño y se calculan los valores específicos para dicho intervalo; entonces debe esperarse que en un 95% de los casos estos intervalos contengan al valor de la media desconocida m.
Por otro lado, para los datos obtenidos de una sola muestra
sería incorrecto decir que la probabilidad de que m se encuentre en el intervalo
es de 0,95. Sin embargo, la probabilidad de 0,95 para el intervalo aleatorio sugiere que la confianza en que el intervalo (80, 320) contenga el valor de la media desconocida m es alta. Sólo en este sentido se permite asignar un grado de confianza a la proposición m se encuentra en el intervalo (80, 320) igual a la probabilidad del intervalo aleatorio
Así cuando se escribe
no se está formulando ninguna proposición probabilística en sentido clásico, sino más bien un grado de confianza.
En general, la construcción de un intervalo de confianza para el parámetro desconocido q consiste en encontrar un estadístico suficiente T y relacionarlo con otra variable aleatoria X=f(T;q), en donde X involucra a q pero la distribución de X no contiene a q, así como tampoco a ningún otro parámetro desconocido. Entonces se seleccionan dos valores x1 y x2 tales que:
en donde 1-a recibe el nombre de coeficiente de confianza. Mediante cálculo algebraico se puede modificar el contenido entre paréntesis y expresarlo:
El intervalo de confianza de q se obtiene sustituyendo en h1(T) y h2(T) los estimadores calculados a partir de la muestra, dando lugar a lo que se llama intervalos de confianza bilaterales. Al seguirse el mismo procedimiento pueden calcularse los intervalos de confianza unilaterales.
El intervalo de
confianza se calcula en base al mejor estimador de m,
la media muestral
.
Por tanto,
de manera que
y
en
donde f es la función de densidad de la distribución de muestreo
de
.
Dado que
y por tanto
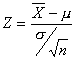
sigue una normal N(0; 1) se sigue:
Pero
se sigue que
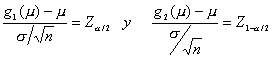
Despejando g1(m) y g2(m) se obtiene:
Teniendo en cuenta que Z a/2 es igual a –Z1-a/2 el intervalo queda de la forma:
Al manipular las desigualdades de dentro del paréntesis, se tiene:
Si se reemplaza la variable aleatoria por los datos calculados a partir de una muestra de tamaño n, un intervalo de confianza del 100(1-a)% para m, es:
Tamaño de
la muestra. Supóngase, en las mismas
condiciones de este ejercicio, que deseamos estimar el tamaño de la muestra de
manera que, con una probabilidad de 1-a,
la media muestral
se encuentre a una distancia
inferior a e
unidades de la media poblacional m.
De la expresión:
se obtiene
al resolver para n se obtiene:
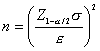
Una objeción muy severa a esta formula es que se requiere el conocimiento de la varianza poblacional s2. Si este no se conoce, una estimación muy burda para la desviación típica es igual a la sexta parte del recorrido de las observaciones, ya que para distribuciones unimodales la gran mayoría de las observaciones se encuentran a una distancia de 3 desviaciones estándar de la media.
Cuando se muestrea una población normal N(m,s) , el estadístico
sigue una t-Student con n-1 grados de libertad, donde
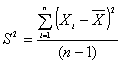
Por lo tanto es posible determinar el cuantil t1-a/2, n-1 de T, para el cual
Al sustituir T por su valor se obtiene
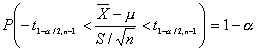
de donde
La probabilidad de que este intervalo aleatorio contenga a la media poblacional es de 1-a.
Para una muestra particular de tamaño
n, a partir de los valores estimados de
y de s2, un intervalo de
confianza del 100(1-a)% para m
es:
Sean X1, X2, …, XnX e Y1, Y2, …, Yny dos muestras aleatorias de dos distribuciones normales independientes.
Si suponemos que las varianzas poblacionales son distintas pero conocidas, entonces se tiene:
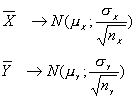
De donde
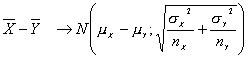
y por tanto
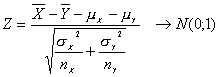
De esta forma es posible encontrar
el cuantil Z1-a/2,
tal que:
Sustituyendo Z por su valor y operando
Un intervalo de confianza para una muestra particular de tamaño n, viene dado por:
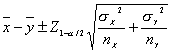
Para el caso en el que el muestreo se lleve a cabo sobre dos poblaciones normales independientes con varianzas iguales pero desconocidas
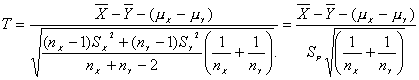
donde
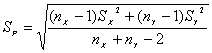
sigue
una t-Student con nX + nY –2 grados de libertad.
Un intervalo de confianza, para una muestra partícula al 100(1-a)% viene dado por:
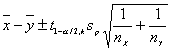
Donde sp es el valor obtenido para la muestra particular de Sp.
En el supuesto de que s2X y s2Y sean desconocidas y distintas y haya que estimarlas a partir de S2X y S2Y el problema se complica, en tal caso se tiene:
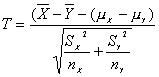
sigue una distribución t-Student con f grados de libertad, en donde f es la aproximación de Welch:
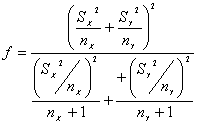
expresado en número entero.
La inferencias con respecto a la varianza s2 cuando se muestrea una población normal se formula con base a
Entonces es posible determinar los valores cuantiles
tales que:
y de aquí
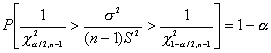
Con base en los datos de una muestra se pude calcular un intervalo de confianza al 100(1-a)%
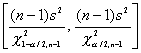
Sean X1, X2, …., Xnx variables aleatorias independientes N(mX, sX)
Sean Y1, Y2, …, Yny variables aleatorias independientes N( mY, sY)
Si X e Y son independientes
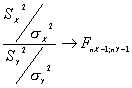
Es decir, el cociente sigue una F con nX-1, nY-1 grados de libertad.
Entonces puede escribirse:
donde a y b son los valores cuantiles
La probabilidad se puede expresar así:
De esta manera un intervalo de confianza del 100(1-a)% para sY2/sX2 está dado por
Puede demostrarse que el estimador de máxima verosimilitud del parámetro p, denotado por
donde X es binomial con parámetro n y p. Nótese que s u estimador insesgado de p, ya que
La varianza viene dada por:
Recuérdese que para n grande, la variable aleatoria
entonces puede demostrarse que la distribución de
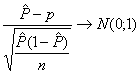
De esta forma, la probabilidad
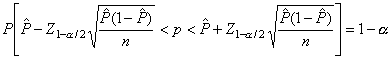
Para una muestra particular de tamaño n, un intervalo de confianza al 100(1-a)% viene dado por
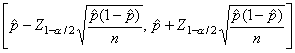
donde
el estimador de
se obtiene de la muestra:
Tamaño de muestra: Con
respecto al muestreo de una distribución binomial, un problema que surge de
forma frecuente, es el estimar el tamaño de la muestra necesario para que con
una confiabilidad del 100(1-a)%
el estimado del parámetro de proporción se encuentre a no más de e
unidades de p. Es decir
de donde se sigue que
Despejando
Se ha obtenido n en función de p, el parámetro que se desea estimar. Dado que este no se conoce de antemano, lo que de manera generalizada se hace es escoger el valor más conservador de n. Esto ocurre cuando la cantidad p(1-p) es máxima, es decir cuando p=1/2.