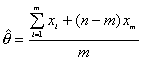|
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema
1. Estimadores insesgados.
2. Desigualdad de Tchebysheff.
3. Estimadores insesgados de varianza mínima.
4. Estadísticos suficientes.
5. Métodos de estimación puntual.
5.1 Estimación por máxima verosimilitud.
5.2 Método de los momentos
5.3 Estimación de máxima verosimilitud para muestras censuradas.
Sean X1, X2,
…, Xn una muestra aleatoria de tamaño n proveniente de una
distribución con función de densidad conocida f(x; q), y sea T =u(X1, X2,
…, Xn) cualquier estadístico. Queremos encontrar una función u
que proporcione la “mejor” estimación de q.
Se define el error cuadrático
medio:
ECM
(T) =E [(T- q)2]
Por tanto, se tiene:
ECM (T) = E[(T2-2Tq + q2)]=E
(T2) –2qE(T) + q2=(E
(T2) –E(T)2) + E(T)2-2qE(T) + q2
= Var (T) + [E(T) - q]2= Var (T) + [q-E(T)]2
El error cuadrático medio es la suma de dos cantidades positivas, una es la
varianza del estimador y la otra el cuadrado del sesgo del estimador.
Visto de una manera simple, el “mejor” estimador será aquel que
minimice el ECM. Sin embargo, aún en el caso en el que determinemos el ECM para
un gran número de estimadores, para la mayor parte de las funciones de densidad
f(x; q) no existe un estimador que minimice el error cuadrático medio para todos
los posibles valores de q. Por esta razón hay que añadir
criterios adicionales para la selección de los estimadores de q.
En el ECM el término [q-E(T)] recibe el nombre de sesgo
del estimador.
Se dice que T=u(X1, X2, …, Xn) es un
estimador insesgado del parámetro q, si E(T)=
q para cualquier q.
De esta forma, para cualquier estimador insesgado de q,
la distribución de muestreo de T se encuentra centrada alrededor de q
y ECM(T)=var(T).
Puede demostrarse que si:
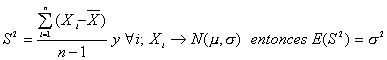
Demostración

Como Y sigue una Chi-cuadrado con n-1 grado de libertad; E(Y) = n-1. Luego
![]()
Este resultado se puede extender sin importar cuál sea la distribución de probabilidad de la población de interés.
Sea X1, X2, …, Xn una muestra aleatoria de alguna población con función de densidad no especificada de manera que E(Xi)=m y Var(Xi)=s2 para todo i. Entonces si
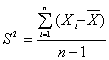
S2 es un estimador insesgado de s2, es decir sólo cuando se divide por n-1, se obtiene un estimador insesgado.
Estimadores consistentes.
La idea es que conforme se va aumentando el tamaño de la muestra, el estimador se va concentrando cada vez mas alrededor de q.
Sea T un estimador del parámetro q, y sean T1, T2, …, Tn una secuencia de estimadores que representan a T en base a muestras de tamaño 1, 2, …, n; respectivamente. Se dice que T es un estimador consistente de q si:
![]()
El requisito
![]()
constituye lo que se llama convergencia en probabilidad.
Esto implica que la varianza de un estimador consistente Tn disminuye conforme n crece. Una condición necesaria, aunque no suficiente para que Tn sea un estimador consistente de q es que Var(Tn) tienda a cero cuando n tiende a infinito.
Por ejemplo: la media muestral y la varianza muestral son estimadores consistentes de m y s2. para demostrarlo veamos primero el importante teorema siguiente:
Sea X una variable aleatoria con función de densidad f(x) y tal que E(X)=m y Var(X)=s2 son finitas. Entonces:
![]()
o de otra manera
![]()
Sean X1, X2, …, Xn n variables aleatorias IID, tales que E(Xi)=m y Var(Xi)=s2 y son finitas. Entonces

es un estimador consistente de m. Es decir:
![]()
Este importante teorema se conoce con el nombre de Ley de los grandes números
Demostración
Dado que E( X n)=m y Var( X n )=s2 / n, aplicando la desigualdad de Tchebycheff, se tiene:
![]()
Tomando
![]()
se tiene :
![]()
Tomando
límites cuando n tiende a ¥.
![]()
y por tanto:
![]()
Considérese una muestra de tamaño n de una distribución que tiene varianza conocida s2=10 y media desconocida m. ¿Cuál debe ser el tamaño de la muestra para que la media
![]() se encuentre dentro de un intervalo igual a 2 unidades de la media poblacional
con una probabilidad de al menos 0,9?.
se encuentre dentro de un intervalo igual a 2 unidades de la media poblacional
con una probabilidad de al menos 0,9?.
![]()
Por tanto:
![]()
De otro lado
![]()
Para un parámetro dado q, considérese la clase formada por todos los estimadores insesgados de q. Si T es un estadístico perteneciente a esta clase, entonces E(T)=q y ECM(T) = Var (T). Debe buscarse una clase de estimadores insesgados, si es que existe, que tenga una varianza mínima para todos los valores de q. Este estimador recibe el nombre de estimador insesgado de varianza mínima uniforme (VMU) de q.
Sea X1, X2, …, Xn una muestra aleatoria cuya función de probabilidad es f(x; q). Sea el estadítico T=u(X1, X2, …, Xn) un estimador de q tal que E(T)=q y Var(T) es menor que la varianza de cualquier otro estimador insesgado de q. Se dice que T es un estimador insesgado de varianza mínima.
Si T1 y T2 son dos estimadores insesgados de q, T1 es más eficiente que T2 si Var(T1)£Var(T2) cumpliéndose la desigualdad en sentido estricto para algún valor de q.
S muy común utilizar el cociente Var(T1)/Var(T2) para medir la eficiencia. La búsqueda de un estimador VMU se facilita bastante con la ayuda de un resultado que recibe el nombre de cota inferior de Cramer-Rao.
Sea X1, X2, …, Xn una muestra aleatoria de función de densidad de probabilidad f(x;q). Si T es un estimador insesgado de q, entonces la varianza de T debe de satisfacer la siguiente desigualdad.
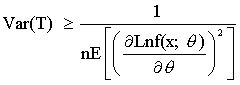
Si T es cualquier estimador insesgado del parámetro q tal que
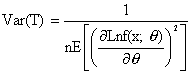
Entonces T es un estimador eficiente de q.
Intuitivamente, un estadístico es suficiente para el parámetro q si utiliza toda la información contenida en la muestra aleatoria con respecto a q.
Un criterio para ver si un estadístico es suficiente viene dado por el teorema de factorización de Neyman.
Sea X1, X2, …, Xn una muestra de una distribución con una función de densidad de probabilidad f(x;q). Se dice que T=u(X1, X2, …, Xn) es un estadístico suficiente de q si y solo si la función de verosimilitud puede factorizarse de la siguiente forma:
L(x1, x2, …, xn)=h(t;q)g(x1, x2, …, xn)
Para cualquier valor t=u(x1, x2, …, xn) de T y en donde g(x1, x2, …, xn) no contiene al parámetro q.
¿Cómo obtener estimadores que cumplan con las propiedades deseables de los estimadores?. Veamos el método de máxima verosimilitud y el de los momentos. Más adelante, en otro capítulo, se estudiará el método de mínimos cuadrados:
En esencia el método consiste en seleccionar como estimador a aquél valor del parámetro que tiene la propiedad de maximizar el valor de la probabilidad de la muestra observada. Es decir, encontrar el valor del parámetro que maximiza la función de verosimilitud.
Sea X1, X2, …, Xn una muestra aleatoria de una distribución con función de densidad de probabilidad f(x; q), y sea L(x1, x2, …, xn;q) la verosimilitud de la muestra como función de q. Si t=u(x1, x2, …, xn) es el valor de q para el cual la función de verosimilitud es máxima, entonces T=u(X1, X2, …, Xn) es el estimador de máxima verosimilitud de q.
El método de máxima verosimilitud proporciona el estimador eficiente, si es que existe. Sin embargo, los estimadores de MV son por lo general sesgados.
Por otra parte, es más fácil, generalmente, maximizar Ln(L(q)) que L(q).
El método de máxima verosimilitud posee otra propiedad deseable conocida como propiedad de invarianza.
![]()
el estimador de máxima verosimilitud de q. Si g(q) es una función univaluada de q, entonces el estimador de máxima verosimilitud de g(q) es g(q^).
Este método consiste en igualar los momentos apropiados de la distribución de la población con los correspondientes momentos muestrales para estimar un parámetro desconocido de la población.
Sea X1, X2, …, Xn una muestra aleatoria con función de densidad f(x;q). El r-ésimo momento alrededor de cero se define como
![]()
El método de los momentos constituye una alternativa razonable cuando no pueden hallarse los estimadores de máxima verosimilitud.
Téngase en cuenta que muchas veces los parámetros son funciones de los momentos teóricos.
Una prueba típica de duración consiste en seleccionar de manera aleatoria un conjunto de artículos iguales y someterlos a un cuidados proceso hasta que el articulo falla.
Si la prueba de duración se termina sólo cuando todos los articulos han fallado, se dice que la muestra aleatoria de tiempos está completa. Sin embargo, generalmente, si la prueba termina después de un lapso determinado de tiempo x0 o después de la falla de un número determinado de unidades m £n. Las dos condiciones producen muestras censuradas.
Si X0 es un lapso fijo de tiempo, el número de unidades que fallan de las n, después del comienzo de la prueba hasta el tiempo x0, es una variable aleatoria, se dice entonces que la muestra es del tipo I
Si m es fijo y el tiempo de terminación es la variable aleatoria Xm, se dice que la muestra es de tipo II.
Si no se tienen en cuenta las inferencias, existe muy poca diferencia entre ambos tipos.
Estudiemos las de tipo II.
Supongamos que el primer fallo se dio
en un tiempo igual a x1 desde el comienzo y el 2º en un tiempo x2,
también desde el comienzo, y así hasta xm, en donde m £n, es el número fijado de
antemano para terminar la prueba. Es obvio que x1£
x2 £ ... £ xm
y que n-m unidades tienen un tiempo de supervivencia xm.
Supóngase que los tiempos de duración son variables aleatorias X1, X2, …, Xn independientes normalmente distribuidas, con función de densidad
![]()
El interés recae en encontrar el estimador de máxima verosimilitud de q.
La
función de verosimilitud para un muestreo censurado del tipo II es la
probabilidad de que fallen m unidades en los tiempos x1,
x2 ,
..., xm es f(x1;q).f(x2;q)…f(xm;q). Pero ésta es una de las formas en las que pueden fallar m unidades de n.
El número total de formas es:
![]()
La probabilidad de que n-m unidades sobrevivan un tiempo xm está por la función de confiabilidad a tiempo xm.
![]()
Por tanto la función de verosimilitud es

Siendo
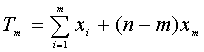
Tomando logaritmos
![]()
Derivando con respecto a q.
![]()
Se deduce que
![]()
Luego