
 |
Para volver al menú principal pulse sobre la palabra |
|---|
1. Experimentos estadísticos
2. Diseños estadísticos.
3. Análisis de experimentos unifactoriales en un diseño completamente aleatorio
4. Análisis de la varianza para un modelo de efectos fijos
5. Método de Schaffé para comparaciones múltiples.
6. Análisis de residuos
7. El caso de efectos aleatorios
8. El caso de efectos aleatorios
9. Análisis de experimentos con un solo factor en un diseño en bloque completamente aleatorizado.
10. Experimentos factoriales
Supóngase que se desea identificar el comportamiento de un sistema con respecto a su funcionamiento y costo en distintas condiciones; entonces debe pensarse en un experimento como medio para que el sistema sea observado bajo las condiciones de interés, de tal manera que su comportamiento pueda conocerse.
La parte más importante de un experimento es su formulación. Una vez definido, es necesario identificar la variable para medir o respuesta y el factor o factores potenciales que puedan influenciar la variabilidad de la respuesta. La respuesta se conoce también como variable dependiente, los factores reciben el nombre de variables independientes: se supone que estos últimos se encuentran bajo control del investigador.
Un nivel de tratamiento del factor es un valor o condición de este bajo el cuál se observará la respuesta medible.
Una unidad experimental se define como el objeto (persona o cosa) que es capaz de producir una medición de la variable de respuesta después de aplicar un tratamiento dado.
No siempre puede asegurarse el control de los factores externos. Tal desviación del control ideal necesita de la repetición del experimento en una muestra de unidades experimentales que permitan determinar la variación aleatoria o error experimental.
Esta es la variación que no puede atribuirse a un cambio en el tratamiento. Por ejemplo, puede ser interesante el efecto del aumento de las tasas de interés (tratamiento) en la actividad de la construcción de casas (respuesta) por parte de los constructores (unidades experimentales). Los tratamientos no pueden aplicarse a las unidades experimentales, ni la respuesta puede medirse de acuerdo con un experimento planeado.
El proceso por medio del cual se miden las observaciones de las respuestas se centra en el diseño estadístico. En general, en los experimentos diseñados estadísticamente, las unidades experimentales deben seleccionarse en forma imparcial, así como los tratamientos aplicados a estas, mediante un proceso aleatorio, con el propósito de remover los posibles sesgos sistemáticos.
Es de especial importancia el concepto de repetición. El propósito es medir el error experimental.
El interés recae también en como asignar las unidades experimentales a los tratamientos (o viceversa), para asegurar un proceso imparcial.
En este contexto surgen dos conceptos básicos: la asignación debe hacerse con base en un diseño completamente aleatorio, o en un diseño en bloques completamente aleatorio.
En forma general se hace uso de un procedimiento aleatorio sencillo como la generación de números aleatorios para llevar a cabo el proceso de asignación. En este modelo está implícito que las condiciones bajo las cuales será observada la respuesta serán las mismas a lo largo de todo el experimento.
A veces el investigador observa que el experimento no se puede conducir en el mismo ambiente, debido principalmente a que no todas las unidades experimentales son homogéneas; por lo tanto éstas hay que clasificarlas en bloques homogéneos y se asignan todos los tratamientos de forma aleatoria a las unidades de cada bloque.
La razón de agrupar en bloques es tomar en cuenta, y de esta forma remover, la fuente de variación en la respuesta que no es de interés, con lo que se incrementa la sensibilidad para detectar diferencias entre los tratamientos.
El más sencillo es aquel que compara el efecto de k≥2 niveles de un solo factor sobre alguna variable de respuesta.
Los niveles del factor son los tratamientos, y si estos se aplican de forma aleatoria a un conjunto virtualmente homogéneo de unidades experimentales, el experimento tiene un diseño completamente aleatorio.
Esta situación es la extensión natural del problema que surge cuando se comparan dos medias poblacionales cuando las varianzas son desconocidas pero iguales.
Para k≥2 niveles, se desea probar la hipótesis nula.
![]()
contra la alternativa de que alguna de las medias de la población no son las mismas.
Si es posible rechazar la hipótesis nula con base en k muestras independientes, entonces las medias de las k poblaciones no son todas iguales entre sí, o el efecto de los tratamientos sobre la respuesta es estadísticamente discernible. Si no puede rechazarse la hipótesis nula, cualquier desviación observada en la respuesta se debe solo al error aleatorio y no a causa de un cambio en el tratamiento.
La técnica del análisis de la varianza proporciona el procedimiento inferencial para probar la hipótesis nula. Para desarrollar esta técnica, se analizará el siguiente problema; saber si tiene algún efecto sobre el consumo de energía ligeras diferencias en el aislamiento de los techos de las casas. Supóngase que se tiene interés en k diferentes niveles de aislamiento en el techo, tales que para el j-ésimo nivel se observará el consumo de energía mensual del sistema de calentamiento en nj casas diferentes pero muy similares. Las casas se seleccionan homogéneas y los factores externos están controlados dentro de ciertos límites prácticos. La respuesta medible es el número de Kilowatios-hora mensuales.
|
1 |
2 |
|
j |
|
k |
|
Y11 |
Y12 |
.
. . |
Y1j |
.
. . |
Y1k |
|
Y21 |
Y22 |
.
. . |
Y2j |
.
. . |
Y2k |
|
|
|
.
. . |
|
.
. . |
|
|
Yi1 |
Yi2 |
.
. . |
Yij |
.
. . |
Yik |
|
|
|
.
. . |
|
.
. . |
|
|
Yn1
1 |
Yn2
2 |
.
. . |
Ynj
j |
.
. . |
Ynk
k |
Se supone que cada nivel de aislamiento térmico en los techos representa una población a partir de la cual se obtiene una muestra; también, que las distribuciones de las poblaciones para cada nivel de aislamiento son normales con varianzas iguales. Si la hipótesis nula es cierta, la observación Yij es el uso promedio de la energía de los sistemas de calentamiento para todos los k niveles de aislamiento térmico y cualquier desviación promedio se debe a un error aleatorio. Si H0 es falsa, entonces Yij está constituida por todos los promedios más el efecto del j-ésimo tratamiento y el error aleatorio.
El modelo matemático para un experimento unifactorial completamente aleatorio es:
![]()
Donde j=1, 2, …, k y i=1, 2, …, nj.
m es la media sobre las k poblaciones
τj es el efecto de respuesta debido al j-ésimo tratamiento
εij es el error experimental para la i-ésima observación bajo el j-ésimo tratamiento.
Se supone que los errores son independientes y están normalmente distribuidos con medias cero y varianzas iguales. Es decir,
![]()
La suposición sobre τj depende de cómo considere el investigador los niveles del factor. Si está interesado en lo que le pasa a la respuesta, sólo para ciertos niveles del factor que se seleccionan de antemano, entonces τ1, τ2 … τk se consideran parámetros fijos tales que:
![]()
Este modelo se conoce como de efectos fijos.
Si los niveles se seleccionan al azar, de una población de posibles niveles, entonces τ1, τ2 … τk son variables aleatorias tales que
![]()
y el modelo se conoce como de efectos aleatorios.
Para un modelo de efectos fijos, la hipótesis nula es
![]()
que establece que no existe ningún efecto de los tratamientos sobre la respuesta, lo que a su vez implica que las k medias de la población son iguales entre sí. Entonces se tiene que cada observación consiste en una media común y cualquier desviación con respecto a ésta se debe a la variación inherente dentro de cada población.
Para un modelo de efectos aleatorios la hipótesis nula consiste en la proposición de que la varianza entre las tj ( o los efectos de los tratamientos ) es cero. Es decir,
![]()
Así, al suponer independencia entre los errores y tratamientos aleatorios
![]()
El interés recae en hacer una evaluación de cuánto de la varianza de las observaciones se debe a diferencias reales entre las medias.
Sean m1, m2, ..., mk las medias de k poblaciones, y sea m la media de todas las poblaciones. Se define tj como: tj = mj-m. eij = Yij-mj. En estas condiciones el modelo de efectos fijos puede ponerse como
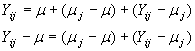
Esta última igualdad establece que cualquier desviación de una observación con respecto a la media global se debe a dos posibles causas: A la diferencia en el tratamiento o a un error aleatorio.
Si se rechaza la hipótesis nula H0: tj=0, los datos de la muestra deben de demostrar que la desviación total que se debe a los tratamientos es, suficientemente más grande, que la que se debe al error aleatorio.
Los parámetros m1, m2, …, mk y m son desconocidos, pero pueden estimarse con base en las observaciones de k muestra aleatorias.
Para la tabla anterior se define:
Al sustituir
se obtiene:
![]()
Donde se ha descompuesto la desviación de una observación con respecto a la media total de la muestra en dos componentes, la desviación de la media del tratamiento con respecto a la media total y la desviación de la observación con respecto a la media del tratamiento.
Para determinar un estadístico de prueba, elevando al cuadrado y sumando para todo i,j; se tiene:
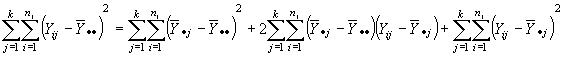
El doble producto vale 0. Quedando pues la formula reducida a
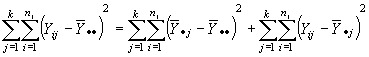
El término de la izquierda STC es la suma total de cuadrados.
El siguiente término es SCTR la suma de cuadrados de los tratamientos.
Y el último término es SCE la suma de cuadrados de los errores.
La expresión anterior se reduce a
STC
= SCTR + SCE
SCE mide la cantidad de variación de las observaciones debidas a un error aleatorio.
Puede demostrarse que bajo la hipótesis nula (H0: tj = 0. ) y bajo la suposición de que eij sigue una normal N(0; s2) entonces:
SCTR/s2 y SCE/s2 son 2 variables aleatorias independientes con una distribución chi-cuadrada, y por tanto STC/s2 también sigue una chi-cuadrado.
Como STC tiene N-1 grado de libertad, pues la suma de las desviaciones
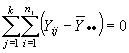
Y SCTR tiene k-1 grado de libertad, pues
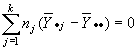
Esta restricción surge del hecho de que
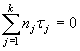
Por tanto, se tiene que SCE tendrá (N-1)-(k-1) = (N-k) grados de libertad. Luego, resumiendo:
![]()
![]()
Por tanto
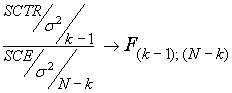
Este cociente es el estadístico apropiado para probar la hipótesis nula H0: tj = 0.
Esto puede verificarse de la siguiente forma: Si definimos al cuadrado medio de los tratamientos como
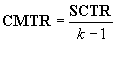
y el cuadrado medio de los errores
![]()
puede demostrarse que
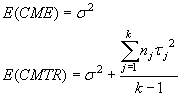
donde s2 es la varianza común de los errores.
Si H0 es cierta, entonces tj = 0 para cualquier j por tanto
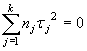
luego, E(CMTR)=s2. Es decir, tanto CME como CMTR son dos estimadores insesgados de s2. Pero si H0 no es cierta, CMTR > CME dado que el sumando anterior es siempre positivo. En otras palabras, cuanto mayor sea la diferencia entre las medias de los tratamientos y la media global, mayor será CMTR. Pero una ocurrencia de este tipo sugiere que las medias de los k tratamientos no son todas iguales. En consecuencia, la hipótesis nula será rechazada si
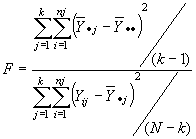
se encuentra dentro de una región crítica superior de tamaño a.
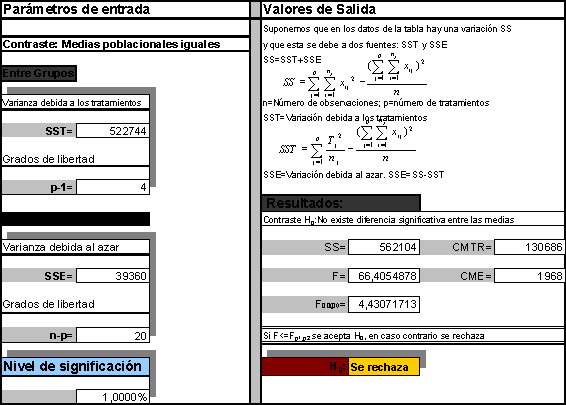
El análisis anterior constituye la técnica del análisis de la varianza para un experimento con un solo factor completamente aleatorizado. Todo ello se resume en la Tabla ANOVA.
![]()
Recuérdese que la hipótesis alternativa no indica qué medias son diferentes. El método de Scheffé radica en la formulación de un contraste que es una comparación que escoge el investigador para representar una combinación lineal de cualquier número de medias de la población.
Se define un contraste, denotado por L, como

en donde mj es la media del j-ésimo nivel, y las cj son constantes tales que:
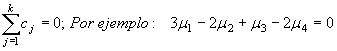
Un estimador no sesgado de L está dado por
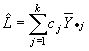
cuya varianza se estima mediante
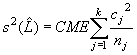
Scheffé demostró que todos los posibles contrastes definidos por (*) se encuentran incluidos, con una probabilidad 1-a, en el conjunto de intervalos
![]()
en donde
![]()
Si para algún L se obtiene un intervalo que no contiene al 0, entonces el contraste es estadísticamente discernible. En realidad para cada contraste L se está probando la hipótesis nula
![]()
Para muestras de tamaño diferente, el efecto de violar la suposición de varianzas iguales cuando se comparan dos medias puede ser sustancial. Dado que esta misma suposición se formula cuando se contrasta k medias, veamos como puede detectarse la violación de estos supuestos.
Un residuo es un estimador del error aleatorio eij. Dado que
![]()
el residuo correspondiente, denotado por eij, se define por
![]()
Los residuos no son estimados en el sentido de estimación de parámetros, sino como estimadores de las variables aleatorias no observables eij con base en las medias muestrales
![]()
Si es cierta la suposición de que los errores aleatorios tienen la misma varianza para los k niveles de población, entonces la gráfica de los residuos para cada tratamiento no revelará ninguna diferencia apreciable de los residuos alrededor de cero.
Para normalizar la escala de magnitudes es preferible utilizar los residuos estandarizados
![]()
Entonces, dado que los errores aleatorios se encuentran normalmente distribuidos, un residuo estandarizado rara vez se encuentra mas allá de ±3.
También se encuentra en la literatura estadística procedimientos para verificar la hipótesis de igualdad entre las k varianzas. Por ejemplo las pruebas de Bartlett y las pruebas de Hartley.
En el análisis de la varianza, la estadística F también es más robusta entre varianzas desiguales siempre y cuando los tamaños de la muestra de los tratamientos sean iguales. Esto para el caso de efectos fijos.
El resultado no se extiende para el caso de efectos aleatorios en el que la violación de la hipótesis de varianzas iguales generalmente tendrá efectos considerables sobre las inferencias aún para muestras del mismo tamaño. La hipótesis crucial en el desarrollo del análisis de la varianza es que los errores aleatorios sean independientes. Si los errores son interdependientes, el tamaño real de la región crítica puede ser, en forma sustancial, más grande (5 ó 6 veces) que el tamaño dictado al seleccionar la probabilidad de tipo I.
Para el caso de efectos aleatorios se formuló la suposición de que los niveles empleados en el experimento fueran seleccionados en forma aleatoria de una población de posibles niveles. Además se supondrá que
![]()
en donde st2 es la varianza de los tratamientos tj. La descomposición en suma de cuadrados y del análisis de la varianza es igual a la del caso de efectos fijos para un experimento con un solo factor, pero en este caso el valor esperado del cuadrado medio del tratamiento es diferente.
Dadas muestras del mismo tamaño, n, para todos los niveles, se puede demostrar que
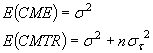
La región apropiada de rechazo sigue siendo la misma ya que un valor grande del cociente entre CMTR y CME sugiere que debe rechazarse la hipótesis nula H0: st2 = 0.
En el análisis de la varianza, la estadística F también es más robusta entre varianzas desiguales siempre y cuando los tamaños de la muestra de los tratamientos sean iguales. Esto para el caso de efectos fijos.
El resultado no se extiende para el caso de efectos aleatorios en el que la violación de la hipótesis de varianzas iguales generalmente tendrá efectos considerables sobre las inferencias aún para muestras del mismo tamaño. La hipótesis crucial en el desarrollo del análisis de la varianza es que los errores aleatorios sean independientes. Si los errores son interdependientes, el tamaño real de la región crítica puede ser, en forma sustancial, más grande (5 ó 6 veces) que el tamaño dictado al seleccionar la probabilidad de tipo I.
Para el caso de efectos aleatorios se formuló la suposición de que los niveles empleados en el experimento fueran seleccionados en forma aleatoria de una población de posibles niveles. Además se supondrá que
![]()
en donde st2 es la varianza de los tratamientos tj. La descomposición en suma de cuadrados y del análisis de la varianza es igual a la del caso de efectos fijos para un experimento con un solo factor, pero en este caso el valor esperado del cuadrado medio del tratamiento es diferente.
Dadas muestras del mismo tamaño, n, para todos los niveles, se puede demostrar que
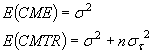
La región apropiada de rechazo sigue siendo la misma ya que un valor grande del cociente entre CMTR y CME sugiere que debe rechazarse la hipótesis nula H0: st2 = 0.
Recuérdese que cuando las unidades experimentales no son homogéneas se introduce una función potencial de variación que, en general, puede afectar a la inferencia con respecto al factor de interés. En estos casos es necesario emplear un diseño aleatorizado para remover la fuente externa de variación con lo que se incrementa la sensibilidad para detectar diferencias entre los tratamientos de interés. Las observaciones del experimento pueden colocarse como se observa en la tabla.
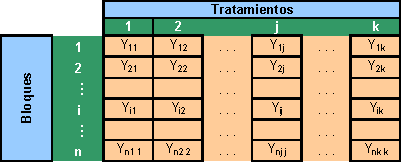
El modelo matemático para el diseño de un solo factor en bloque completamente aleatorizado es
![]()
Donde i = 1, 2, …, n y j = 1, 2, …, k. e Yij es la observación de la respuesta en el i-ésimo bloque y bajo el j-ésimo tratamiento, m es la media global, bi es el efecto sobre la respuesta debido al i-ésimo bloque, tj es el efecto debido al j-ésimo tratamiento y eij es el error aleatorio. Se supone que los eij son variables aleatorias independientes y normales N (0, s2) para cualquier i, j.
Si tanto los tratamientos como los bloques son de efectos fijos, entonces los bi* y los tj* son parámetros fijos que representan desviaciones de las medias de los bloques y los tratamientos de la media global, respectivamente. En otras palabras:
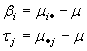
en donde
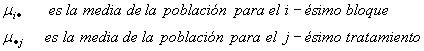
Al igual que en el diseño completamente aleatorizado, se supone que las varianzas de la población para todos los tratamientos son iguales. También se supone que el efecto del tratamiento sobre la respuesta es el mismo para todos los bloques.
Cuando esto ocurre se dice que los tratamientos y los bloques no interactúan y sus efectos son aditivos.
Para un diseño de un solo factor en un bloque completamente aleatorizado, el principal propósito es determinar si las diferencias en los tratamientos son estadísticamente significativas, es decir, para el caso de efectos fijos se desea probar la hipótesis nula
H0: tj =0.
El efecto bloque, en sí, no presenta interés y en realidad éste recae en aislar el efecto bloque y removerlo del error experimental, de manera que se incremente la eficiencia en detectar diferencias reales entre los tratamientos, si es que éstas existen.
Para el procedimiento del análisis de la varianza
![]()
Sustituyendo para bi y tj se obtiene:
![]()
![]()
y llevando estos valores a la expresión (1)
![]()
En otras palabras, la desviación de una observación con respecto a la media global tiene 3 componentes: uno debido a los bloques; otro, a los tratamientos y por último al error aleatorio. De la tabla anterior se obtiene:
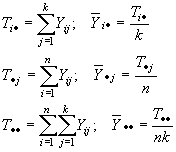
Por tanto, la igualdad anterior en términos de la muestra se expresa:
![]()
Al elevar al cuadrado ambos miembros y llevar la suma sobre i, j se tiene la relación.
![]()
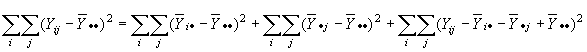
en donde puede demostrarse que los tres términos cruzados se reducen a cero.
Esto nos lleva a la ecuación fundamental para el análisis de la varianza
STC =
SCB + SCTR + SCE
Por causa de la restricción
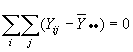
el número de grados de libertad es nk-1. de forma similar, por causa de las restricciones
![]()
el número de grados de libertad de SCB y de SCTR es de n-1 y k-1, respectivamente. Se sigue que:
g.l
(SCE)= g.l (STC) – g.l (SCB) – g.l (SCTR)
g.l(SCE)=nk-1-(n-1)-(k-1)=nk-n-k+1=n(k-1)-(k-1)=(n-1)(k-1)
Puede demostrarse que bajo las suposiciones del modelo y la hipótesis nula H0: tj = 0; los cocientes SCTR/s2 y SCE/s2 son dos variables aleatorias independientes con una distribución de probabilidad chi-cuadrado con (k-1) y (n-1)(k-1) grado de libertad. También puede demostrarse que los valores esperados de los cuadrados medios del error y los tratamientos son:
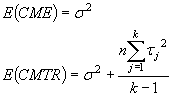
Entonces, con base en este argumento, el estadístico de prueba apropiado es el cociente de los cuadrados medios del tratamiento y del error, el cuál tiene una distribución F con k-1 y (n-1)(k-1) grados de libertad. Como antes, se sugiere una región crítica de tamaño a, ya que un valor grande del cociente tiende a indicar que no todas las medias de los tratamientos son idénticas. Debe notarse que es posible una prueba para el efecto de bloque al formar el cociente CMB y CME y compararlo con la región crítica que se encuentra en el extremo superior de la distribución F con (n-1) y (n-1)(k-1) g.l. El análisis de la varianza aparece en:

Al igual que se hizo con el método Schaffé pueden definirse y probarse un gran número de contrastes para probar si son estadísticamente discernibles. La única diferencia es que la cantidad denotada por A está ahora dada por:
![]()
A veces los bloques no son de efectos fijos, es decir se eligen para el experimento de forma aleatoria de una población de posibles bloques. Si los tratamientos son de efectos fijos, la única diferencia con respecto al caso previo se encuentra en la suposición de bi.
![]()
Pero el análisis sigue siendo el mismo; aún para comparaciones múltiples entre los tratamientos.
Además de la suposición de independencia, se hacen dos suposiciones claves para un diseño en bloques aleatorizado: las varianzas de cada tratamiento son iguales y los bloques y tratamientos no interactúan.
A veces es necesario investigar, en forma simultánea, los efectos que tienen varios factores sobre la respuesta. Una forma eficiente de lograr esto es mediante el uso de un experimento factorial en el que todos los niveles del factor se combinan con todos los niveles de cualquier otro para formar los tratamientos. Por ejemplo en un experimento factorial de 2 factores en el que uno tiene 3 niveles y el otro 2, existen 3x2=6 tratamientos. En otras palabras, la respuesta será observada bajo 6 tratamientos diferentes. Con los experimentos factoriales no sólo es posible evaluar los efectos individuales de los factores sobre la respuesta, sino que también es posible determinar el efecto causado por sus interacciones. El efecto de un factor sobre la respuesta es simplemente el cambio en esta, causado por los cambios en el nivel del factor. Pero si el efecto de un factor es diferente para distintos niveles de otro factor, entonces se dice que los dos factores interactúan entre sí. La presencia de interacción indica que el efecto de los factores sobre la respuesta no es lineal y de esta forma no puede asumirse un efecto aditivo.
En un experimento factorial que incluya 2 factores A y B con a y b niveles respectivamente, el número de tratamientos es igual a a.b. Si no se puede suponer un modelo aditivo (no interacción), sólo es posible una prueba para determinar si un efecto por interacción es estadísticamente apreciable, si se toma mas de una observación de la respuesta para cada tratamiento.
Si se suponen n aplicaciones de los ab tratamientos, el modelo matemático no aditivo para un factorial de dos factores es:
![]()
en donde Yijk es la k-ésima observación de la respuesta para el tratamiento (i, j); m es la media global, ai es ele efecto causado por el i-ésimo nivel de A, bj es el efecto causado por el j-ésimo nivel de B; y, (ab)ij es el efecto de la interacción para el i-ésimo nivel de A y el j-ésimo nivel de B y eijk es el error aleatorio en el tratamiento (i, j).
Como antes, se supone que las varianzas de la población para cada uno de los ab tratamientos son iguales, y que los errores aleatorios son variables aleatorias, normalmente distribuidas, con medias iguales a cero y varianza común s2. Si se supone que los factores A y B son de efectos fijos, entonces ai, bj, y (ab)ij son parámetros fijos tales que:
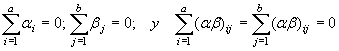
las siguientes hipótesis son de interés.
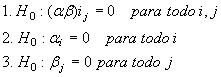
La dos últimas hipótesis incluyen los efectos (individuales) principales de los factores A y B, la primera hipótesis pertenece a la posible interacción entre A y B. Si existe una fuerte interacción entre A y B, los resultados de las pruebas para demostrar un efecto principal causado por A ó B pueden no ser significativos.
Podemos escribir el anterior modelo en términos de desviaciones
![]()
en donde
![]()
son, respectivamente, la media real del i-ésimo nivel de A; la media real del j-ésimo nivel de B; la media real del tratamiento (i, j).
Esta igualdad establece que la desviación de una observación con respecto al promedio global está formada por 4 componentes: las desviaciones causadas por el efecto principal de A; por el efecto principal B; por el efecto de la interacción entre A y B; por el error aleatorio.
Las observaciones pueden colocarse en el cuadro siguiente:
|
|
|
Factor
A |
||||
|
|
|
Nivel
1 |
|
Nivel
i |
|
Nivel
a |
|
Factor
B |
Nivel
1 |
Y111…Y11k…Y11n |
… |
Yi11…Yi1k…Yi1n |
… |
Ya11…Ya1k…Ya1n |
|
|
… |
… |
… |
… |
… |
|
|
Nivel
j |
Y121…Y12k…Y12n |
… |
Yi21…Yi2k…Yi2n |
… |
Ya21…Ya2k…Ya2n |
|
|
|
… |
… |
… |
… |
… |
|
|
Nivel
b |
Y1b1…Y1bk…Y1bn |
… |
Yib1…Yibk…Yibn |
… |
Yab1…Yabk…Yabn |
|
se definen las siguientes estadísticas
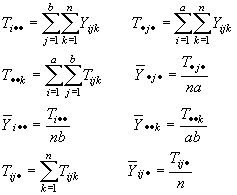
al reemplazar en el modelo los parámetros por sus estimadores se obtiene:
![]()
Si se elevan al cuadrado y se suman, sobre i, j, k todos los términos que tienen productos cruzados se reducen a cero, y se obtienen los siguientes resultados:
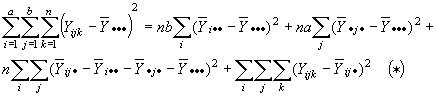
En otras palabras, la suma total de cuadrados se separa en la suma de cuadrados debidas: al factor A (SCA), al factor B (SCB), a la intersección de A y B (SCAB) y a los errores (SCE).
También puede escribirse el modelo en términos de las desviaciones causadas por los tratamientos y el error aleatorio, es decir:
![]()
En esta forma, la desviación debida a los tratamientos abarca los efectos debidos a A, B y la interacción AB. Al sustituir los correspondientes estadísticos se tiene:
![]()
al elevar al cuadrado y sumar en i, j, k.
![]()
STC
= SCTR + SCE
Comparando con la anterior, se deduce que:
SCTR
= SCA + SCB + SCAB
Puede demostrarse que, con base en (*) la descomposición del número de grados de libertad es la siguiente:
g.l (STC) = g.l (SCA) + g.l(SCB) + g.l(SCAB) + g.l(SCE)
(nab-1)=(a-1) + (b-1) + (a-1)(b-1) + ab(n-1)
Para las suposiciones del modelo y la hipótesis de interés
SCA/s2; SCB/s2; SCAB/s2 y SCE/s2 son variables aleatorias que se distribuyen según una chi-cuadrado con (a-1), (b-1). (a-1)(b-1) y ab(n-1) grados de libertad, respectivamente.
Por tanto la estadística de prueba para los efectos principales y de interacción son los cocientes entre los cuadrados medios correspondientes y el cuadrado medio del error, y tienen una distribución F.
Para el caso de efectos fijos, los valores esperados son:
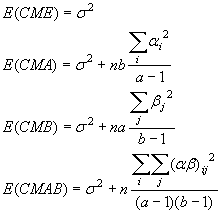
Si no existe ninguna interacción entre A y B (es decir, si (ab)ij=0 para todo i, j) entonces CMAB y CME tienen el mismo valor esperado y los efectos son aditivos.
Pero si el cociente CMAB/CME tiene un valor suficientemente grande, esto sugiere una interacción estadísticamente apreciable entre A y B y, por tanto, debe rechazarse la hipótesis nula. De manera similar, si ai = 0 para toda i, CMA y CME tiene valores esperados iguales y no existe un efecto principal atribuible a A. Pero un cociente grande entre CMA y CME tiende a implicar que el efecto principal atribuible a A es estadísticamente significativo.
El mismo argumento para B.
La tabla resumen del análisis de la varianza se muestra a continuación.
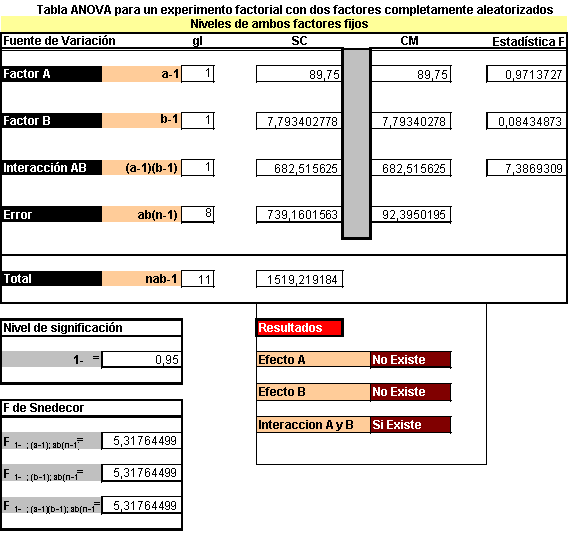
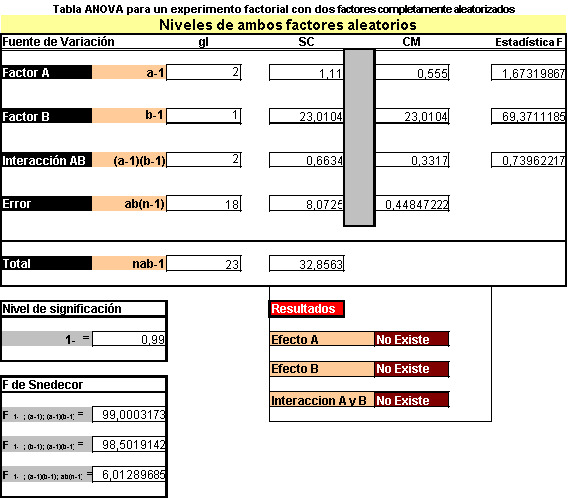

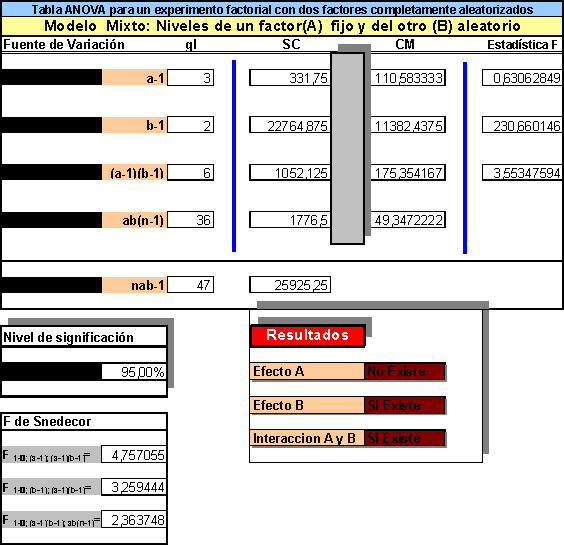
Debe notarse que el método de Scheffé para comparar las medias del nivel del factor se extiende, en forma directa, a experimentos factoriales.