
 |
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema
1. Distribución Uniforme
2. Distribución Binomial.
3. Distribución Polinomial
4. Distribución de Poisson
5. Distribución Hipergeométrica
6. Distribución geométrica o de Pascal
7. Distribución Binomial negativa.
Como se sabe, la ley de probabilidad de una variable aleatoria discreta X está bien definida si se conoce su distribución de probabilidad P(X=xi); i = 1, 2, …, n. O bien, si se conoce su función de distribución F(x), teniendo que:
![]()
Una variable aleatoria discreta X que toma valores enteros 1, 2, …, n con probabilidades: P(X=k)=1/n; k=1, 2, …, n recibe el nombre de variable uniforme discreta y su distribución de probabilidad distribución uniforme discreta.
a) Depende de un solo parámetro n.
b) Su media y varianza son:
![]()
Supongamos un experimento aleatorio S y consideremos asociado con él un suceso A de probabilidad p y sea A* el suceso contrario, cuya probabilidad será q=1-p. Para distinguirlos con mayor facilidad, al suceso A lo llamaremos éxito, y al suceso A* fracaso.
Repitamos el experimento en las mismas condiciones n veces y supongamos que:
a) El resultado de cada ensayo es independiente de los resultados anteriores.
b) La probabilidad de A permanece constante y no varía de una prueba a otra..
Todo experimento que tenga esta características diremos que
sigue el modelo de la distribución
binomial.
A la variable X que expresa el número de éxitos obtenidos en las n pruebas del experimento aleatorio la llamaremos variable aleatoria binomial. Representaremos por B(n, p) a la variable de la distribución, siendo n y p los parámetros.
La
variable aleatoria que expresa el número de éxitos en n pruebas, es una
variable aleatoria discreta cuyos valores varían de 0, 1, 2, …, n. Y las
probabilidades con que toman dichos valores se calculan de la siguiente forma:
![]()
a) Media:
![]()
b) Varianza:
![]()
En ella hay que observar:
c) Es simétrica si p=q. Si p<q asimetría a la derecha; si p>q, asimetría a la izquierda. Cuando n ® ¥ la distribución tiende a ser simétrica (distribución normal).
d) Los valores de P(X=k) están tabulados para valores de p comprendidos entre 0 y 0.5. Si p>0.5, hay que tener en cuenta que B(n, k, p) = B(n, n-k, q).
El problema del ajuste es el de buscar una distribución binomial que “mejor” se adapta a unos datos, es decir, se ha de calcular el valor del parámetro p para el cual las probabilidades binomiales obtenidas sean las mas cercanas posibles a los datos. El procedimiento que se sigue es igualar la media de la muestra a la media de la población, con lo que tenemos:
![]()
Con este valor de p se calculan las correspondientes probabilidades y se comprueba si el ajuste es bueno. Para medir la bondad del ajuste de una manera objetiva existen métodos matemáticos que se tratarán más adelante.
Es una generalización de la distribución binomial para el caso de que en cada prueba se consideren k sucesos excluyentes A1, A2, …, Ak con probabilidades respectivas p1, p2, …, pk siendo la suma de todas igual a la unidad.
Supongamos que se realizan sucesivamente n pruebas independientes de este tipo y consideremos las variables Xi = ”Número de veces que ocurre el suceso Ai en las n pruebas”.
A la variable k-dimensional (X1, X2, …, Xk) se le denomina variable polinomial o multinomial.
Para hallar su función de probabilidad P(X1=n1, X2=n2, …, Xk=nk) con
![]()
consideremos uno de sus sucesos favorables:
![]()
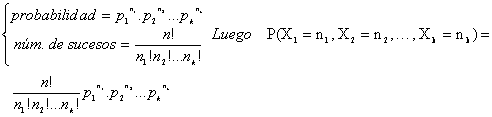
En ella hay que observar:
a) Depende de k parámetros n, p1, p2, …, pk-1.
b) Si el experimento consiste en extracciones de una urna, estas han de ser con reemplazamiento para mantener las probabilidades de los sucesos Ai constantes a lo largo de todas las pruebas.
Una variable aleatoria X sigue una distribución de Poisson si puede tomat valores enteros 0, 1, 2, …, n, …, con probabilidades:
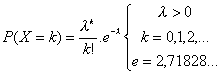
En esta distribución hay que observar:
a) Depende de un solo parámetro.
b) Su media, varianza son
![]()
c) Es una buena aproximación de la binomial cuando n grande y p pequeño:
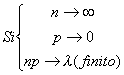
![]()
En general si n>50 y p<0.1 ó n.p<5 la distribución de Poisson es una buena aproximación de la Binomial.
d) La distribución de Poisson presenta una ligera asimetría hacia la izquierda. Cuando n tiende hacia infinito tiende a ser simétrica (distribución normal).
Consideremos una población de N elementos de dos clases A y A* excluyentes, de los cuales nA son de la clase A y nA* son de la Clase A*, con nA + nA* = N.
Al tomar un elemento de esta población la probabilidad de que proceda de una u otra clase es:

Sea ahora el experimento de tomar n elementos consecutivos de una población sin reemplazamiento. A la variable aleatoria X= “ número de elementos de la clase A en la muestra de tamaño n” se le denomina variable hipergeométrica.
Para hallar su función de probabilidad P(X=k) consideremos uno de los sucesos favorables:

Luego

En ella hay que observar
a) Depende de los parámetros N, n, p
b) Su media y varianza son:
![]()
c) Se diferencia de la binomial en que, en aquella las probabilidades son constantes a lo largo de las pruebas(extracciones con reemplazamiento) mientras que en la hipergeométrica, varían de una prueba a otra (extracciones sin reemplazamiento).
d) Si N es grande respecto de n, las probabilidades varían muy poco de una prueba a la siguiente, por lo que en estos casos se puede decir que la variable hipergeométrica sigue aproximadamente una distribución binomial, es decir:
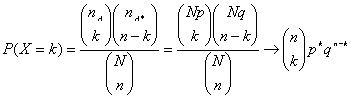
Se conviene en sustituirla cuando n/N<0.1
Por otra parte y de manera análoga a la distribución polinomial, si tenemos una población con N elementos repartidos en k clases excluyentes A1, A2, …, Ak con N1 elementos de la clase A1, N2 elementos de la clase A2, …, Nk elementos de la clase Ak siendo N1+N2+ …+ Nk = N, al tomar consecutivamente n elementos sin reemplazamiento y llamando Xi = “Número de elementos que hay de la clase Ai en la muestra de tamaño n” la variable k-dimensional (X1, X2, …, Xk) tiene por función de probabilidad:

Sea el
experimento consistente en la realización
sucesiva de pruebas de Bernoulli. A la variable X= “número de la
prueba en la que aparece por primera vez el suceso A” se le denomina variable
geométrica. Ara hallar la probabilidad de P(X=k), hay que notar que esta
probabilidad es la del suceso
![]() luego P(X=k)=qk-1.p
luego P(X=k)=qk-1.p
a) Esta distribución depende de un solo parámetro p.
b) Su media y varianza son
![]()
c) Si el experimento consiste en extracciones de una urna estas han de ser con reeemplazamiento.
Sea X = “número de pruebas en que aparece el suceso A* hasta la enésima aparición del suceso A”.
Para hallar la probabilidad del suceso P(X=k), consideremos uno de los sucesos favorables:
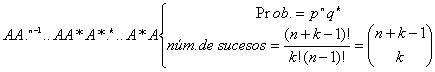
luego:
![]()
En ella hay que observar:
a) Depende de dos parámetros n y p.
b) Su media y varianza son:
![]()
c) Si el experimento consiste en extracciones de una urna, estas han de ser con reemplazamiento.