
 |
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema
1. Distribución Uniforme
2. Distribución Normal
3. Distribución Chi-cuadrado
4. Distribución t-Student
5. Distribución F de Fisher.
6. Distribución de Pareto.
7. Distribución Log-Normal
8. Distribución Beta
9. Distribución Gamma
10. Distribución de Erlang
11. Distribución de Weibull
12. Distribución exponencial negativa
Se dice que la variable aleatoria X sigue una distribución uniforma en el intervalo [a, b] cuando su función de densidad es
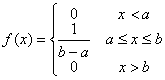
En esta distribución hay que observar que:
a) Depende de los parámetros a y b
b) Su función de distribución es
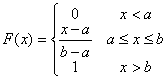
c) Su media y varianza son
![]()
La variable continua X se dice que sigue una distribución normal de media m y desviación típica s si:
a) Puede tomar cualquier valor en el intervalo (-¥; +¥)
b) Su función de densidad es:
![]()
la gráfica de esta función tiene forma de campana
En la distribución normal hay que observar:
c) Depende de dos parámetros m y s
d) Su función de distribución es igual a
![]()
e) Su media y varianza son m y s2
f)
La función de densidad presenta un máximo en x=m,
dos puntos de inflexión en x=m-s
y x=m+s
y tiene el eje OX como asíntota.
g)
La curva f(x) es simétrica respecto de x=m
y por tanto su media, mediana y moda coinciden. Esta propiedad es muy utilizada
en el cálculo de áreas mediante tablas.
h)
Si una variable X1 es N(μ1, σ1)
y otra variable X2 es N(μ2, σ2)
independientes entre sí, entonces la nueva variable aleatoria X=X1 ±
X2 sigue también su distribución normal de media μ1
± μ2 y desviación típica
![]() , es decir, la variable X sigue una
, es decir, la variable X sigue una
![]()
Esta
propiedad se generaliza a n variables.
i)
Si X es una N(μ, σ) la variable
![]()
su
función de densidad será
![]()
A la variable Z se le llama variable tipificada de X y a la curva de su función de densidad curva normal tipificada
En la distribución normal tipificada hay que observar que
j) No depende de ningún parámetro
k) Su media y varianza son 0 y 1.
l) La curva es simétrica respecto del eje z=0, tiene puntos de inflexión en z=-1 y z=1
Si X es una variable binomial de parámetros n y p, con n muy grande y con p y q no muy próximos a 0. Podemos considerar que la variable X sigue una distribución normal
![]()
y por tanto la variable
![]()
sigue una normal N(0, 1) para que esta transformación sea
correcta, hay que tener en cuenta que X es discreta y Z continua, por lo que P(X=a)=
al considerar que X es continua=
![]() y si tenemos en cuenta
y si tenemos en cuenta
![]()
En general la transformación es aceptable cuando (p<0.5 y np>5) ó (q<0.5 y nq>5)
La distribución de la variable Z se encuentra tabulada, en las tablas aparecen el área bajo la curva de la normal a la derecha de un punto Zα. Al punto Zα se le llama punto crítico y al área bajo la curva a la derecha del punto: α se le llama nivel de significación. Solo se encuentran valores de Zα mayores o iguales que 0 ó áreas α menores o iguales que 0.5. Los demás valores se obtiene por simetría.
La gran utilidad de la variable tipificada Z es que nos permita calcular áreas de cualquier variable con distribución normal.
Si X es N(μ, σ) entonces
![]()
Este proceso se denomina tipificación.
Sean X1, X2, …, Xn, n variables aleatorias N(0, 1) independientes entre sí. La variable
![]()
recibe el nombre de À2
de Pearson con n grados de libertad. Su función de densidad es
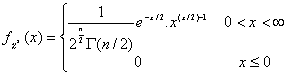
![]()
En esta distribución hay que observar:
a) Sólo puede tomar valores positivos por tratarse de una suma de cuadrados de n variables.
b) Depende sólo del parámetro n, por lo que no hay, como ocurría en la normal, una curva tipificada única
c) Su media y varianza son μ=n, σ2=2n
d) Si cn12 y cn2 2son dos distribuciones con n1 y n2 grados de libertad, independientes entre sí, entonces la suma de las dos es también una c2 con n1+n2 grados de libertad:
![]()
esta propiedad se puede generalizar a n variables.
e) Al aumentar el número de grados de libertad esta distribución se aproxima asintóticamente a la normal. Para n>30 la variable
![]()
f)
En el muestreo, si tomamos muestras de media
![]() y desviación típica s de una
población normal N(μ, σ), la variable
y desviación típica s de una
población normal N(μ, σ), la variable
![]()
con s2=cuasivarianza, es una c2 de Pearson con n-1 grados de libertad. Esta última propiedad es muy utilizada en la estimación y en el contraste de hipótesis sobre la varianza poblacional σ2.
g) Se encuentra la tabla de la c2 para valores de n<=30.
h) Para el uso de la tabla consideramos las áreas bajo la curva a la derecha de un punto c 2a;n crítico. A la derecha de este punto, el área bajo la curva es igual a α (nivel de significación) en una c 2de Pearson con n grados de libertad. Se tiene:
![]()
y para áreas a la izquierda
![]()
Sean X1, X2, …, Xn, X ; n +1 variables aleatorias N(0, σ) independientes entre sí. La variable tn:
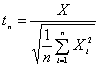
se denomina t de Student con n grados de libertad. Dividiendo en el segundo miembro numerador y denominador por σ, tenemos:
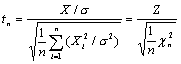
a) El campo de variabilidad de tn es toda la recta real.
b) Su distribución depende sólo del parámetro n.
c) Conforme n va aumentado, la curva que representa a la función de densidad va siendo cada vez mas apuntada, coincidiendo en el límite, cuando n ®¥ con la curva normal tipificada.
d) No depende de σ
e) Es simétrica respecto del eje de ordenadas OY.
f)
En el muestreo al tomar muestras de tamaño n de media
![]() y varianza s2 de una población N(μ, σ), la variable
y varianza s2 de una población N(μ, σ), la variable
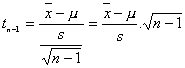
sigue una t de Student con n-1 grados de libertad. Esta propiedad es muy utilizada en la estimación y el contraste de hipótesis sobre la media de la población μ.
g) Está tabulada para diferentes valores de n. Para el uso de la tabla consideramos valores de ta,n (punto crítico) tales que el área bajo la curva a la derecha de este valor es igual a α (nivel de significación). Es decir:
![]()
sólo se encuentran valores de t ³ 0 ( o áreas α menores o iguales que 0.5). Para valores de t £ 0 se puede obtener por simetría.
Sean c12 y c22dos variables c2de Pearson con n1 y n2 grados de libertad, independientes entre sí. Entonces la variable:
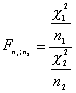
se le denomina F de Fisher_Snedecor con n1 y n2 grados de libertad. Tiene por función de densidad:
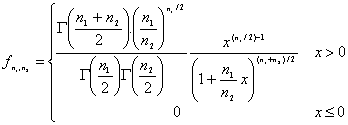
En esta distribución hay que observar :
a) El campo de variabilidad de la F es el intervalo (0, +¥ )
b) Depende de dos parámetros n1 y n2.
c) Es muy utilizada en análisis de la varianza.
d)
Se encuentra tabulada para diferentes valores de n1 y n2.
Para el uso de estas se consideran áreas a la derecha de un punto Fα;n1,n2
(punto crítico) que deja a la derecha, bajo la curva un área igual a α
(nivel de significación).
![]() .
.
En las tablas aparecen solo dos valores de α=0.05 y α=0.01. Para valores de α=0.95 y de α=0.99 se considera la relación:
![]()
Una variable aleatoria X sigue una distribución de Pareto de parámetros α y x0 si:
1. Puede tomar valores superiores o iguales a x0.
2. Su función de densidad es:
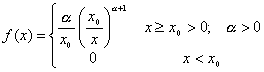
En esta distribución hay que observar que:
a) Depende de los parámetros α y x0.
b) Su función de distribución es:
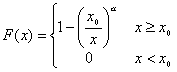
c) Su media y varianza para α >2 son:
![]() ;
;
![]() .
.
d) Es muy utilizada en economía, ya que la distribución de las rentas personales superiores a una cierta cantidad x0 sigue una distribución de Pareto de parámetros α y x0.
Se tiene

lo que nos permite determinar el número de personas que superan la renta x0. El parámetro α se determina a partir de la media muestral. Normalmente toma valores próximos a 2.
Una variable X sigue una distribución log-normal si los logaritmos neperianos de sus valores están normalmente distribuidos, es decir, si la variable Y=log X es N(m,s) es decir si:
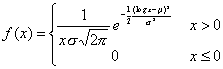
En ella observamos que:
a) Depende de los parámetros m y σ.
b) Su media y varianza son:
![]()
![]()
Se ha utilizado para representar variables físicas cuyos valores se encuentran restringidos a un intervalo de longitud finita y para encontrar ciertas cantidades que se conocen como límites de tolerancia sin necesidad de la hipótesis de una distribución normal. Además la distribución beta juega un gran papel en la estadística bayesiana.
La v.a X sigue una distribución beta si su función de densidad está dada por:

Es fácil ver que si se reemplaza x por 1-x se tiene:
f(1-x; b, a)=f(x; a, b).
Se define como:
![]()
Algunas propiedades de
esta función son:
a)
Si n es un entero positivo
![]()
![]()
![]()
La función beta se
define como:
![]()
Puede demostrarse que la función beta y la gamma se encuentran relacionadas por la expresión:
![]()
![]()
Supóngase que una pieza
está sometida a una cierta fuerza, de manera que se romperá después de
aplicar un número específico de ciclos fuerza. Si los ciclos ocurren de manera
independiente y a una frecuencia promedio dada, entonces el tiempo que debe
transcurrir antes de que el material se rompa es una variable aleatoria que
sigue una distribución gamma. Su función de densidad viene expresada por:
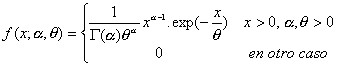
Esta distribución se emplea de manera extensa en una gran diversidad de áreas.
·
Para representar el tiempo de
falla de un sistema que falla solo si de manera exacta los componentes fallan y
la falla de cada componente ocurre a una frecuencia constante l=1/q
por unidad de tiempo.
·
En líneas de espera para
completar una reparación que se lleva a cabo en subestaciones; en cada una de
las cuales es un evento
independiente que ocurre a una frecuencia constante igual a
l=1/q.
·
Ingresos familiares.
·
Edad al contraer matrimonio.
![]()
La distribución gamma,
cuando a
es un entero positivo se conoce con el nombre de Erlang. Existe una asociación
entre los modelos de probabilidad de Poisson y de Erlang. Si el número de
eventos aleatorios independientes que ocurren en un lapso específico es una
variable aleatoria de Poisson con frecuencia constante de ocurrencia igual a 1/ q, entonces, para una a dada, el tiempo de espera hasta
que ocurre el a-ésimo
evento de Poisson sigue una distribución de Erlang.
Cuando a=1, la distribución de Erlang se reduce a una distribución
exponencial negativa. Nótese que la variable aleatoria de una
distribución exponencial negativa puede pensarse como el lapso que transcurre
hasta el primer evento de Poisson. De acuerdo con esto, la variable aleatoria de
Erlang es la suma de variables aleatorias independientes distribuidas
exponencialmente.
Otro caso especial del
modelo de probabilidad gamma es la distribución chi-cuadrado.
Si se hace a= u /2 y
q=2 , se
obtiene:
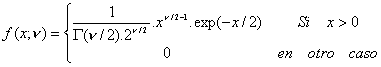
donde u recibe
el nombre de grados de libertad.
La media y varianza de la distribución chi-cuadrado se obtienen de los de
la gamma.
E[X]= u y
Var[X]=2. u
El esfuerzo al que se
someten los materiales puede modelarse por esta distribución. Se ha empleado
mucho en situaciones del tipo tiempo-falla con el objetivo de lograr una amplia
variedad de componentes mecánicos y eléctricos.
La función de densidad
está dada por:
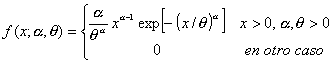
![]()
·
Si a=1 se reduce a la distribución exponencial negativa.
·
Cuando a=2 y q=Ö2 s.
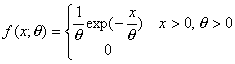
que
se conoce con el nombre de distribución de Rayleigh.
La distribución
exponencial negativa puede emplearse para modelar el lapso de tiempo entre dos
eventos consecutivos de Poisson que ocurren de manera independiente y a una
frecuencia constante. Esta distribución se emplea con bastante frecuencia con
objeto de modelar problemas del tipo tiempo-falla y como modelo para el
intervalo en problemas de líneas de espera. Se demuestra que esta distribución
no tiene “memoria”, en el sentido de que, la probabilidad de ocurrencia de
eventos presentes o futuros no depende de los que hayan ocurrido en el pasado.
De esta forma, la probabilidad de que una unidad falle en un lapso específico
de tiempo depende nada mas que de la duración de este, no del tiempo en que la
unidad ha estado en operación.
La función de densidad
está dada por:
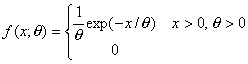
E[X]= q;
Var(X)= q2