
 |
Para volver al menú principal pulse sobre la palabra |
|---|
1. Introducción
2. Tablas de control estadístico
3. Tablas X¯ (media conocida de la población)
4. Tabla de S (desviación estándar conocida de la población)
5. Tablas ¯X y S (media y varianza desconocida de la población)
6. Procedimientos de muestreo para la observación
7. Desarrollo de planes de muestreo sencillo para riesgos estipulados del productor y del consumidor
8. Muestreo para la aceptación por variables.
Es necesario establecer un procedimiento para inspeccionar una muestra relativamente pequeña del producto proveniente de un lote para decidir si reúne los estándares de calidad deseados. Un procedimiento de este tipo incluye la noción de muestreo para la aceptación.
Es un proceso inferencial basado en un muestreo repetitivo. Se emplea para definir un estándar de calidad para un proceso de fabricación y para determinar si éste se mantiene durante el proceso. De esta forma una tabla de control estadístico de calidad es el proceso inferencial por el cual se decide si una desviación observada de la norma deseada se debe al azar o a alguna causa fija. Si es del azar se dice que el proceso está bajo control.
Los errores de tipo I y de tipo II se enuncian ahora de la manera siguiente: Error de tipo I, declarar a un proceso fuera de control cuando en realidad está bajo control. Error de tipo II: Declarar a un proceso bajo control cuando en realidad está fuera de control.
Sea X1, X2, …, Xn una muestra aleatoria de tamaño n, en donde cada
![]()
La probabilidad de que
![]()
Los límites de control tres-sigma son
![]()
Cuando se toma una muestra de tamaño n y se calcula la media muestral, si esta se encuentra en los límites anteriores se considera que el proceso se encuentra bajo control. Por lo tanto, cada vez que se toma una muestra se está probando la hipótesis nula de que la media del proceso es igual a μ contra la hipótesis alternativa, de que ha habido un corrimiento en la media del proceso.
Ejemplo 1
Una máquina rellena un recipiente con 500 g de una sustancia, con una desviación estándar de 2 g. Se toman 10 muestras diarias, cada una de 5 recipientes, y se mide el peso de cada recipiente. Los peso promedios para las 10 muestras en una semana son
|
Nº de muestra |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Media muestra |
498,37 |
499,49 |
501,25 |
498,63 |
502,97 |
500,56 |
499,23 |
498,76 |
501,05 |
500,27 |
Para los límites de control 3σ, ¿se encontró el proceso bajo control durante esta semana? Con estos límites, ¿cuál es la probabilidad de no detectar un corrimiento de 500 a 503 g en la media?
Dado que n=5, μ=500 y σ=2, los límites de control 3σ son 500±3 (2/50,5)=(497,3167; 502,5833). Nótese en la figura que la media muestral quinta está por encima del límite superior; de esta forma, durante este tiempo el proceso se juzgó como fuera de control.
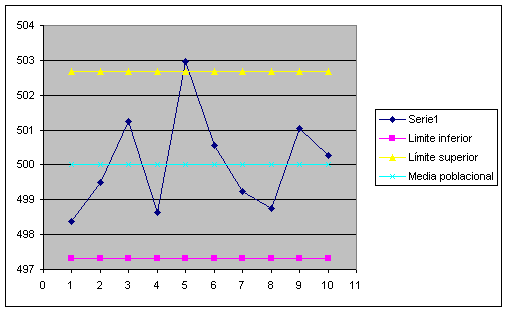
La probabilidad de obtener un valor de la media muestral fuera de los límites de control si el proceso se encuentra realmente bajo control es:
![]()
valor que se obtiene de 1-(DISTR.NORM(502,683282;500;2/5^0,5;VERDADERO)-DISTR.NORM(497,316718;500;2/5^0,5;VERDADERO))
Veamos el 2º apartado, la probabilidad de no detectar un corrimiento en la media cuando ésta pasa a μ=503 es igual a:
![]()
valor que se obtiene: =(DISTR.NORM(502,683282;503;2/5^0,5;VERDADERO)-DISTR.NORM(497,316718;503;2/5^0,5;VERDADERO))
La variabilidad de un proceso es casi tan importante como el control del promedio. Mantener un nivel aceptable en las tasas de variación se considera vital en la fabricación de instrumentos de precisión.
Las tablas de control de variabilidad de un proceso se obtendrán mediante el empleo de la desviación estándar muestral.
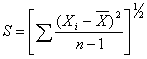
los límites de control 3σ son E(S) ± 3.d.e(S). Para obtener los valores de E(S) y de Var(S) téngase en cuenta lo siguiente:
![]()
Por tanto:
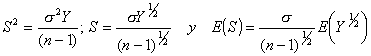
Como Y sigue una chi-cuadrada con n-1 grado de libertad
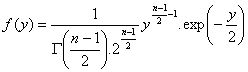
Luego
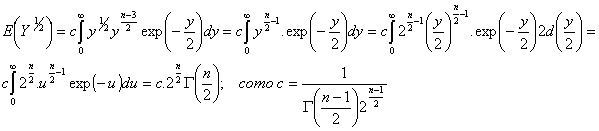
Por tanto

En consecuencia

Para la varianza se obtiene:
Var (S2)=E(S2)-[E(S)]2
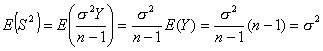
y
![]()
de ahí
![]()
la desviación estándar
![]()
y los límites de control 3σ son
![]()
Como la varianza σ es conocida, estos límites sólo dependen de c4 y c5, que a su vez sólo dependen de n, el tamaño de la muestra. Para los valores usuales de n, se obtiene:
|
n |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
c4 |
0,9213 |
0,9400 |
0,9515 |
0,9594 |
0,9650 |
0,9693 |
0,9727 |
0,9754 |
0,9776 |
0,9794 |
0,9810 |
0,9823 |
|
c5 |
0,3888 |
0,3412 |
0,3075 |
0,2822 |
0,2621 |
0,2458 |
0,2322 |
0,2207 |
0,2107 |
0,2019 |
0,1942 |
0,1872 |
Ejemplo 2
Si σ=2, los límites de control 3σ para la desviación estándar muestral, para una muestra de tamaño n=5, son:
(0,94).2±(3)(0,3412)(2) lo que da el intervalo (- 0,1673 ; 3,9273 ) ;es decir, (0; 3,9273).
El proceso será considerado bajo control siempre que la desviación estándar muestral se halle dentro de los límites de control ya establecidos.
Cuando la media del proceso no se conoce, tampoco se conoce la llamada línea central de la tabla de control. Si la línea central es un valor estimado basado en un gran número de muestras, los límites de control que se obtienen deben de considerarse como límites tentativos. De acuerdo con Shewshart, los límites deben de estar basados, por lo menos, en 20 muestras, cada una con 4 ó 5 observaciones. Shewshart denominó a estas muestras “subgrupos racionales”. Estos deben de determinarse de manera tal que cada subgrupo sea homogéneo y proporcione la máxima oportunidad de variación de un subgrupo a otro.
Sea m el número de muestras y supóngase que ni = n para cada i=1, 2, …, m. Sean
![]()
la media y la desviación estándar en la i-ésima muestra. Se tiene:

Es evidente que
![]()
de manera similar
![]()
Lo cual sugiere que
![]()
Los límites tentativos 3σ para la media muestral cuando no se conocen ni la media ni la desviación típica poblacional son
![]()
y los correspondientes para la desviación estándar son
![]()
La construcción de las tablas de X¯ y S se basa en la distribución normal. La tabla de X¯ es, relativamente, insensible a la hipótesis de normalidad debido al teorema central del límite. Sin embargo, S, es mucho más sensible.
Ejemplo 3
Los datos siguientes son 20 muestras, cada uno con 5 observaciones tomadas en intervalos de 2 horas, de la resistencia a la tensión en libras de un hilo. Constrúyanse las tablas de control X ¯ y S con base en estos datos.
Número
de
muestra
valores de muestra
Media
S
1
44
46 48
52 49
47,8
3,03
2
44
47 49
46 44
46
2,12
3
47
49 47
43 44
46
2,45
4
45
47 51
46 48
47,4
2,30
5
44
41 50
46 50
46,2
3,90
6
49
46 45
46 49
47
1,87
7
47
48 50
46 47
47,6
1,52
8
49
46 51
48 46
48
2,12
9
47
42 48
44 46
45,4
2,41
10
46
48 45
51 50
48
2,55
11
45
47 51
48 46
47,4
2,30
12
52
51 48
48 45
48,8
2,77
13
45
45 47
49 44
46
2,00
14
46
47 43
48 45
45,8
1,92
15
48
49 52
46 51
49,2
2,39
16
44
46 45
47 52
46,8
3,11
17
48
50 47
46 49
48
1,58
18
48
52 51
47 46
48,8
2,59
19
47
51 50
46 49
48,6
2,07
20
44
43 42
43 46
43,6
1,52
![]()
= 47,12
![]()
= 2,327
Al promediar las 20 medias maestrales, para n=5 se obtiene c4=0,94 y c5=0,3412. Luego los límites tentativos de control 3 s para las medias maestrales son
![]()
y los límites tentativos para la desviación estándar muestral son
![]()
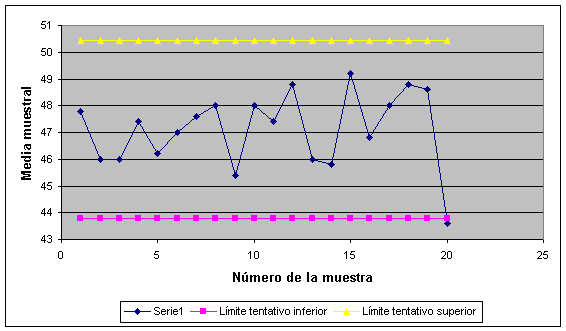
En la figura se observa que la media de la observación 20 se encuentra fuera de control. Si se elimina este último valor, los valores nuevos que se obtienen para los límites tentativos inferior y superior son:
![]()
Es decir:
![]()
Lo que da unos límites (43,92486924; 50,68565708) para la media y de (0, 4,9466) para S.
Tabla para p
Esta tabla se construye cuando se supone que el muestreo se lleva a cabo sobre una distribución binomial de parámetro de proporción p. Para construir los límites de control de las proporciones muestrales, supóngase que no se conoce el valor del parámetro p. Sea m el número de muestras disponibles y Xi el número de unidades defectuosas en la i-ésima muestra de tamaño n: Entonces
![]()
basado en la i-ésima muestra. Y
![]()
es un estimador de p basado en las m muestras. Por tanto los límites 3σ para las proporciones muestrales Xi/n son
![]()
Ejemplo 4
En un proceso de manufactura cada día se seleccionan al azar 100 unidades y se envían para su inspección. Los siguientes datos son el número de unidades defectuosas en la muestra durante 25 días
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
2 |
1 |
4 |
3 |
2 |
2 |
5 |
3 |
4 |
2 |
1 |
5 |
2 |
3 |
2 |
1 |
0 |
6 |
4 |
5 |
2 |
1 |
8 |
3 |
2 |
a) Con base en esta información obténgase una tabla de p.
b) Revísense los límites de control si algún día el proceso se juzgó fuera de control
c) Si se supone que el proceso se encuentra bajo control con un porcentaje de unidades defectuosas, igual al obtenido en la parte b, ¿cuál es la probabilidad de que, en un día determinado el proceso se considere fuera de control?
Solución
![]()
Los límites inferior y superior 3 σ para el porcentaje muestral son:
![]() b) La observación del día 22, cuyo porcentaje es 0,08 está por encima de los
límites de control. Si se elimina esta observación y vuelven a calcularse los
límites de control, los resultados son los siguientes:
b) La observación del día 22, cuyo porcentaje es 0,08 está por encima de los
límites de control. Si se elimina esta observación y vuelven a calcularse los
límites de control, los resultados son los siguientes:
0,02708±0,048697889=(0;
0,0758)
Ahora, todas las observaciones están dentro de los límites de control.
c) Supuesto que el porcentaje de unidades defectuosas es 0,02708; ¿cuál es la probabilidad de que un día, el porcentaje esté por encima de los límites de control?
El porcentaje se distribuye según una N(0,02708; 0,01623263). Por tanto la probabilidad
![]()
Si la decisión que lleva a aceptar o rechazar el lote se toma de acuerdo con las mediciones de los artículos las cuales son magnitudes físicas continuas, entonces se dice que la inspección se lleva a cabo por variables. Si el artículo se clasifica en defectuoso o no defectuoso, y el lote se acepta o rechaza con base al número de artículos defectuosos en la muestra, se dice que la inspección se lleva a cabo por características.
Veamos en primer lugar el muestreo con base en características.
Sea N el tamaño del lote. Entonces un plan básico para la aceptación es seleccionar n artículos del lote de tamaño N y aceptar el lote si el número de artículos defectuosos en la muestra es menor o igual que el número de aceptación c, previamente estipulado. Por ejemplo, un plan de muestreo puede definirse en la forma N=10.000; n=100; y c=1. Es decir, si hay más de un artículo defectuoso el lote será rechazado. El consumidor puede optar entre devolver el lote rechazado al fabricante (inspección no verificable) o someterlo a una inspección del 100% (inspección verificable).
Un criterio muy importante en un plan de muestreo es la probabilidad de aceptar el lote P(A), dada una proporción de artículos defectuosos p. Bajo las hipótesis adecuadas y para algún valor de p y de c, la probabilidad de que el lote sea aceptado con base en una muestra de tamaño n, es la probabilidad binomial acumulativa
![]()
Si np tiene un tamaño moderado, la distribución binomial se puede aproximar por la de Poisson.
![]()
La representación gráfica de P(A) en función de p, se denomina curva de operación (CO). Veamos un ejemplo para n=100 y c=2. Utilizamos la aproximación de Poisson
|
|
Supóngase que ambos están de acuerdo en que un lote es aceptable si la proporción de artículos defectuosos es p≤p1 y no aceptable si la proporción es p≥p2. Se dan las siguientes definiciones que implican riesgos.
Definición 1
El riesgo del productor a es la probabilidad de que el consumidor rechace un lote cuya proporción de artículos defectuosos no es mayor que p1.
Definición 2
El riesgo del consumidor b, es la probabilidad de aceptar un lote cuya proporción de artículos defectuosos es mayor o igual a p2.
El riesgo del productor es la probabilidad de tipo I, del mismo modo que el riesgo del consumidor es la probabilidad de tipo II.
En otras palabras, la situación anterior es análoga a probar la hipótesis nula
![]()
contra la hipótesis alternativa
![]()
p1 recibe el nombre de nivel aceptable de calidad (NAC)
p2 el de tolerancia de la proporción de defectuosos en el lote (TPDL)
La práctica usual ha sido la de escoger la probabilidad de aceptación P(A)=1-a en NAC cercana al punto 0,95 de la curva, y la probabilidad de aceptación P(A)=b en TPDL, cercana al punto 0,10 sobre la curva. Entonces, el 95% de los lotes que provienen de un proceso cuya proporción de artículos defectuosos se encuentra en NAC, o por encima de éste, se aceptará; mientras que sólo el 10% de los que provienen de un proceso cuya proporción de artículos defectuosos se encuentra en TPDL o más, será aceptado.
La esencia del procedimiento está en determinar n y c, dadas las posibilidades de aceptación en el NAC y el TPDL.
Por ejemplo, supóngase un plan de muestreo en el cuál la curva de operación pase a través del riesgo del productor a=0,05 en un NAC de 0,01, y de un riesgo del consumidor b=0,1 en un TPDL igual al 0,05. De esta forma, las probabilidades de aceptación al NAC = 0,01 y al TPDL = 0,05 son 0,95 y 0,1 respectivamente.
Supóngase que las condiciones son tales que la distribución de Poisson proporciona una aproximación adecuada. Sea X la variable aleatoria que representa el número de artículos defectuosos en una muestra de tamaño n.
Entonces para el riesgo del productor, se desea determinar n y c, de manera que:
![]()
de manera similar, el riesgo del consumidor
![]()
Dado
que se conocen a, b, p1 y
p2; hay que determinar n
y c.
No existe ningún método directo de resolución, debido a que n y c tienen que ser enteros. Lo que se hace es determinar 4 planes: 2 contendrán el valor exacto de a y diferirán muy poco de b; y otros dos, contendrán el valor exacto de b y diferirán muy poco de a.
Por ejemplo
Dados los valores a=0,05; b=0,1; p1=0,01; p2=0,05; el procedimiento es el siguiente: sea λ1=np1 y λ2=np2 y fórmese el cociente λ2/ λ1; en el ejemplo, este cociente vale 5.
Tenemos que determinar c, cuando λ2/ λ1=5.
Dado que no es probable obtener de manera exacta este valor, lo que se hace es interpolar con los valores relacionados con el valor 5.
Lo anterior puede lograrse si, iniciando con c=0, se va calculando l1 de manera que la P(A)=0,95 y calculando l2, de manera que p(A)=0,1.
|
|
Número
de |
Valor
de l1=np1 |
Valor
de l2=np2 |
Cociente |
|
0 |
0,05 |
2,30 |
46,00 |
|
|
1 |
0,35 |
3,88 |
11,09 |
|
|
2 |
0,81 |
5,32 |
6,57 |
|
|
3 |
1,36 |
6,68 |
4,91 |
De esta manera se llega a unos valores de c, en este caso c=2 y c=3; donde el cociente entre λ2/ λ1 se aproxime a 5.
Para calcular los valores de n
|
|
Resumiendo, los valores posibles son:
Para el plan c=2 y n=81, la probabilidad de aceptar a un TPDL=0,05 se obtiene mediante l2=(81)(0,05)=4,05. De acuerdo con lo anterior P(A≤2| l2=4,05)= POISSON(2;4,05;VERDADERO)=0,23086824.
Para el plan c=2, n=107, la probabilidad de aceptar para NAC=0,01 se obtiene mediante l1=(107)(0,01)=1,07. Luego P(A≤2 | l1=1,07)= POISSON(2;1,07;VERDADERO)= 0,90638286.
|
Los 4 planes de muestreo para a=0,05; b=0,1; NAC=0,01; TPDL=0,05 |
|||||
|
|
|
|
|
|
|
|
Plan
de muestreo |
Probabilidad
de aceptación |
Probabilidad
de aceptación |
|||
|
n=81,
c=2 |
0,95 |
0,230868242 |
|||
|
n=107,
c=2 |
0,906382857 |
0,1 |
|||
|
n=137,
c=3 |
0,95 |
0,09 |
|||
|
n=134,
c=3 |
0,95 |
0,1 |
|||
La decisión final sobre qué plan adoptar se toma en base a la cercanía a los riesgos especificados.
Cuando esto es posible, se convierte en el tipo de muestreo más popular, puesto que proporciona mucha más información. En general es mas costoso, porque tiene que aplicarse el criterio de aceptación por separado para cada medición de calidad cuando se muestrea por variables.
En el caso sencillo, en el que la aceptación de un lote se hace con base a las medias de la muestra, se supone que la medición de la calidad es una variable aleatoria normalmente distribuida y con varianza conocida.
Sean a el riesgo del productor y ma el promedio del lote para el que la probabilidad de aceptación es 1-a. En forma similar, sea b el riesgo del consumidor y mb el promedio del lote para el cual la probabilidad de aceptación es b. Es decir, si el lote tiene una media ma, se desea aceptar el lote con una probabilidad 1-a, y si éste tiene una media mb (ma>mb) se desea aceptar el lote con una probabilidad b. Dados a, b, ma, mb, el plan de muestreo por variables es una muestra de tamaño n y un valor de aceptación
![]()
de manera que cuando el valor de la media de la muestra
![]()
es mayor que
![]()
el lote será aceptado.
Para obtener estos valores, considérese lo siguiente. Para el riesgo del productor
![]()
o
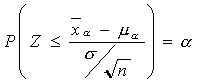
en donde
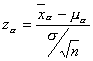
Para el riesgo del consumidor
![]()
o
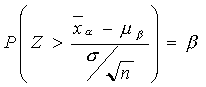
en donde
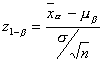
Tenemos dos ecuaciones con dos incógnitas:
![]()
Empleando el método de igualación
![]()
![]()
Al igualar y resolver para n, se obtiene
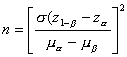
Una vez calculado n, se lleva a cualquiera de las dos expresiones anteriores y se obtiene la 2ª incógnita
Ejemplo
Una compañía constructora de un gran edificio de oficinas se interesa en la resistencia a la comprensión del concreto que se empleará en la construcción del edificio. El proceso a través del cuál se fabrica el concreto con una resistencia promedio de 350 kilogramos por centímetro cuadrado (Kg. /cm2.) es bueno. El concreto adquirido en este proceso debe aceptarse el 95% de las veces. Un proceso que ofrece una resistencia de 347 Kg. /cm2. no es efectivo, y al ser adquirido será rechazado en el 90% de los casos. Si el fabricante de cemento asegura a la compañía que la desviación estándar de su proceso no es mayor de 5 Kg. /cm2. ¿Cuántas muestras de concreto debe inspeccionar el contratista con respecto a su resistencia, y cuál debe ser el valor de aceptación para la media de la muestra bajo las condiciones dadas? Supóngase que la resistencia del concreto se encuentra normalmente distribuida.
Solución
Los riesgos del productor y del consumidor están dados como a=0,05 para ma=350 y b=0,10 para mb=347. Para a=0,05 y 1-b=0,9, los valores cuantiles estandarizados son za=-1,64485348 y z1-b=1,28155194. Aplicando la última formula para n, se obtiene:
![]()
Llevando este valor a la formula anterior, resulta:
![]()
El plan de muestreo consiste en probar la resistencia de 24 muestras de concreto provenientes del proceso y aceptar el concreto siempre que la resistencia promedio sea mayor de 384,32 kilogramos por centímetro cuadrado.
Ejemplo
Una agencia estatal se encarga de vigilar el nivel de concentración de cierto contaminante químico, el cuál ha sido derramado en grandes cantidades en uno de los ríos más grandes del estado. La agencia debe decidir en forma periódica cuándo el nivel de concentración se encuentra entre los límites seguros para permitir la pesca con fines comerciales. La agencia desea obtener un plan de muestreo por variables de tal manera que cuando el nivel de concentración promedio real sea de 5,6 ppm decidirá el 95% de las veces que la pesca continúe. Pero desea prohibir la pesca el 99% de las veces que se observe una concentración hasta de 6,0 ppm. Si la desviación estándar no es mayor de una parte por millón, determínese el plan de muestreo. Supóngase que la distribución de este contaminante se encuentra normalmente distribuida.
Solución
a=0,05 ma=5,6 y b=0,01 y mb=6,0; s=1. El riesgo del productor está en rechazar la validez del nivel de concentración cuando éste es de 5,6. Por tanto:
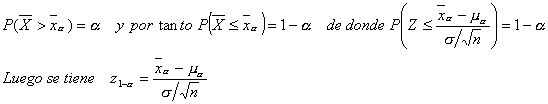
Análogamente el riesgo del consumidor está en aceptar la hipótesis nula cuando ésta es falsa
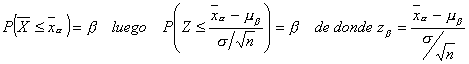
Mirando en la tabla de la normal estándar los valores cuantiles z1-a y zb, se obtiene:
z1-a = 1,64485348 y zb= -2,326347. Llevando estos dos valores a las ecuaciones anteriores se obtienen los valores de
n =99.
![]()
El plan de muestreo consiste en medir el nivel de concentración de 99 muestras y no prohibir la pesca comercial siempre que el nivel medio de la muestra sea inferior a 5,765 ppm.
Ejercicio
Un comprador de grandes cantidades de hilo desea desarrollar un plan de muestreo por variables para la tensión de la ruptura del hilo. El hilo será aceptado por el comprador si la tensión de ruptura es mayor de 60 libras. Se sabe que la desviación estándar del hilo es de 8 libras y dados a=0,05; b=0,05; NAC = 0,95 y TPDL = 0,1. Obténgase el plan de muestreo. Supóngase que la tensión del hilo se encuentra normalmente distribuida.
Solución
Ejercicio.
Supóngase que la calidad de un lote muy grande es de sólo el 5% de unidades defectuosas. Un plan de muestreo para la aceptación requiere una muestra de 40 unidades y un número de aceptación igual a 2 unidades.
a) ¿Cuál es la probabilidad de que el lote sea aceptado?
b) Si la calidad real del lote es de 6,25% de unidades defectuosas, ¿cuál es la probabilidad de que el lote sea aceptado?
Solución
a) n=40 y c=2; p=0,05. Entonces la probabilidad de aceptar el lote es de:
![]()
b) Si p=0,0625. Entonces P(A)= 0,53968901.
Ejercicio.
Para el plan de muestreo n=25 y c=1, empléese la curva CO para obtener TPDL para un riesgo del consumidor del 0,05.
Solución
Empleando la distribución binomial acumulada
|
n=25 |
c=1 |
|
p |
P(A) |
|
0,1 |
0,27121 |
|
0,11 |
0,22206 |
|
0,12 |
0,18047 |
|
0,13 |
0,14567 |
|
0,14 |
0,11680 |
|
0,15 |
0,09307 |
|
0,16 |
0,07371 |
|
0,17 |
0,05804 |
|
0,171 |
0,05665 |
|
0,172 |
0,05529 |
|
0,173 |
0,05396 |
|
0,174 |
0,05266 |
|
0,175 |
0,05139 |
|
0,176 |
0,05015 |
|
0,177 |
0,04893 |
|
0,178 |
0,04774 |
|
0,179 |
0,04658 |
|
0,18 |
0,04544 |
Se obtiene para un valor de p=0,176.
Ejercicio.
Obténgase los 4 planes de muestreo que relacionan los riesgos del productor y del consumidor de a=0,05 para NAC =0,02 y b=0,1 para TPDL=0,08, respectivamente. Solución
Tenemos que calcular n y c.
Sean l1 = np1 y l2 = np2. El cociente de l2/l1=p2/p1= (0,08)/(0,02)=4. Formemos la tabla de la distribución de Poisson:
|
c |
l1 para |
l2 para |
l2/l1 |
|
0 |
0,05 |
2,3 |
46 |
|
1 |
0,35 |
3,88 |
11,0857143 |
|
2 |
0,81 |
5,32 |
6,56790123 |
|
3 |
1,36 |
6,68 |
4,91176471 |
|
4 |
1,97 |
7,99 |
4,05583756 |
|
5 |
2,61 |
9,27 |
3,55172414 |
Los valores de c que se obtienen son c=4 y c=5. Para esos valores se calcula n.
Para c=4, se obtiene: l1=1,97; np1=1,97; n (0,02)=1,97; n=98,5≈99.
l2=7,99; np2=7,99; n(0,08)=7,99; n=99,87≈100.
Para c=5, los valores que se obtienen son: n=131 y n=116.
Problema
Un consejo estatal formado para controlar la calidad del agua selecciona cada semana 5 muestras de agua de una fuente de abastecimiento y determina la concentración promedio de una sustancia tóxica. Los siguientes datos son las cantidades promedio en partes por millón durante 12 semanas.
|
Semana |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Media |
5,2 |
4,9 |
5,5 |
5,4 |
4,8 |
4,6 |
5,5 |
4,7 |
5,1 |
4,5 |
5,8 |
5,6 |
a) Si los valores de la concentración promedio y de la desviación estándar son 5 y 0,5 ppm, respectivamente, obténgase los límites de control 3s para la concentración promedio. Para este periodo, ¿existió alguna razón para alarmarse?
b) Si se considera como peligrosa una concentración de 6 ppm, ¿qué tan probable es tener un resultado como el anterior, con base en 5 muestras de agua, si la concentración real promedio es de 5 ppm?
c) Mediante el uso de los límites de control de la parte a, ¿cuál es la probabilidad de detectar un desplazamiento en el valor de la concentración media de 5 ppm a 5,25 ppm?
Solución
a) 4,32917961 y 5,67082039.
b) 1-DISTR.NORM(6;5;0,5/5^0,5;VERDADERO)= 3,87556E-06
c) Para calcular dicha probabilidad
![]()
Ejercicio
Los siguientes datos son las tensiones promedio de ruptura de 6 muestras de metal tomadas de forma periódica
|
Muestra |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Media |
498,6 |
508,3 |
484,6 |
505,7 |
491,7 |
495,4 |
482,6 |
515,2 |
510,8 |
503,7 |
Se sabe que los valores de tensión de ruptura promedio y de desviación estándar son 500 y 20 libras, respectivamente.
a) Obténgase los límites de control 3s para la tensión de ruptura media de la muestra y hágase una gráfica de la tabla de control. ¿Existe alguna media muestral que se encuentre fuera de los límites de control?
b) Obténgase la probabilidad de no detectar un corrimiento en el valor real de la tensión de ruptura promedio de 500 a 494 libras.
c) Obténgase los límites de control 3s para la desviación estándar muestral.
Solución
a) Los límites de control 3 s son: 475,505103 y 524,494897.
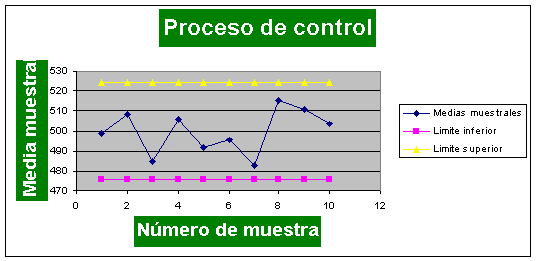
No existe ninguna media fuera de los límites de control.
b) La probabilidad de no detectar un corrimiento de la media de 500 a 494 es igual a
![]()
c) Los límites de control son c4s ±3sc5 donde tanto c4 como c5 sólo dependen de n. Los valores de c4 y c5 para n=6 son:
c4=0,9515 y c5=0,3075
Luego el intervalo de control para la desviación típica es de 0,57783183 a 37,4834826.
Ejercicio
Las tablas de control de X¯ y S de un proceso de llenado de recipientes se conservan por algún tiempo. Con base en 25 muestras periódicas, cada una con 5 recipientes se obtiene que
![]()
a) Si se supone que el proceso de llenado se encuentra bajo control ¿Cuáles son los límites de control de la media y de la desviación estándar muestral?
b) Obténgase un estimado de la desviación estándar del proceso.
Solución
Sabemos que
![]()
de manera similar
![]()
Lo cual sugiere que
![]()
Los límites tentativos 3σ para la media muestral cuando no se conocen ni la media ni la desviación típica poblacional son
![]()
y los correspondientes para la desviación estándar son
![]()
Luego, llevando los datos a las formulas se obtiene:
Para la media
![]()
Siendo c4=0,94. Lo que da: 378,362655 y 422,037345 para la media y 0 a 31,9594754 para la desviación típica.
b) Un estimador de s podría ser
![]()
lo que da (15,3)/(0,94)=16,2765957.
Ejercicio
En un proceso de manufactura, cada día se seleccionan al azar 100 unidades y se envían para su inspección. Los siguientes datos son el número de unidades defectuosas en la muestra durante 25 días.
|
Día |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Unidades |
2 |
1 |
4 |
3 |
2 |
2 |
5 |
3 |
4 |
2 |
1 |
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Día |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
|
Unidades |
3 |
2 |
1 |
0 |
6 |
4 |
5 |
2 |
1 |
8 |
3 |
2 |
|
a) Con base en esta información, obténgase una tabla de p.
b) Revísense los límites de control si algún día el proceso se juzgó fuera de control.
c) Si se supone que el proceso se encuentra bajo control con un porcentaje de unidades defectuosas, igual al obtenido en la parte b, ¿cuál es la probabilidad de que, en un día determinado el proceso se considere como fuera de control?
Solución
a) De la muestra se obtiene:
|
Media |
2,92 |
y los límites tentativos para las proporciones maestrales X/n son:
![]()
lo que da unos límites de 0 y 0,07971002.
b) La observación del día 23 queda fuera de los límites de control. Eliminando esta última información, el nuevo valor estimado de p es 0,02708333 y el resultado es: 0 y 0,07578122.
c) Supuesto que el porcentaje es 0,0271, la probabilidad de que un día determinado el proceso se juzgue fuera de control es:
![]()