|
Para volver al menú principal pulse sobre la palabra |
|---|
1. Introducción
2. Muestras ordenadas.
3. Particiones ordenadas de un n-conjunto A en k subconjuntos
4. Distribuciones y llenados
5. Secuencias
Para el desarrollo del tema se utilizan unas reglas básicas de la teoría de conjuntos:
Regla de la suma. Dado un conjunto finito A cualquiera, y una familia de subconjuntos; A1, A2, A3, ..., AnÎ P(A) tales que
se verifica:
.
Regla del producto.
Sean
A1, A2,
A3, ..., An
una familia de conjuntos finitos cualesquiera, entonces se verifica:
En matemáticas el concepto de muestra se utiliza tanto para designar el procedimiento mediante el cual se extrae un subconjunto de un conjunto dado como al mismo subconjunto extraído. Normalmente vamos a utilizar esta última acepción y nos fijaremos sólo en el resultado de la operación, en el subconjunto elegido.
Sea (a1, a2, ..., ar) una r-muestra de un n-conjunto A donde cada ai ÎA; i=1, 2, …, r. Al número r se le llama volumen de la muestra. Si en la elección de la muestra se tiene en consideración el orden en la sucesión de los elementos, hablaremos de r-permutaciones; si el orden en el que se encuentran en la sucesión no se tiene en consideración, hablaremos de las r-combinaciones. El que el orden se tome o no en consideración viene implícito en la misma naturaleza del problema y a veces un mismo problema puede resolverse haciendo ambas consideraciones.
A su vez, los elementos en la muestra pueden aparecer repetidos o no. Entonces hablaremos de r-permutaciones con repetición y de r-combinaciones con repetición. Una r-permutación con repetición se llama una palabra de longitud r del alfabeto A de n letras.
Históricamente el primer problema que se planteó fue el contar el número de r-muestras de un n-conjunto
Designemos por P(n;r) el número de r-permutaciones de un n-conjunto. Para calcular este número podemos hacer el siguiente razonamiento. El primer elemento de la r-muestra podemos elegirlo de n maneras distintas; elegido el primero, para elegir el segundo, en el supuesto de que no pueden aparecer elementos repetidos, disponemos de n-1 elementos; y así hasta el r-ésimo, que disponemos de n-r+1 elementos. Para el cálculo del número total podemos aplicar la regla del producto y tendremos que:
P(n;r) = n.(n-1). … (n-r+1).
Haciendo n=r se obtiene:
P(n;n) = n!
Que se corresponden con lo que normalmente se conoce como las permutaciones de n elementos.
Y para completar el resultado, imponemos que:
P(n;0) = 1.
Si lo que queremos es calcular el número de r-permutaciones con repetición, el razonamiento se simplifica pues para elegir el primer elemento disponemos de n elementos, igualmente para el segundo, en el supuesto en que se puedan repetir, disponemos tambien de n elementos. Así hasta el r-ésimo, para el cual disponemos también de n elementos. En total habrá:
configuraciones diferentes.
El cálculo del número de r-permutaciones se presenta en la práctica de muy diversas formas, por ejemplo en la teoría de la probabilidad asociado con la regla de Laplace, para calcular el número de las configuraciones favorables a la realización de un suceso y el número de las configuraciones posibles. Esto se simplifica mediante el esquema de urnas. De un urna que contiene n bolas distintas, se extraen sucesivamente r bolas:
Sin reemplazamiento, sin devolución a la urna de la bola extraida.
Con reemplazamiento, la bola se extrae e inmediatamente se devuelve a la urna.
En el primer caso el número de posibilidades son las r-permutaciones sin repetición del n-conjunto formado por las n bolas. Y en el segundo, son las r-permutaciones con repetición del mismo n-conjunto.
Aduzcamos un ejemplo más. Si A es un n-conjunto, al que vamos a suponer ordenados sus elementos
sabemos que el conjunto de partes de A, P(A) tiene exactamente 2n elementos. Es decir que ½P(A)½=2n . Para demostrarlo, consideremos un subconjunto cualquiera (ai1, ai2, ... air ) de r elementos, donde r=0, 1, 2, …, n. Para r=0 suponemos que tenemos el conjunto vacío, esta r-muestra la podemos poner en correspondencia con una n-muestra formada por elementos de dos tipos; ceros y unos, los unos en las posiciones i1, i2, ..., ir ; los ceros en los lugares restantes. De manera que a todo subconjunto, incluido el vacío al que le correspondería (0,0, …, 0), le correspondería una n-muestra formada por ceros y unos; y, recíprocamente a cada n-muestra de este tipo se le asociaría un subconjunto, sustituyendo los lugares en los que aparecen los unos por los elementos correspondientes. Obviamente esta correspondencia es biunívoca, a cada subconjunto se le hace corresponder una única n-muestra y recíprocamente a cada n-muestra se le hace corresponder un único subconjunto. Por tanto el número de subconjuntos será igual al número de n-permutaciones con repetición del 2-conjunto {0, 1} que como sabemos es igual a 2n .
Este ejemplo se puede también interpretar como el cálculo del número de vértices de un hipercubo en un espacio de n dimensiones. En efecto, sean x1, x2, ..., xn los ejes de las n dimensiones del espacio, cada vértice se puede considerar como una n-permutación con repetición del 2-conjunto {0, 1} , el origen de coordenadas, se correspondería con el (0,0,…,0); los vértices de cada uno de los ejes con un 1, en la coordenada correspondiente y cero en las otras. Las intersecciones de los sucesivos hiperplanos, por los unos en las correspondientes coordenadas, etc.
Otro ejemplo, ¿cuántas matrices diferentes de dimensión mxn se pueden construir con ceros y unos?. Evidentemente habría 2mxn .
Para hallar el número de las r-combinaciones de un n-conjunto, es decir de las r-muestras de un n-conjunto en las que no se tienen en cuenta el orden de la sucesión de los elementos o lo que es lo mismo los subconjuntos de r elementos del n-conjunto A; razonemos de modo siguiente:
Por cada
una de las r-combinaciones, tendremos r! r-permutaciones distintas, si tomamos
en consideración el orden en el que aparecen. Por tanto, si designamos con
el número de tales r-combinaciones
o con
, tendremos que:
=
=
=
.
Fórmula que nos da las r-combinaciones de un n-conjunto. Si en la fórmula sustituimos r por n-r el resultado es el mismo, obteniéndose la siguiente importante igualdad:
que puede interpretarse también como que el número de subconjuntos de dimensión r es el mismo que el de conjuntos de dimensión n-r. Lo que es obvio, pues por cada subconjunto de r elementos hay uno y sólo un conjunto de dimensión n-r, que es su complementario.
Las fórmulas se completan, añadiendo los siguientes resultados:
=1
Otra formula importante para los números combinatorios es la siguiente:
que puede deducirse algebraicamente, pero que se interpreta de una manera fácil y cómoda de la siguiente forma: El número de subconjuntos de r elementos de un conjunto de n elementos, se puede calcular si nos fijamos en un elemento determinado y calculamos, cuántos subconjuntos no contienen a ese elemento, es decir cuántos subconjuntos de r elementos se pueden construir con los restantes n-1 elementos; y cuántos hay que contienen a ese elemento, es decir cuántos subconjuntos de r-1 elementos se pueden construir con los otros n-1 elementos, donde ya hemos quitado el elemento que vamos a añadir al final.
Esta última fórmula se puede entender como una forma recursiva de calcular las combinaciones y es en suma el sustento matemático del famoso triángulo de Tartaglia.
Un resultado importante que se obtiene de la interpretación de las r-combinaciones como el número de subconjuntos de n elementos de un n-conjunto es el siguiente:
Para calcular su número procedamos de la manera siguiente:
Los r1
elementos del primer subconjunto podemos elegirlos de
formas. Elegidos estos, los
siguientes
elementos del segundo conjunto, puesto que son disjuntos,
habrá que elegirlos de entre los n -
elementos restantes, lo que puede hacerse de
formas. Análogamente para los
restantes subconjuntos, hasta llegar al último en que los
elementos habrá que elegirlos de entre los
n
-
elementos restantes. Lo que puede hacerse de
formas. En total y aplicando la
regla del producto tenemos:
…
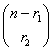formas distintas de elegir.
Desarrollando queda que:
…
=
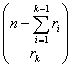El último 0! En realidad es
puesto que
.
Simplificando y teniendo en cuenta que todos los numeradores, salvo el primero, se simplifican con los denominadores anteriores, queda:
…
=
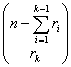.Fórmula que equivale en el desarrollo clásico a las permutaciones con
repetición de n elementos en donde hay
de ellos iguales o indistinguibles entre sí;
de ellos distintos de los anteriores pero igualmente indistinguibles entre sí;
y así, hasta los últimos
elementos, distintos de todos los anteriores pero iguales entre sí.
Por último
y para terminar esta primera parte, calculemos mediante un razonamiento el número
de r-combinaciones con repetición del n-conjunto A, al que vamos a suponer que
tiene sus elementos ordenados, es decir A=
.
Agreguemos a cada r-combinación los n elementos a1a2...an tratados como simbólicos de A, agrupemos los elementos iguales y ordenémoslos por sus índices, a continuación separemos los elementos distintos mediante n-1 barras y sustituyamos todos los elementos por puntos. Tendremos un total de n+r puntos que hemos de separar mediante n-1 barras a colocar en n+r-1 posiciones entre n+r puntos. Esto como sabemos puede hacerse de :
formas
Ejemplifiquemos mediante un ejemplo esta situación:
Consideremos las 4-combinaciones con repetición de los elementos de A={a, b, c, d, e} , sea (aace) una de ellas. Agreguemos a esta los 5 elementos de A: (aaceabcde) y a continuación ordenémosles, resultando (aaabccdee), coloquemos 4 barras que separen los elementos distintos (aaa/b/cc/d/ee ) y sustituyamos los elementos por puntos (. . . / . / . . / . / . . ). El problema consiste en calcular las diferentes formas de colocar 4 barras en 8 lugares que dejan entre sí 9 puntos. Esto como sabemos es igual a:
.
Un conjunto de objetos (tuercas, granos, coches, etc.) se distribuye en un conjunto de celdas (cajas, silos, fábricas, etc.) y como consecuencia se llenan. Ambos conceptos, distribución (su sinónimo es partición) y llenado, se emplean para designar tanto el conjunto de operaciones mediante las cuales se obtiene la configuración buscada como para señalar el resultado de tales operaciones, es decir, la situación obtenida.
El interés hacia esta clase de problemas no se extingue pues gozan de gran importancia práctica y además se cuenta con un procedimiento de resolución bastante elaborado. Ello se muestra en los más diversos planteamientos: particiones de conjuntos, cortes de grafos y de redes, agrupaciones de tornos y mecanismos automáticos y robótica, etc.
Para abordar la gran variedad de situaciones que se pueden presentar conviene hacer una serie de consideraciones sobre las condiciones impuestas a los tipos de elementos a distribuir, sobre los métodos de distribución empleados; y, también, sobre la capacidad de las células a llenar. En un primer momento, haremos las siguientes distinciones: que los elementos a distribuir sean distinguibles o no lo sean, y que las células, a su vez sean también distinguibles o no. En total se presentan 4 posibilidades:
A.
Que los elementos a distribuir sean
distinguibles y las células también lo sean.
B.
Que los elementos a distribuir sean
indistinguibles y las células distinguibles.
C.
Que los elementos a distribuir sean
distinguibles y las células no.
D.
Que ni los elementos sean distinguibles ni
las células.
De aquí en adelante designaremos con N al n-conjunto de elementos a distribuir y con R al r-conjunto de células.
A. En este caso los elementos de N como los de R son distinguibles, bien sean por el color, el peso o el número o por cualquier otra característica; lo único que nos interesa es que se pueden diferenciar. Consideremos el caso en el que en cualquiera de las r células puede ir cualquiera de los n elementos y la célula se llena con uno de estos n elementos, no puede haber células vacías. El número total de distribuciones es de :
Este caso se puede presentar de diversas formas equivalentes:
1. Formación de palabras de longitud r de un alfabeto de n letras.
2. Extracción con devolución de r bolas de una urna que contiene n.
3. Formación de las r-permutaciones con repetición de n símbolos.
La restricción de que cada elemento debe de estar a lo sumo en una célula (dos células distintas no pueden contener al mismo elemento), se corresponde la imposición del carácter de que las aplicaciones entre las células y los elementos sea biunívoca. Para la primera célula podemos escoger cualquiera de los n elementos, para la segunda nos quedarían n-1, para la r-ésima nos quedarían n-r+1. En este caso el número de configuraciones distintas es de:
A la clase (A) pertenecen las siguientes casos de distinción entre elementos y células.
(A1)
los elementos del n-conjunto N poseen una (
-especificación si cuenta con k1 elementos del primer tipo ( por
ejemplo color), k2 elementos del segundo tipo, …, km
elementios del m-ésimo tipo y además
.
(A2)
El r-conjunto R posee una
-especificación si en cada célula se disponen de
i=1, 2, …,
r.
(A3) Los elementos dentro de la células están ordenados, es decir, dos células se consideran llenas de manera diferente, si es distinta la ordenación de los elementos (incluso de los mismos) alojados en ellas; no hay limitación para el volumen de las células.
Aduzcamos un ejemplo de cada una de estas modalidades; empecemos por el primero:
Supongamos que el n-conjunto posee una (p,q)-especificacación, es decir, hay p bolas de un color y q de otro y p + q = n, y no hay limitación para el número de bolas en una celda. En este caso tenemos que p bolas del mismo color se distribuyen en r celdas distintas de :
formas. El razonamiento sería: agregar r bolas simbólicas, una por cada celda, y agrupar ordenadas por celdas las bolas que van a las mismas celdas. El problema equivalente sería trazar r-1 líneas en p + r –1 posiciones que hay entre p + q bolas.
Análogamente, las q bolas se repartirían en:
formas. Aplicando la regla del producto quedaría:
Y, en general, si tenemos una ( k1, k2, ..., km) -especificación del n-conjunto N, el número de configuraciones distintas es igual a:
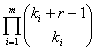
Pasemos ahora a analizar los problemas de la clase (A2). Empecemos por una especificación sencilla, dos celdas en la primera de las cuales hay n1 elementos y en la segunda n2, en total n1 + n2 = n.
Este problema es equivalente a escoger n1 elementos de entre n para la primera urna, y escogidos estos n1 elementos, de entre los n – n1 restantes, escoger los n2. En total, aplicando la regla del producto, tenemos:
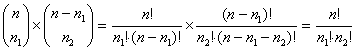
Generalizando,
para el caso en que tengamos una
-especificación del r-conjunto R, siendo
, el número de configuraciones distintas vendrá dado por:
.
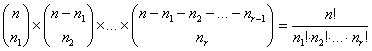Que
equivale a la partición ordenada del n-conjunto N en r subconjuntos disjuntos,
donde le primer conjunto tiene
elementos, el segundo
, …, el r-ésimo
.
A cada una de las n! formas de ordenar los n elementos, les agregamos r elementos simbólicos, uno por cada celda, de manera que tendremos n+r elementos, que dejan entre sí n+r-1 espacios, para trazar r-1 líneas entre ellos, lo que podremos hacer de:
.
O también se puede pensar de la manera siguiente:
Para cada una de las n! formas de ordenar los n elementos, si suponemos que no hay células vacías, hay
formas. Si suponemos que pueden haber r = 0, 1, 2, …, r-1 celdas vacías, el número de configuraciones será igual a:
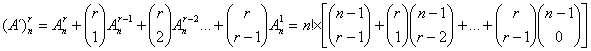
(B). Que los elementos a distribuir sean indistinguibles y las células distinguibles.
Distingamos varios casos.
Que los elementos del conjunto N se distribuyan en r celdas de manera que ninguna quede vacía.Este caso equivale a trazar r-1 líneas entre n-1 posición que dejan n elementos.
A este caso se le asocia el tipo de problemas siguiente:
a. Pintar usando r colores diferentes (se utilizan todos los colores al menos una vez) n bolas idénticas.
b. ¿Cuántas combinaciones con repetición de orden r hay que utilicen los n elementos?
Obviamente,
.En este caso habría:
2. Que los elementos del conjunto N se distribuyan en las r celdas de manera que puedan quedar celdas vacías. Este caso se resuelve agregando r elementos simbólicos, que suponemos numerados, uno por cada celda. Los N elementos van junto con los r elementos simbólicos, agrupados y ordenados según vayan a una celda u otra. Si un celda va vacía entonces el elemento simbólico que tiene ese número de celda va sólo. En total el número de configuraciones buscadas es igual al número de procedimientos de trazar r-1 líneas entre n+r-1 posición que dejan entre sí n +r elementos. Es decir:
a. A este caso pertenece el de la búsqueda de las soluciones enteras no negativas de la ecuación:
Donde se permite que algunas incógnitas tomen valores nulos.
b. El número de monomios distintos de un polinomio homogéneo de grado 9 por ejemplo en tres indeterminadas, también por ejemplo.
c. El número de derivadas parciales de un determinado orden ( por ejemplo n) de una función en tres variables ( o r variables) en la que son válidos todos los teoremas de Schwarz.
3.
En fin, a este caso pertenecen los problemas relacionados con el cálculo
del número de muestras de un n- conjunto. Por ejemplo ¿cuántas muestras,
extraídas con reemplazamiento, de tamaño r, pueden seleccionarse de una
población de tamaño n, considerando dos muestras distintas si; o bien, tienen
un elemento distinto; o bien, si teniendo los mismos, se repiten diferentes números
de veces? Obviamente, el número de tales muestras es de:
Los problemas de la clase ( C ) y (D) en los que las celdas para su llenado son indistinguibles son considerablemente más complejos y se conocen genéricamente con el nombre de particiones no ordenadas.
Los problemas de la clase ( C ) en donde los elementos del N conjunto son distinguibles permiten su resolución. Distingamos varios casos.
1.
Los elementos del N conjunto se distribuyen en las r células de manera
que no hay células vacías y además se tiene en consideración el orden en el
que los elementos caen en las células.
En tal caso
para cada una de las n! formas de
ordenar los n elementos tenemos
formas de trazar r-1 líneas en n-1
posición entre n elementos. Si a este número lo dividimos por las r! formas
que tenemos de ordenar las celdas, puesto que son indistinguibles, nos queda:
2. Si se modifica el apartado 1. De manera que se admite que pueda haber células vacías. Es decir, supongamos que hay 0, 1, 2, …, r-1 células vacías. En tal caso resulta:
.
3. Si no hay células vacías, mientras que el orden de disposición de los elementos en las células no se toma en consideración. En tal caso el número de distribuciones será igual a:
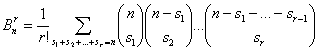
donde la
suma
se extiende a todas las soluciones enteras no negativas tales que
, con i = 1, 2, …, r. Desarrollando esta fórmula se obtiene:
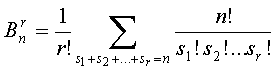
Fórmula que se conoce como de Stirling de 2º orden y se designa con el símbolo S (n; r).
1. Si se admite la posibilidad de que puedan haber células vacías y sigue manteniéndose la consideración de no tener en cuenta el orden en que los elementos caen en las células. La fórmula que se obtiene que resulta de suponer que hay 0, 1, 2, …, r-1 células vacías, es la siguiente:
.
Por último, pasemos al caso (D) en el que tanto las células como los elementos a distribuir, se consideran indistinguibles. En este caso la teoría de su resolución aún no está completamente elaborada. La interpretación más conocida del caso la representa el problema teórico numérico sobre la partición de los números naturales en sumandos naturales. Los problemas de esta clase no pueden ser equiparados a los de las clases anteriores, las conexiones resultan ser mucho más complejas y no se acierta a haalar una expresión analítica conveniente para obtener el número buscado. Por lo pronto, para calcular el número de tales particiones, sirve de base fundamental el siguiente método recurrente.
Supongamos
que el n-conjunto S se divide en k partes no vacías
con la particularidad de
para i = 1, 2, …, k.
Denotando
con
el número de tales particiones. Se tiene:
En
cualquier sucesión ordenada de elementos de dos clases se llama secuencia a toda subsucesión máxima de elementos de la misma
clase. Por ejemplo, la sucesión
se inicia con una secuencia de
de longitud 4, y es seguida por secuencias de longitud 3, 1, 1, 3, 3
respectivamente. A cada secuencia de alfas sigue una de betas y a cada una de
beta sigue una de alfas; el número total de secuencias es siempre, como mínimo,
2 y como máximo, el doble más uno del número de vecinos distintos en la
sucesión dada. El doble del menor de ellos más uno.
Pruebas de aleatoriedad. El problema consiste en decidir si una observación dada es atribuible al azar o si hay que examinarla para asignarle causas. Por ejemplo, supongamos el arreglo siguiente:
v o v v v o v v v v v o v v o v v v v o v
correspondiente a los asientos vacíos y ocupados de la barra de un restaurante. Nótese que no hay dos asientos ocupados que sean adyacentes. ¿Puede esto deberse al azar?. Si son 5 asientos ocupados y 16 vacíos, es imposible obtener más de 11 secuencias, y este fue el número realmente observado. Más adelante se demostrará que si todos los arreglos fuesen igualmente probables, la probabilidad de 11 secuencias sería de 0,00578… Esta probabilidad pequeña confirma en cierta medida el presentimiento de que las separaciones observadas son intencionales. Esta suposición no se puede demostrar por métodos estadísticos, pero se obtienen más pruebas de ello si se hacen observaciones repetidas. Si la barra fuese frecuentada por familias habría una tendencia de los ocupantes a agruparse, la cual conduciría a un número de secuencias relativamente pequeño. De la misma manera , al contar secuencias de niños y niñas en un salón de clases, podríamos descubrir una mezcla que esté en mejor o en peor grado de aleatoriedad.