
 |
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema
1. Introducción
2. Prueba de bondad de ajuste chi-cuadrado
3. El estadístico de Kolmogorov-Smirnov
4. Prueba de chi-cuadrado para el análisis de tablas de contingencia con dos criterios de clasificación
En este capítulo se examinarán pruebas de hipótesis en las que la característica que se desconoce es alguna propiedad de la forma funcional de la distribución que se muestrea. Además se discutirán pruebas de independencia de dos variables aleatorias en las cuales la evidencia muestral se obtiene mediante la clasificación de cada variable aleatoria en un cierto número de categorías. Este tipo de prueba recibe el nombre de bondad de ajuste. Para un tamaño específico del error de tipo I, la hipótesis nula será rechazada si existe una diferencia suficiente entre las frecuencias observadas y las esperadas.
La hipótesis alternativa es compuesta y a veces no suele estar identificada. El resultado es que la función potencia es difícil de obtener. En consecuencia, una prueba de bondad de ajuste no debe usarse por sí misma para aceptar la afirmación de la hipótesis nula.
Se utiliza para decidir cuando un conjunto de datos se ajusta a una distribución dada
Considérese una muestra aleatoria de tamaño n de la distribución de una variable aleatoria X dividida en k clases exhaustivas e incompatibles, y sea Ni i = 1, 2, …, k. el número de observaciones en la i-ésima clase. Considérese la hipótesis nula
H0: F(x)=F0(x)
en donde el modelo de probabilidad propuesto F0(x) se encuentra especificado de manera completa, con respecto a todos los parámetros.
Es posible, pues, calcular pi: probabilidad de obtener una observación en la i-ésima clase, bajo H0. Es obvio, también, que
![]()
Sea ni la realización de Ni para i = 1,2,…, k de manera que
![]()
La probabilidad de obtener de manera exacta ni observaciones en la i-ésima clase es
![]()
Dado que existen k categorías mutuamente excluyentes con probabilidades p1, p2, …, pk; entonces bajo la hipótesis nula la probabilidad de la muestra agrupada es igual a la función de probabilidad de una distribución multinomial determinada.
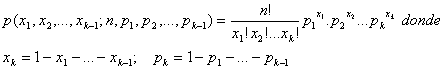
Para deducir una prueba estadística para H0, considérese el caso de k = 2. Este es el caso de la distribución binomial con x = n1, p = p1, n-x =n2 y 1-p =p2. Sea la variable aleatoria estandarizada:
![]()
para n grande, esta variable aleatoria se distribuye según una N(0;1). Además sabemos que el cuadrado de una variable aleatoria N(0,1) se distribuye según una chi-cuadrado con un grado de libertad. Entonces el estadístico

Si se sigue este razonamiento, puede demostrarse que para k≥2 categorías distintas
![]()
Nótese que Ni es la frecuencia observada en la i-ésima clase y npi la esperada bajo la hipótesis nula.
Esta estadística recibe el nombre de prueba de bondad de ajuste chi-cuadrada de Pearson.
Si existe una concordancia perfecta entre las frecuencias observadas y las esperadas, el estadístico tendrá un valor igual a cero; por otra parte si las discrepancias entre estas frecuencias son grandes, el estadístico tomará un valor, también muy grande. Por ello se desprende que para un valor dado del error de tipo I, la región crítica estará en el extremo superior la distribución chi-cuadrada con k-1 grado de libertad.
Una ventaja de la prueba de bondad de ajuste chi-cuadrada es que para valores grandes de n, la distribución límite chi-cuadrada de la estadística, es independiente de la forma que tenga la distribución F0(x) propuesta en la hipótesis H0. Como consecuencia de esto se tiene que la prueba de bondad se utiliza también para distribuciones de probabilidad en las que F0(x) es continua. Sin embargo, debe insistirse en que la prueba de bondad es discreta, en el sentido de que ésta compara frecuencias que se observan y se esperan para un número finito de categorías.
De acuerdo con lo anterior, si F0(x) es continua, la prueba no compara las frecuencias que se observan aisladas con la función de densidad propuesta tal y como implica la hipótesis nula; sino, más bien, la comparación se lleva a cabo aproximando la distribución continua bajo H0 con un número finito de intervalos de clase.
No obstante, esta prueba es un procedimiento razonablemente adecuado para probar suposiciones de normalidad siempre y cuando el tamaño de la muestra sea suficientemente grande.
¿Qué tan grande debe ser el tamaño de la muestra? Se ha encontrado que con n igual a 5 veces el número de clases, los resultados son aceptables. Una regla conservadora es que ninguna clase tenga una frecuencia inferior a 5; si esto sucediera, se agruparían clases vecinas.
A menos que se especifique una
hipótesis alternativa que consista en un modelo alternativo particular F1(x),
la potencia de la prueba (probabilidad de que un valor se encuentre en la región
crítica cuando H0 es falsa) es muy difícil de determinar. Por otra
parte, puede demostrarse que la potencia tiende a 1 cuando n
tiende a infinito. Esto implica que cuando n es muy grande es casi seguro que se rechaza H0, pues es
muy difícil especificar una F0(x) lo suficientemente cercana a la
distribución. Por tanto esta prueba es cuestionable para muestras muy grandes.
Recuérdese que el modelo de probabilidad propuesto F0(x) se especificó completamente. Por regla general, solo se conoce la normalidad de F0(x), necesitándose estimar la media y la varianza, en consecuencia las frecuencias esperadas npi; i =1,2,…,k no pueden determinarse.
Sea T el estadístico del parámetro desconocido θ de F0(x). Tanto Ni (frecuencias observadas) como npi(T) frecuencias esperadas son variables aleatorias, donde pi(T) indica que la probabilidad bajo la hipótesis nula es función del estadístico T de θ.
Puede demostrarse que si T es el estimador de máxima verosimilitud de θ, entonces:
![]()
en donde r es el número de parámetros que se está intentando estimar.
El gerente de una planta industrial pretende determinar si el número de empleados que asisten al consultorio médico de la planta se encuentran distribuido en forma equitativa durante los 5 días de trabajo de la semana. Con base en una muestra aleatoria de 4 semanas completas de trabajo, se observó el siguiente número de consultas:
|
Lunes |
Martes |
Miércoles |
Jueves |
Viernes |
|
49 |
35 |
32 |
39 |
45 |
Con a=0,05, ¿existe alguna razón para creer que el número de empleados que asisten al consultorio médico, no se encuentra distribuido de forma equitativa durante los días de la semana?
Solución
Una distribución uniforme lleva consigo que la probabilidad sería la misma para cada día de la semana. Por tanto pi=0,2 para i = 1, 2, 3, 4, 5.
La hipótesis nula H0: pi=0,2 para i = 1, 2, 3, 4, 5. Dado que n=200, la frecuencia esperada para cada día de la semana es 200*0,2=40. Luego, el valor del estadístico es:
|
Días |
Frecuencias |
Frecuencias |
(Ni-npi)2/npi |
|
Lunes |
49 |
40 |
2,025 |
|
Martes |
35 |
40 |
0,625 |
|
Miércoles |
32 |
40 |
1,6 |
|
Jueves |
39 |
40 |
0,025 |
|
Viernes |
45 |
40 |
0,625 |
|
|
|
Suma |
4,9 |
El estadístico sigue una chi-cuadrada con k-1 grado de libertad, con k=5. Luego
![]()
Por otro lado PRUEBA.CHI.INV(0,05;4)= 9,48772846. Como 4,9<9,48772846, no puede rechazarse la hipótesis nula.
En la tabla siguiente se dan las calificaciones obtenidas en la prueba de matemáticas SAT por los estudiantes de tercer año preparatorio
|
De
…...…..a...……. |
Número de |
Frecuencia |
Intervalo
normal |
Probabilidad |
Número |
||
|
200 |
249 |
3423 |
0,00716 |
-2,425 |
-2,017 |
0,0142 |
6795,55 |
|
250 |
299 |
18434 |
0,03855 |
-2,008 |
-1,600 |
0,0325 |
15539,08 |
|
300 |
349 |
39913 |
0,08347 |
-1,592 |
-1,183 |
0,0626 |
29939,08 |
|
350 |
399 |
51603 |
0,10791 |
-1,175 |
-0,767 |
0,1016 |
48604,67 |
|
400 |
449 |
61691 |
0,12901 |
-0,758 |
-0,350 |
0,1390 |
66489,75 |
|
450 |
499 |
72186 |
0,15096 |
-0,342 |
0,067 |
0,1603 |
76642,67 |
|
500 |
549 |
72804 |
0,15225 |
0,075 |
0,483 |
0,1557 |
74444,01 |
|
550 |
599 |
58304 |
0,12193 |
0,492 |
0,900 |
0,1274 |
60930,11 |
|
600 |
649 |
46910 |
0,09810 |
0,908 |
1,317 |
0,0879 |
42021,58 |
|
650 |
699 |
30265 |
0,06329 |
1,325 |
1,733 |
0,0511 |
24420,10 |
|
700 |
749 |
16246 |
0,03397 |
1,742 |
2,150 |
0,0250 |
11957,60 |
|
750 |
800 |
6414 |
0,01341 |
2,158 |
2,575 |
0,0104 |
4991,80 |
|
|
|
478193 |
1,00000 |
|
|
0,9678 |
462776,00 |
los datos están ajustados a una normal de media 491 y desviación típica 120. Con base en la prueba de bondad de ajuste chi-cuadrado, ¿existe alguna razón para creer que el número de respuestas correctas no se encuentra distribuidas según una N(491; 120) a un nivel a=0,05?
Solución
Nótese que la sumas de las probabilidades no es la unidad y por tanto la clasificación en clases no es exhaustiva; sin embargo, mediante un reajuste esto puede lograrse, haciendo que la primera clase no tenga límite inferior ni la última superior. La P(X ≤250)= 0,02230387 y la P(X≥750)= 0,01545091. Sustituyendo estos valores y calculando
|
De
…...…..a...……. |
Número de |
Probabilidad |
Número |
(Ni-npi)2/npi |
|
|
exámenes |
del intervalo |
esperado |
|||
|
200 |
250 |
3423 |
0,0223 |
10665,55 |
4918,1271 |
|
250 |
300 |
18434 |
0,0334 |
15984,05 |
375,515279 |
|
300 |
350 |
39913 |
0,0643 |
30732,32 |
2742,54873 |
|
350 |
400 |
51603 |
0,1041 |
49793,4 |
65,7647833 |
|
400 |
450 |
61691 |
0,1422 |
67987,23 |
583,087621 |
|
450 |
500 |
72186 |
0,1636 |
78228,44 |
466,723881 |
|
500 |
550 |
72804 |
0,1586 |
75855,65 |
122,766962 |
|
550 |
600 |
58304 |
0,1296 |
61986,47 |
218,766858 |
|
600 |
650 |
46910 |
0,0893 |
42686,09 |
417,967907 |
|
650 |
700 |
30265 |
0,0518 |
24771,49 |
1218,28167 |
|
700 |
750 |
16246 |
0,0253 |
12113,8 |
1409,55578 |
|
750 |
800 |
6414 |
0,0155 |
7388,52 |
128,535787 |
|
|
|
478193 |
1 |
478193 |
12667,6424 |
Se obtiene que el valor de χ2 con 12 clases es igual a 12.667,64. Por otro lado el valor crítico
![]()
Por tanto la hipótesis nula debe rechazarse. Este ejemplo ilustra el comentario formulado anteriormente con respecto a muestras muy grandes, en las cuales con casi toda seguridad la hipótesis nula será rechazada.
Sea la tabla siguiente en la que se indican el número de anotaciones de 6 puntos en un partido de rugby americano en la temporada de 1979
|
Número de |
Núnero de |
|
0 |
35 |
|
1 |
99 |
|
2 |
104 |
|
3 |
110 |
|
4 |
62 |
|
5 |
25 |
|
6 |
10 |
|
7
ó mas |
3 |
|
|
448 |
Con base en los resultados ajustamos una distribución de Poisson de parámetro la media muestral λ=2,435. ¿Existe alguna razón para creer que a un nivel de 0,05; el número de anotaciones es una variable de Poisson?
Solución
Dado que el valor del parámetro λ no se conoce el estimado de máxima verosimilitud es la media muestral
![]()
Los datos ajustados se muestran en la tabla siguiente:
|
Número de |
Núnero de |
Frecuencia |
Probabilidad |
Número |
(Ni-npi)2/npi |
|
0 |
35 |
0,078125 |
0,08759775 |
39,2437907 |
0,45891997 |
|
1 |
99 |
0,22098214 |
0,21330051 |
95,5586303 |
0,12393465 |
|
2 |
104 |
0,23214286 |
0,25969338 |
116,342632 |
1,30941316 |
|
3 |
110 |
0,24553571 |
0,21078446 |
94,4314366 |
2,56673174 |
|
4 |
62 |
0,13839286 |
0,12831504 |
57,485137 |
0,35459579 |
|
5 |
25 |
0,05580357 |
0,06248942 |
27,9952617 |
0,32046826 |
|
6 |
10 |
0,02232143 |
0,02536029 |
11,3614104 |
0,16313452 |
|
7
ó mas |
3 |
0,00669643 |
0,01245915 |
5,58170083 |
1,19411258 |
|
|
448 |
|
1 |
448 |
6,49131068 |
El valor de χ2=6,491. Para k=8 categorías con un parámetro estimado, el número de grados de libertad es 6. El valor crítico de χ2 0,95; 6 = PRUEBA.CHI.INV(0,05;6)= 12,5915774. Como el valor obtenido 6,491< 12,591 no se puede rechazar la hipótesis nula.
La prueba de bondad de ajuste de Pearson se encuentra limitada cuando F0(x) es continua y la muestra aleatoria disponible es de tamaño pequeño. Una prueba de bondad cuando F0(x) es continua es la de Kolmogorov-Smirnov. No necesita que los datos esten agrupados en intervalos y es aplicable cuando la muestra es pequeña. Ésta se basa en una comparación entre las funciones de distribución acumulativas que se observan en la muestra ordenada y en la distribución propuesta bajo la hipótesis nula.
Consideremos la hipótesis nula H0: F(x)=F0(x), en donde F0(x) se especifica de forma completa. Denótese por x(1), x(2), …, x(n) a las observaciones ordenadas de una muestra aleatoria de tamaño n; y defínase la función de distribución acumulativa muestral como
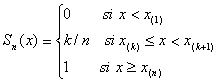
Si la hipótesis nula es correcta las diferencias entre Sn(x) y F0(x) serán pequeñas. El estadístico de Kolmogorov-Smirnov se define como
![]()
El estadístico Dn tiene una distribución que es independiente del modelo propuesto bajo la hipótesis nula, y depende tan solo del tamaño de la muestra. En la tabla adjunta en la hoja de cálculo, se proporcionan valores cuantiles superiores de Dn para varios tamaños de la muestra.
Para un error de tipo I de tamaño a, la región crítica es de la forma
![]()
A continuación se dan los valores ordenados de una muestra aleatoria con las respuestas correctas de los estudiantes que ingresaron en la universidad en la prueba del SAT: 852, 875, 910, 933, 957, 963, 981, 998, 1010, 1015, 1018, 1023, 1035, 1048, 1063. En años anteriores el número de respuestas correctas estaba representado por una N(985; 50). Con base en la muestra, ¿existe alguna razón para creer que ha ocurrido un cambio en la distribución de respuestas correctas en las pruebas del SAT? Empléese un nivel a=0,05.
Solución
|
|
Valores |
Sn(x) |
F0(x) |
|Sn(x)-F0(x)| |
|
1 |
852 |
0,0625 |
0,0039 |
0,0586 |
|
2 |
875 |
0,1250 |
0,0139 |
0,1111 |
|
3 |
910 |
0,1875 |
0,0668 |
0,1207 |
|
4 |
933 |
0,2500 |
0,1492 |
0,1008 |
|
5 |
957 |
0,3125 |
0,2877 |
0,0248 |
|
6 |
963 |
0,3750 |
0,3300 |
0,0450 |
|
7 |
981 |
0,4375 |
0,4681 |
0,0306 |
|
8 |
998 |
0,5000 |
0,6026 |
0,1026 |
|
9 |
1007 |
0,5625 |
0,6700 |
0,1075 |
|
10 |
1010 |
0,6250 |
0,6915 |
0,0665 |
|
11 |
1015 |
0,6875 |
0,7257 |
0,0382 |
|
12 |
1018 |
0,7500 |
0,7454 |
0,0046 |
|
13 |
1023 |
0,8125 |
0,7764 |
0,0361 |
|
14 |
1035 |
0,8750 |
0,8413 |
0,0337 |
|
15 |
1048 |
0,9375 |
0,8962 |
0,0413 |
|
16 |
1063 |
1,0000 |
0,9406 |
0,0594 |
La máxima desviación es 0,1207. El valor crítico para a=0,05 para D16 es 0,328 como puede obtenerse en la hoja adjunta de Excel, como 0,1207<0,328 no puede rechazarse la hipótesis nula.
Muchas veces surge la necesidad de determinar si existe alguna relación entre dos rasgos diferentes en los que una población ha sido clasificada y en donde cada rasgo ha sido subdividido en cierto número de categorías. Cuando una muestra se clasifica de esta manera recibe el nombre de tabla de contingencia de 2 criterios de clasificación. Es posible analizar tablas que contengan más de dos clasificaciones.
El análisis de una tabla de este tipo supone que las dos clasificaciones son independientes. Esto es, bajo la hipótesis nula de independencia se desea saber si existe una diferencia entre las frecuencias que se observan y las correspondientes frecuencias que se esperan. La prueba chi-cuadrada da los medios apropiados.
Sea n una muestra que se clasifica según A y B, cada uno de los cuales tiene r y c categorías. Además, sea Nij el número de observaciones de las categorías i, j de A y B. Se pueden tabular los datos en una matriz de r x c. El total del i-ésimo renglón es la frecuencia de la i-ésima categoría de A, de manera similar para las columnas. Sea
![]()
![]()
Sea pij la probabilidad de que un objeto seleccionado al azar se encuentre en la categoría (i, j), sea pi. la marginal de i de A y p.j la marginal de j de B. Si las características son independientes, la probabilidad conjunta es igual al producto de las marginales
![]()
bajo la hipótesis nula, el estadístico
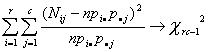
cuando n es grande.
Sin embargo, la mayoría de las veces no se conocen las probabilidades marginales, y de esta forma se estiman con base en una muestra.
Afortunadamente, la prueba de bondad de ajuste de la chi-cuadrado permanece como la estadística apropiada siempre que se empleen los estimados de máxima verosimilitud y se reste un grado de libertad del total para cada parámetro que se esté estimando. Dado que

existen r-1 parámetros de filas y c-1 de columnas a ser estimados.
De esta forma el número de grados de libertad será
rc-1-(r-1)-(c-1)=rc-r-c+1=r(c-1)-(c-1)=(r-1)(c-1)
Puede demostrarse que los estimadores de máxima verosimilitud son
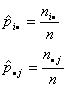
al sustituir se obtiene
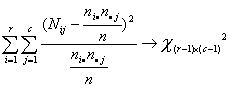
Una compañía evalúa una propuesta para fusionarse con una corporación. El consejo de directores desea muestrear la opinión de los accionistas para determinar si esta es independiente del número de acciones que posee cada uno. Una muestra aleatoria de 250 accionistas da los siguientes resultados:
|
Número de |
Opinión |
|
||
|
acciones |
A favor |
En contra |
Indecisos |
Totales |
|
Menos de 200 |
38 |
29 |
9 |
76 |
|
200-1000 |
30 |
42 |
7 |
79 |
|
Más de 1000 |
32 |
59 |
4 |
95 |
|
|
|
|
|
|
|
Totales |
100 |
130 |
20 |
250 |
Con base en esta información, ¿existe alguna razón para dudar de que la opinión con respecto a la propuesta es independiente del número de acciones que posee el accionista? Úsese a =0,1.
Solución
Formulamos la hipótesis nula de independencia de los dos caracteres; es decir:
H0: pij = pi.p.j
i=1,2,3; j=1,2,3.
Como las probabilidades marginales no se conocen, hay que estimarlas de la muestra, en consecuencia, el estadístico
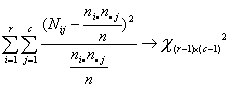
|
Número de |
Opinión |
|
||
|
acciones |
A favor |
En contra |
Indecisos |
Totales |
|
Menos de 200 |
38 |
29 |
9 |
76 |
|
200-1000 |
30 |
42 |
7 |
79 |
|
Más de 1000 |
32 |
59 |
4 |
95 |
|
|
|
|
|
|
|
Totales |
100 |
130 |
20 |
250 |
|
|
|
|
|
|
|
|
|
|
|
Sumas |
|
|
1,9 |
2,80036437 |
1,40236842 |
6,10273279 |
|
|
0,08101266 |
0,0206037 |
0,07316456 |
0,17478092 |
|
|
0,94736842 |
1,86558704 |
1,70526316 |
4,51821862 |
|
|
|
Suma
Total |
10,7957323 |
|
El valor obtenido de la muestra para χ2=10,7957323. El valor crítico que se obtiene en la distribución chi-cuadrado es χ0,9;4= PRUEBA.CHI.INV(0,1;4)= 7,77943396. Como 10,795 > 7,779 el estadístico de prueba se encuentra dentro de la región crítica y por tanto la hipótesis nula debe rechazarse.