Para volver al menú principal pulse sobre la palabra

Distribuciones Estadísticas Bidimensionales.

Esquema

1. Tablas

2. Distribuciones marginales

3. Distribuciones condicionadas

4. Independencia 

5. Dependencia funcional.

6. Caso general

7. Distribuciones marginales y condicionadas. Relaciones entre sus características

8. Media marginal y medias condicionadas

9. Varianza marginal y varianza condicionadas

Características Globales de una distribución de dos variables.

1. Curvas de regresión

2. Razón de correlación

3. Propiedades de la curva de regresión.

4. Recta de mínimos cuadrados.

5. Comparación entre las razones de correlación y el coeficiente de correlación lineal.

Tablas.

Consideremos una población de N individuos descritos simultáneamente según dos caracteres A y B. Designemos por A₁, A₂, …, A_k las modalidades del carácter A y por B₁, B₂, …, B_p las modalidades del carácter B. Sean n_ij el número de individuos de la población que presentan a la vez la modalidad A_i del carácter A y la modalidad B_j del carácter B. Debido a que las modalidades son exhaustivas e incompatibles, se tiene:

La tabla estadística que describe a los individuos, es una tabla de doble entrada, donde figuran en las filas las modalidades de A y en las columnas las de B.

Donde:

[Volver al principio]

Distribuciones Marginales.

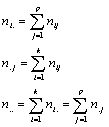
Consideremos  la columna marginal de la tabla de doble entrada. Las frecuencias absolutas n_i. definen lo que se llama distribución marginal según el carácter A. Es una distribución de un solo carácter.

La frecuencia relativa de la modalidad A_i es f_i.= n_i. /N. La suma de las frecuencias relativas marginales es la unidad.

Análogamente se define la distribución marginal del carácter B.

[Volver al principio]

Distribuciones Condicionadas.

Consideremos los n_.j individuos que presentan la modalidad B_j del carácter B. La j-ésima columna de la tabla de doble entrada describe esta subpoblación según el carácter A: n_ij individuos en n_.j presentan la modalidad A_i del carácter A. Se dice también que la frecuencia de la modalidad A_i condicionada por B_j es igual a:

f_i^j=n_ij/n_.j

La tabla estadística de la distribución de A condicionada por B_j tiene la forma siguiente:

Análogamente se define la distribución  condicionada de B por A_i.

[Volver al principio]

Independencia y dependencia funcional.

Definición.

A es independiente de B si las distribuciones condicionadas (A/B_j) son idénticas entre sí, no dependen de j. Por ejemplo:

Se tiene:

Por otra parte, si las fracciones son iguales entre sí, también lo son a la fracción que se obtiene sumando los numeradores y denominadores.

,

de donde f_i^j=f_i..

Así, si A es independiente de B, las distribuciones condicionadas (A/B_j) son idénticas a la distribución marginal de A: las columnas de la tabla de doble entrada son proporcionales entre sí y proporcionales a la columna marginal.

Consideremos por otra parte la relación:

,

de donde se obtiene:

.

Como A es independiente de B, se tiene:

por tanto:

de :

se deduce:

de donde se obtiene:

y por consiguiente B es independiente de A. Es decir, la relación de independencia es recíproca.

Las frecuencias absolutas de las condicionadas son proporcionales a las frecuencias absolutas de las marginales.

[Volver al principio]

Dependencia funcional.

Definición.

A depende funcionalmente de B si a cada modalidad B_j de B corresponde una única modalidad de A. Es decir, para cualquier j es f_ij=0 salvo para un i, i=j(j) donde f_ij=f_.j

Así, en cada columna, un término y solo uno es distinto de cero. La dependencia funcional no es recíproca. Puede haber varios términos no nulos en una misma fila.

Cuando en cada fila y en cada columna figura uno y solo un término de la tabla no nulo, la dependencia es recíproca. Ello requiere que A y B tengan el mismo número de modalidades.

[Volver al principio]

Caso General.

La independencia y dependencia funcional son casos extremos que rara vez se encuentran en la práctica.

Si existe independencia entre A y B, saber que un individuo presenta la modalidad B_j del carácter B no nos dice nada sobre la modalidad A_i de A (Información nula).

Si el carácter A depende funcionalmente de B, el conocimiento de la modalidad B_j permite concluir la modalidad A_i: i=j(j) (Información total).

La práctica se encuentra entre los dos casos extremos : saber que un individuo presenta la modalidad B_j del carácter B nos da un elemento de información que restringe las modalidades posibles o probables de A.

Ejemplo:

Si la población estudiada es el conjunto de los matrimonios celebrados un año dado, descritos según las edades de los esposos ( 25 años por ejemplo), se posee una cierta información sobre la edad de la esposa ( es muy probable que tenga menos de 30 años). La información sería total si los hombres de 25 años se casasen con mujeres de la misma edad; sería nula si la distribución por edad de las esposas de los hombres de 25 años fuera la misma que la correspondiente a los hombres de 20 años, de 30 ó de 50 años.

[Volver al principio]

Distribuciones Marginales y Condicionadas. Relaciones entre sus características.

La distribución marginal de X resulta de la composición de las distribuciones marginales de X / (Y=y_j) representadas por las proporciones f_.j.

La distribución marginal de Y resulta de la composición de las distribuciones condicionadas Y / (X=x_i) representadas por las proporciones f_i..

Por consiguiente son aplicables los resultados ya estudiados para composiciones.

[Volver al principio]

Media marginal y Medias condicionadas.

La media de la composición es igual a la media ponderada por la proporciones de las medias subpoblacionales.

[Volver al principio]

Varianza marginal y varianzas condicionadas.

La varianza de una composición es igual a la media de las varianzas más la varianza de las medias.

[Volver al principio]

Características Globales de una distribución de dos variables.

Curvas de regresión

Se llama curva de regresión de Y sobre X, la curva representativa de las medias condicionadas  en función de los valores x_i. Se trata de una verdadera curva si la variable X es continua o de una sucesión de puntos si la variable es discreta.

donde es la media de la distribución condicionada Y / (X=x_i).

Caso de independencia.

Si las variables X e Y son independientes, las distribuciones condicionadas son idénticas entre sí e idénticas a la distribución marginal correspondiente.

Por consiguiente las curvas de regresión son dos rectas paralelas a los ejes de coordenadas.

Caso de dependencia funcional.

a)      No recíproca.

Supongamos que la variable Y depende funcionalmente de X: a cada valor posible de x_i de X corresponde un único valor  y_i de Y. La media de la variable condicionada Y / (X=x_i) degenerada es igual a y_i. Por consiguiente la curva de regresión de Y sobre X coincide con la curva de dependencia.

(…)

Correlación.

Cuando la curva de regresión de Y sobre X no es paralela al eje de abscisas , se dice que Y está correlada con X.

Observemos que la ausencia de correlación, en general, no es recíproca.

La noción de correlación se refiere exclusivamente a las medias condicionadas. Si por ejemplo se considera una población descrita según el salario y la edad, el salario está incorrelado con la edad, si el salario medio de las personas de 25 años, de las personas de 30 años, etc., es igual al salario medio del conjunto de la población. La independencia de los salarios con la edad se verificaría si la pirámide de los salarios de las personas de 25 años, de las personas de 30, etc., fuesen iguales e idénticos a los de la población global.

La intensidad de la correlación es tanto mayor cuanto más representativa de los valores y_j de Y sea la curva de regresión de Y sobre x, es decir, que los puntos (x_i, y_j ) estén mas concentrados alrededor de la curva de regresión.

El estudio de la correlación de Y sobre x lleva consigo dos nociones:

·         Curva de regresión de Y sobre x.

·         Intensidad de la correlación de Y sobre x.

[Volver al principio]

Razón de Correlación.

La varianza marginal de Y, se puede descomponer en dos sumandos, ambos positivos:

Se llama razón de correlación de Y sobre x, la proporción de la varianza marginal representada por la varianza de las medias condicionadas:

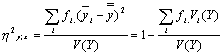
Análogamente, se define la razón de correlación de X sobre y . En general, las dos son diferentes y verifican:

Significado.

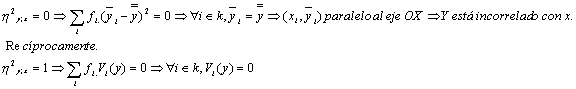
al valor x_i de X corresponde un único valor de y, por consiguiente Y depende funcionalmente de X. Recíprocamente.

Así, pues, la razón h² _y;x  es una medida de la intensidad de la dependencia de Y sobre X .

Análogamente para  h² _x;y .

[Volver al principio]

Propiedades de la curva de regresión.

La curva de regresión de Y sobre X, y=j(x), es la que hace mínima la media – ponderada por las frecuencias – de los cuadrados de las desviaciones tomadas paralelamente al eje de ordenadas entre los diferentes puntos M_ij de coordenadas (x_i; y_j) y la curva y=j(x).

El valor mínimo M es igual:

Análogamente para la curva de regresión de X sobre Y, x=y (y). El valor mínimo alcanzado es:

[Volver al principio]

Recta de mínimos cuadrados.

Si consideramos la recta más próxima a los puntos M_ij medida por la media, ponderada por las frecuencias, de los cuadrados de las desviaciones tomadas paralelamente al eje de ordenadas y la recta; obtenemos, la recta de regresión de Y sobre X.

La recta mas próxima y=ax+b, hará mínima la cantidad:

de donde:

.

Esto expresa que la recta y=ax+b pasa por el centro de gravedad G( ).

de donde se obtiene

Llamando

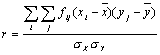
 coeficiente de correlación lineal, que es simétrico respecto de X y de Y, se puede escribir:

De donde se obtiene la recta:

Si permutamos los papeles entre X e Y, obtendremos la recta de mínimos cuadrados de las desviaciones tomadas paralelamente al eje de abscisas:

 El valor mínimo alcanzado es m = (1-r²).V(Y), siendo r² el cuadrado del coeficiente de correlación lineal de X e Y. Coeficiente que es simétrico con respecto a X y a Y.

Análogamente para le recta de regresión de X sobre Y. En este caso el mínimo alcanzado vale: m´= (1-r²).V(X)

  [Volver al principio]

Comparación entre las razones de correlación y el coeficiente de correlación lineal.

Por tanto, se tiene:

(La igualdad entre los mínimos M y m se produce cuando la curva óptima es una recta. Análogamente para M´y m´).

Luego, dividiendo por V(Y) y V(X) respectivamente y operando, se tiene:

Si r=±1, entonces necesariamente

  .

 Se deduce también que  el mínimo m=0 ;(m = (1-r²).V(Y)). Es decir, los puntos M_ij está alineados, por tanto las variables X e Y se corresponden funcionalmente por una dependencia lineal.

Si

entonces necesariamente es r=0.

No se puede obtener nada de la igualdad a 0 de r ni de la igualdad a 1 de las razones de correlación.

  [Volver al principio]