
 |
Para volver al menú principal pulse sobre la palabra |
|---|
Esquema:
El enfoque bayesiano se basa
en la interpretación subjetiva de la probabilidad, el cual considera a ésta
como un grado de creencia con respecto a la incertidumbre.
Un parámetro es visto como
una variable aleatoria a la que, antes de la evidencia muestral, se le asigna
una distribución a priori de probabilidad, con base en un cierto grado de
creencia con respecto al comportamiento aleatorio. Cuando se obtiene la
evidencia muestral, la distribución
a priori es modificada y entonces
surge una distribución a posteriori
de probabilidad.
Dado
que se considera un parámetro como una variable aleatoria, se denomina a éste
con el símbolo Θ y la realización
de esta con el símbolo θ. Supóngase que Θ
es continua con función de densidad (a
priori) incondicional f Θ
(θ), la cual
refleja la creencia a priori con
respecto a la incertidumbre de Θ.
La
información muestral se encuentra representada por n
variables aleatorias IID X1, X2, …, Xn, con
función de densidad condicional f (x | θ),condicional común sobre
la realización de θ de Θ.
La
función de verosimilitud, condicionada a un valor particular de θ, es:
![]()
Mediante
el empleo de teorema de bayes, la función de densidad a
posteriori de Θ dado el resultado muestral
![]()
es
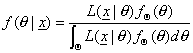
Se
sabe que la densidad a posteriori representa el grado de creencia modificado con respecto
a la incertidumbre de Θ. Pero, ¿cómo debe de usarse la densidad a
posteriori para obtener un estimador puntual de θ? Para este enfoque se
tiene en cuenta lo que se denomina como función de pérdida, que representa la
consecuencia económica de haber escogido a t que es también una función del
resultado muestral, en lugar del verdadero valor θ. Esta función se denota
como l (t, θ) y es no negativa,
valiendo 0 cuando t= θ.
Sea
f Θ (θ)
una función de densidad a priori de
un parámetro Θ, y L (x1, x2, …, xn |
θ) la función de máxima verosimilitud de una muestra aleatoria IID
condicionada a la realización θ de Θ,. Además, sea
f θ |x) la función de densidad a
posteriori de Θ, y sea (l
(t, θ) la función de pérdida. El estimador de Bayes de θ,
T=u(X1, X2, …,Xn) es aquél para el cuál el valor esperado de la función de
pérdida dada por
![]()
es
mínimo.
La
función de pérdida es a veces difícil de especificar , ya que las
consecuencias económicas no son siempre fácilmente medibles. Una función que
suele utilizarse en muchos problemas es:
![]()
Puede
demostrarse que el estimador de Bayes de
θ para esta función es igual a la esperanza a
posteriori E [Θ | x ], de Θ; es decir, la media de la distribución
a posteriori de Θ es el estimador
de Bayes para esta función.
Sea
f (θ|x) la función de densidad a
posteriori de Θ condicionada por el resultado muestral t, sean a y b límites
tales que
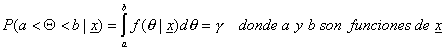
Entonces
el intervalo (a, b) es un intervalo bayesiano tal, que la probabilidad de que
θ se encuentre en (a, b) es γ.
En
este caso, a diferencia de los intervalos de confianza, es un verdadero
intervalo de probabilidad.
Veamos
un ejemplo
Sean
X1, X2, …, Xn la muestra aleatoria de una distribución normal con media
desconocida y varianza σ2 conocida. Supóngase que la media es
un parámetro aleatorio al cuál se piensa asignar una distribución de
probabilidad a priori normal, con una
función de densidad
![]()
μ0
y σ02 son la media y la varianza a
priori. La función de verosimilitud, dada la ocurrencia de μ es:
![]()
Entonces
puede demostrarse que la función de densidad a
posteriori de la media condicionada sobre x también es normal con media
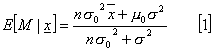
y
varianza
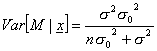
De
esta forma el estimador de Bayes de μ para una función de pérdida
![]()
está
dado por [1]