
 |
Para volver al menú principal pulse sobre la palabra |
|---|
Sea E un espacio muestral y P(E) el algebra de (sucesos) Boole de todos los subconjuntos de E. Sobre P(E) se define la aplicación:
![]() p:
P(E)
R
p:
P(E)
R
Que a cada elemento de P(E) o suceso se le hace corresponder un número real y que verifica:
1. p(A) es no negativo.
2. p(E)=1
3. Si A, B son dos sucesos incompatibles, p(AÈB)=p(A)+p(B).
La terna (E, P(E), p) se llama espacio probabilístico y a p se le llama probabilidad.
1. Si A* es el suceso contrario de A, se verifica que p(A*) = 1 - p(A).
En efecto: como A y A* son contrarios, AÈA*=E, y AÇA*=f. Por tanto p(AÈA*)=p(E)=1, por otra parte p(AÈA*)=p(A)+p(A*), luego p(A*) = 1 - p(A).
2. p(f)=0. En efecto: f=E* y aplicando 1, se tiene que p(f)=1-p(E)=1-1=0.
3. Si A y B son dos sucesos cualesquiera, p(AÈB) = p(A) + p(B) – p(AÇB). La demostración es la siguiente: A=(A-B)È(AÇB) y B=(B-A)È(AÇB) y AÈB=(A-B)È(B-A)È(AÇB) estos tres conjuntos han sido descompuestos en unión de conjuntos disjuntos y por tanto se les puede aplicar a cada uno el axioma 3. Despejando p(A-B) y p(B-A) en el 1º y 2º y sustituyendo en el 3º queda demostrado el teorema.
Para explicar la probabilidad condicionada consideremos el siguiente ejemplo. Extraigamos dos bolas de una urna que contiene 3 bolas blancas y 2 bolas negras. En el primer caso, la extracción se hace de una bola y a continuación la otra y sin devolución; y, en el 2º con devolución. En el primer caso, el resultado de la extracción de la segunda bola depende del resultado obtenido en la 1ª. En el 2º caso el resultado de la extracción de la 2ª bola es independiente del resultado obtenido en la 1ª. Este ejemplo nos sirve para definir la probabilidad de A condicionada a B, que se define como la probabilidad de ocurrencia de A, en el supuesto de que ya ha ocurrido B:
![]() .
.
Análogamente se define la probabilidad de
![]()
De la definición se deduce que
![]() .
.
Cuando A y B son independientes, la ocurrencia de uno de ellos no influye para nada en la ocurrencia del otro suceso. Se define la independencia de A y B cuando p(A/B)=p(A) ó p(B/A)=p(B), en cualquier caso p(AÇB)=p(A).p(B). Esta última igualdad suele tomarse como definición de independencia.
Sea {Ai; i=1,2,…,k }un sistema completo de sucesos y B un suceso cualquiera del espacio muestral E. Se tiene que la p(B)=p(B/A1)p(A1)+p(B/A2)p(A2)+…+p(B/Ak)p(Ak).
Demostración:
![]()
El teorema de Bayes se basa en la doble igualdad
![]()
y en el supuesto del conocimiento de todas las probabilidades condicionadas de B con los sucesos del sistema completo {Ai; i=1,2,…,k }, en tales condiciones es posible deducir la p(Ai/B). Es decir, en el supuesto de que se ha realizado B, ¿Cuál es la probabilidad de que también se haya realizado Ai?
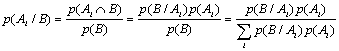 .
.